本記事では、ESPRIT(Estimation of Signal Parameter via Rotation Invariance Techniques)法による音源定位を試してみました。ESPRIT法は Roy et al により提案された2組のセンサアレイを用いた到来方向推定法となります[1]。
ESPRIT法のアレイ配置
ESPRIT法では2組のセンサアレイ間の位相差を利用して到来方向を推定します。下図のようにペアとなるセンサ間の距離を \(\Delta d\) で一定として、ペアどうしのセンサの感度は同じとなるようにします。
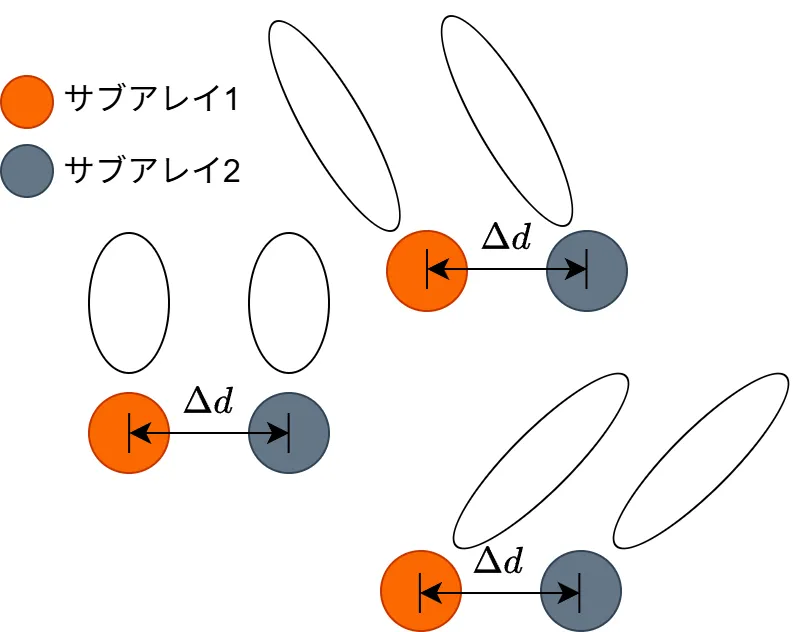
このように、ESPRIT法はセンサの位置に制約があり、他の方法と比較してセンサの個数が2倍必要であったり、設計が困難になったりして、一般的にコストが高くなります。
そのため、下図のようにM素子の直線状等間隔アレイ(ULA)を、Ms素子の2つのサブアレイに分割して代用するやり方がしばしば使われます。
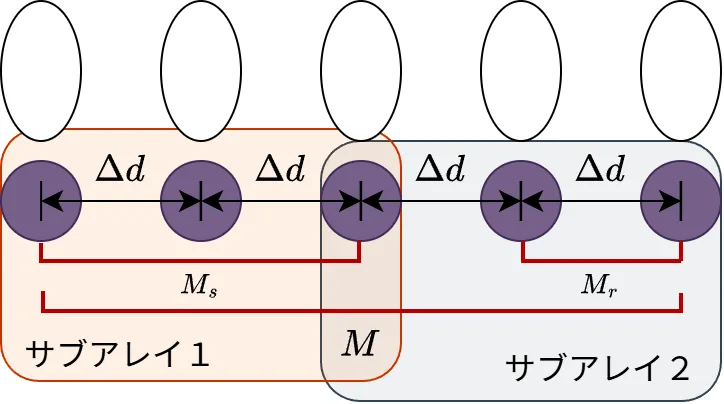
これならば、センサの個数は2倍も必要なく、センサの位置も気をつける必要がないです。
補足:\(\Delta d\ \)については大きすぎると位相が半周期違くなり、信号の到来方向の推定を誤ります(下図だと位相が同じ(1周期ずれ)で0度方向と間違える)。
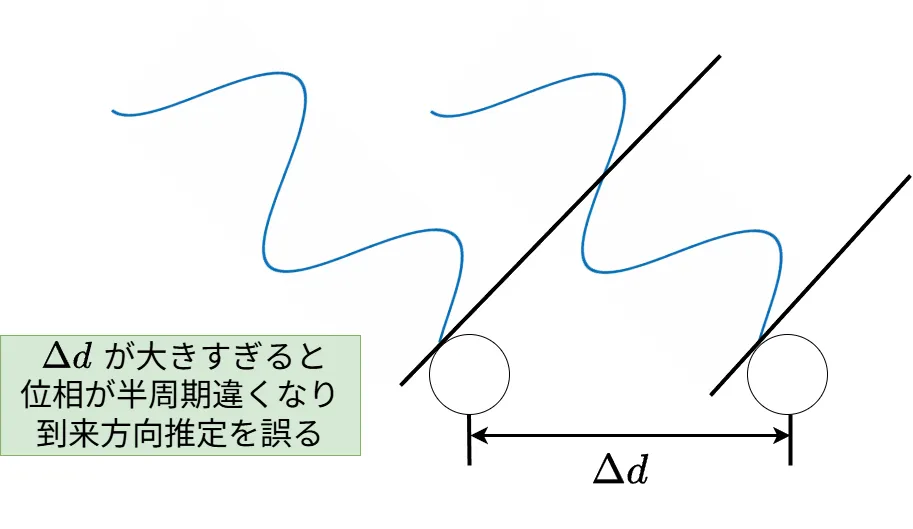
位相が半周期より異なると到来方向を誤るので、センサ間隔 \(\Delta d\) の条件は以下になります。\(\lambda\ \)は波長です。
$$
\Delta d \leq \frac{\lambda}{2}
$$
部分空間法
ESPRIT法について解説する前に、前提知識である部分空間法について説明します。主成分分析の記事で詳しく解説していますが、時間も経っているので簡単に解説します。
信号モデル
観測信号の短時間フーリエ変換 \(\ X_{m}[l,k]\ \) を以下のように表せると考えます。
$$
\begin{equation}
\begin{bmatrix}
X_{1}[l,k] \\
\vdots \\
X_{m}[l,k] \\
\vdots \\
X_{M}[l,k]
\end{bmatrix}
= {\mathbf A}[k]
\begin{bmatrix}
S_{1}[l,k] \\
\vdots \\
S_{i}[l,k] \\
\vdots \\
S_{N}[l,k]
\end{bmatrix}
+
\begin{bmatrix}
N_{1}[l,k] \\
\vdots \\
N_{m}[l,k] \\
\vdots \\
N_{M}[l,k]
\end{bmatrix} \tag{1}
\end{equation}
$$
ここで、\(l\ \)はフレーム番号、\(k\ \) は周波数ビン番号、\(m\ \)は観測信号のインデックス、\(i\ \)は音源信号のインデックス、\(S_{i}[l,k]\ \)は音源信号を短時間フーリエ変換した結果、\(N_{m}[l,k]\ \)はノイズを短時間フーリエ変換した結果です。
また、\(\ {\mathbf A}[k]\ \)はアレイマニフォールド行列と呼ばれ、要素 \(\ a_{mi}[k]\ \)が音源\(\ i\ \)からセンサ\(\ m\ \)までの経路の伝達関数となっております。
\begin{align}
{\mathbf A}[k] &=
\begin{bmatrix}
{\mathbf a}_{1}[k] & \cdots & {\mathbf a}_{i}[k] & \cdots & {\mathbf a}_{N}[k] \end{bmatrix} \tag{2} \\[10pt] {\mathbf a}_{i}[k] &=
\begin{bmatrix}
a_{1i}[k] & \cdots & a_{mi}[k] & \cdots & a_{Mi}[k] \end{bmatrix}^{T} \tag{3}
\end{align}
$$
アレイマニフォールド行列の列ベクトル \(\ {\mathbf a}_{i}[k]\ \)はアレイマニフォールドベクトルとよばれ、音源 \(i\) からの音波の到来方向を表す情報になります。
部分空間法について
\(l, k\ \)の添え字を省略して、観測信号を以下のように表します。
$$
{\mathbf X}=
\begin{bmatrix}
X_{1} & \cdots & X_{m} & \cdots & X_{M}
\end{bmatrix}^{T} \tag{4}
$$
観測信号から以下の空間相関行列を計算します。
$$
{\mathbf R}=E[{\mathbf X}{\mathbf X}^{H}] \tag{5}
$$
ここで、\(E[\cdot]\ \)は期待値演算、\(\{\cdot\}\ \)はエルミート転置です。
期待値演算については一般的に以下の時間平均で計算されます。
$$
{\mathbf R}[k]=\frac{1}{L}\sum_{l=0}^{L-1} {\mathbf X}[l,k]{\mathbf X}^{H}[l,k] \tag{6}
$$
空間相関行列を固有値分解して固有値 \(\ \mu_{m}\ \)と固有ベクトル\(\ {\mathbf e}_{m}\ \)を求めます。
$$
\mu_{m} = {\mathbf e}_{m}^{-1} {\mathbf R}[k] {\mathbf e}_{m} \tag{7}
$$
それから固有値の大きい順に固有ベクトルを並べ替え、音源の数だけ取り出した固有ベクトルを\(\ {\mathbf E}_{s}=\{{\mathbf e}_{1},\cdots, {\mathbf e}_{N}\}\ \)とします
このとき、アレイマニフォールドベクトル\(\ \{{\mathbf a}_{1},\cdots, {\mathbf a}_{N}\}\ \)と固有ベクトル\(\ \{{\mathbf e}_{1},\cdots, {\mathbf e}_{N}\}\ \)の幾何学的関係は以下のように表されます。
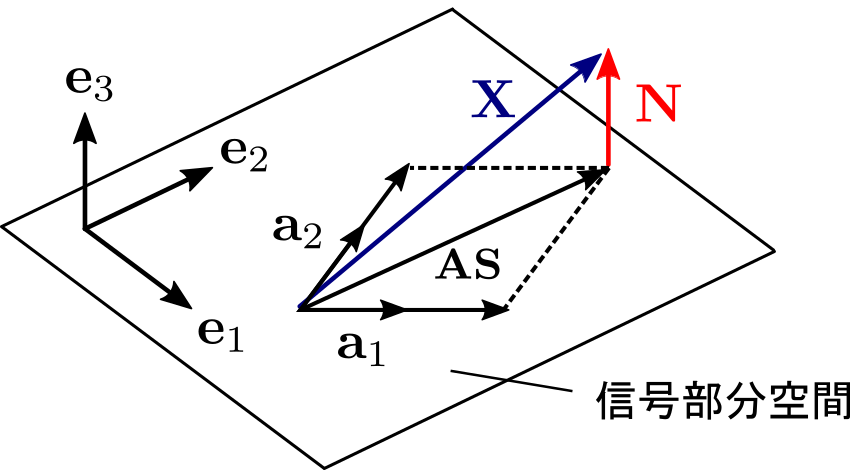
アレイマニフォールドベクトルによって張られる空間は信号部分空間と呼ばれます。音源の数 N=2 のとき、空間相関行列の固有ベクトル \({\mathbf e}_{1}\), \({\mathbf e}_{2}\) については信号部分空間の正規直交基底となっています。
つまり、\({\mathbf E}_{s}\ \)がわかれば、アレイマニフォールドベクトルがだいたいわかるということです。
ESPRIT法の詳解
サブアレイ間の位相差
センサアレイの配置を直線上等間隔アレイとすると、アレイマニフォールド行列\(\ {\mathbf A}\ \)の要素 \(a_{mi}\ \)は以下のように表されます(参照:ビームフォーミングで特定方向の音源を強調)。
$$
\begin{align}
a_{mi} &= \exp\left(j\left\{(m-1)-\frac{M-1}{2}\right\} \psi_{i}\right) \tag{8}\\[5pt]
\psi_{i} &= \frac{2\pi d}{\lambda} \sin{\theta_{i}} \tag{9}
\end{align}
$$
補足:ULAのアレイマニフォールドベクトルが参照の記事と違うのは以下のようにしているためです。
・以下のように式変形して、波長 \(\lambda\ \)を使って表している
$$
\lambda = \frac{c}{(k/N) f_{s}}
$$
・今回、到来方向 \(\theta_{i}\ \)が時計回りを正とした。
なるべく、参考文献と同じ表記にするために変更してます。
また、サブアレイのアレイマニフォールド行列の \({\mathbf A_{1}}\), \({\mathbf A_{2}}\ \)は\(\ {\mathbf A}\ \)を使って以下のように表されます。
$$
\begin{align}
{\mathbf A_{1}} &= {\mathbf J}_{1}{\mathbf A} \tag{10} \\[5pt]
{\mathbf A_{2}} &= {\mathbf J}_{2}{\mathbf A} \tag{11}
\end{align}
$$
ここで、\({\mathbf J}_{1}\)、\({\mathbf J}_{2}\)はサブアレイ選択行列で以下のように表されます。\( {\mathbf I}\ \)は単位行列です。
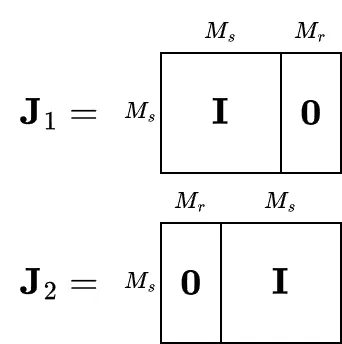
例えば、\(M=7\ \), \(M_{r}=1\)とすると、 \({\mathbf A_{1}}\), \({\mathbf A_{2}}\ \)は以下のようになります。
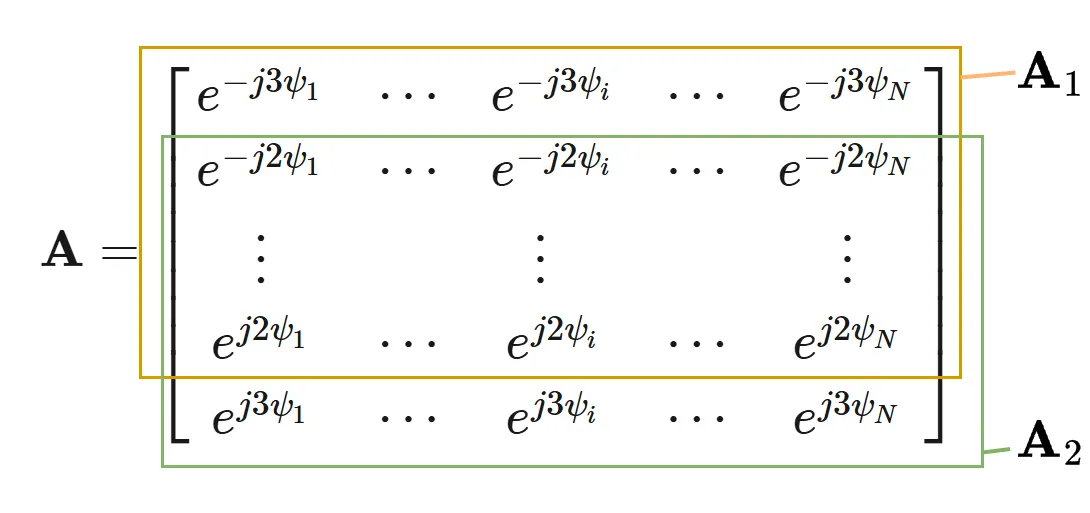
上図から、\({\mathbf A_{1}}\), \({\mathbf A_{2}}\ \)の関係式は以下のようになり、
$$
\begin{equation}
{\mathbf A_{2}} = {\mathbf A_{1}}{\mathbf \Phi} \tag{12}
\end{equation}
$$
$$
\begin{equation}
{\mathbf \Phi} =
\begin{bmatrix}
e^{jM_{r}\psi_{1}} & & & O \\
& e^{jM_{r}\psi_{2}} & & \\
& & \ddots & \\
O & & & e^{jM_{r}\psi_{N}}
\end{bmatrix} \tag{13}
\end{equation}
$$
\({\mathbf \Phi}\ \)を求めれば、サブアレイ間の位相差から到来方向を推定できます。
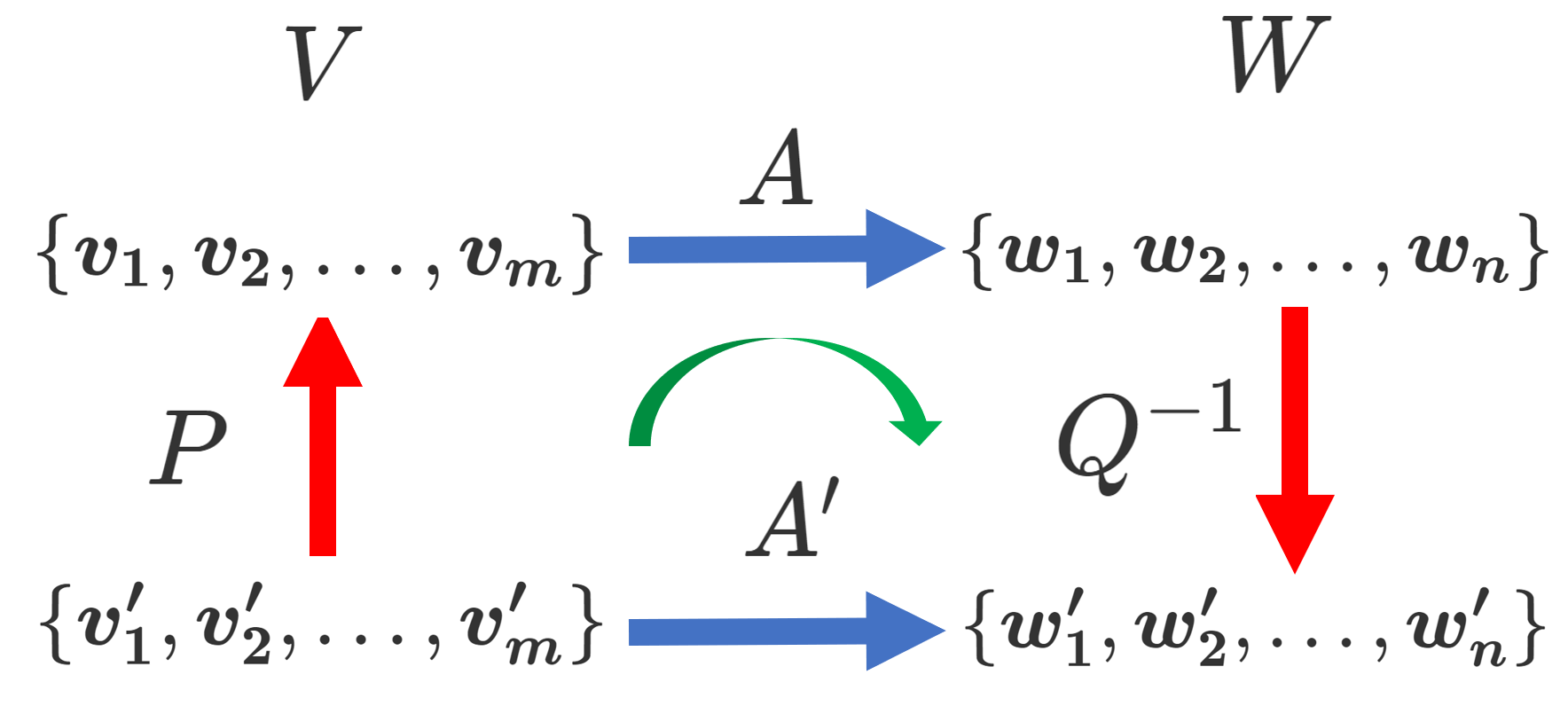
\({\mathbf E}_{s}\ \)を使った位相差の関係式
アレイマニフォールドベクトルは信号部分空間を張り、空間相関行列の固有ベクトル \({\mathbf E}_{s}=[{\mathbf e}_{1},\cdots, {\mathbf e}_{N}]\ \) は信号部分空間の正規直行基底となります。このことから、\(\mathbf A\) と\(\ {\mathbf E_{s}}\ \)の間には、以下のような変換を行うNxN の正則行列\(\ {\mathbf T}\ \)が存在します。
$$
\begin{equation}
{\mathbf A} = {\mathbf E}_{s}{\mathbf T} \tag{14}
\end{equation}
$$
変換行列については以下のブログの解説がわかりやすいです。
式に サブアレイ選択行列 \({\mathbf J}_{1}、{\mathbf J}_{2}\ \)をかけると、
$$
\begin{align}
{\mathbf A_{1}} &= {\mathbf J}_{1}{\mathbf E}_{s} {\mathbf T} \tag{15}\\[5pt]
{\mathbf A_{2}} &= {\mathbf J}_{2}{\mathbf E}_{s} {\mathbf T} \tag{16}
\end{align}
$$
となり、\({\mathbf E}_{s1}={\mathbf J}_{1}{\mathbf E}_{s}\)、\({\mathbf E}_{s2}={\mathbf J}_{2}{\mathbf E}_{s}\) とおくと
$$
\begin{align}
{\mathbf A_{1}} &= {\mathbf E}_{s1} {\mathbf T} \tag{17}\\[5pt]
{\mathbf A_{2}} &= {\mathbf E}_{s2} {\mathbf T} \tag{18}\\[5pt]
\end{align}
$$
上記の式から、
$$
\begin{align}
{\mathbf E}_{s2} &= {\mathbf A_{2}} {\mathbf T}^{-1} \\[5pt]
&= {\mathbf A_{1}}{\mathbf \Phi}{\mathbf T}^{-1} \\[5pt]
&= {\mathbf E_{s1}}{\mathbf T}{\mathbf \Phi}{\mathbf T}^{-1} \tag{19}
\end{align}
$$
ここで、
$$
{\mathbf \Upsilon}={\mathbf T}{\mathbf \Phi}{\mathbf T}^{-1} \tag{20}
$$
とおくと、
$$
\begin{equation}
{\mathbf E}_{s1} {\mathbf \Upsilon} = {\mathbf E}_{s2} \tag{21}
\end{equation}
$$
となります。
最小2乗法による解法
(21)式から\(\ {\mathbf \Upsilon}\ \)を計算して、\({\mathbf \Phi}\ \)を求めたいのですが、\(\ {\mathbf E}_{s1}\ \)は Ms x N 行列のため、逆行列を計算できません。
そこで、以下の式を最小化する \({\mathbf \Upsilon}\ \)を求めます。
$$
||{\mathbf E}_{s1}{\mathbf \Upsilon} - {\mathbf E}_{s2}||_{F} \tag{22}
$$
\(||\cdot||_{F}\ \)はフロベニウスノルムとなります。
これを最小化する行列は知られており、以下のように表されます。
$$
\begin{equation}
{\hat {\mathbf \Upsilon}} = ({\mathbf E}_{s1}^{H}{\mathbf E}_{s1})^{-1}{\mathbf E}_{s1}^{H}{\mathbf E}_{s2} \tag{23}
\end{equation}
$$
複素数ではないですが、実数の場合の最小二乗法については以下のブログに解説があります(求めるのがベクトルである点も違う)。
(20)式から
$$
{\mathbf \Phi}={\mathbf T}^{-1}{\mathbf \Upsilon}{\mathbf T} \tag{24}
$$
であり、\({\mathbf \Phi}\ \)は対角行列であることから、\({\mathbf \Phi}\ \)の対角成分は\(\ {\mathbf \Upsilon} \ \)の固有値となります。
このことは以下のブログに説明があります。
対角化された行列の対角成分が、もとの行列の固有値であることを証明するページです。…
したがって、\({\mathbf \Upsilon}\ \)の固有値を \(\{{\hat \xi_{1}}, \cdots, {\hat \xi_{N}}\}\) とすると、
$$
\begin{equation}
{\hat \xi_{n}} = \exp(j M_{r} \psi_{n}) \tag{25}
\end{equation}
$$
となり、両辺の位相を抽出すると、
$$
\begin{align}
\arg{\hat \xi_{n}} &= M_{r} \psi_{n} \\[5pt]
&= \frac{2\pi M_{r} d}{\lambda}\sin{\theta_{n}} \tag{26}
\end{align}
$$
\(\theta_{n}\ \)について解くと
$$
\begin{equation}
\theta_{n} = \sin^{-1}\left(\frac{\lambda}{2\pi M_{r}d} \arg{\hat \xi_{n}}\right) \tag{27}
\end{equation}
$$
で到来方向を求めることができます。
プログラム
ソースコード
ESPRIT法をPythonで実装しました。Pythonのソースコード esprit.py は以下となります。
import numpy as np
import soundfile as sf
import scipy.signal as sg
def esprit(X_stft, n_src, d, wavespeed, fs, k_l, k_u):
"""
ESPRIT algorithm
Parameters
----------
X_stft : ndarray (n_mic, n_bin, n_frame)
Observed signal matrix
n_mic: number of sensors
n_bin: number of bins
n_frame: number of frames
n_src : int
Number of sources
d : float
Sensor spacing [m]
wavespeed : float
Wavespeed of signal [m/s]
fs : int
sampling frequency [Hz]
k_l : int
Lower frequency bin index for DOA estimation
k_u : int
Upper frequency bin index for DOA estimation
Returns
-------
doa : ndarray (K,)
Estimated DOAs [rad]
"""
n_mic, n_bin, n_frame = X_stft.shape
# --- 1. パワーが最大である周波数ビンを求める ---
tmp = np.sum(np.abs(X_stft[0,k_l:k_u,:]), axis=1)
bin_powmax = k_l + np.argmax(tmp)
X_stft = X_stft[:,bin_powmax,:]
# --- 2. 波長を求める ---
freq_powmax = (fs/2) * (bin_powmax/(n_bin-1))
print(f"Max power frequency: {freq_powmax} Hz")
wavelength = wavespeed / freq_powmax
print(f"wavelength: {wavelength} m")
# --- 3. 空間相関行列を求める ---
XH_stft = np.conjugate(X_stft)
tmp = np.einsum("mi,ni->mni", X_stft, XH_stft)
R = np.mean(tmp, axis=2)
# --- 4. 信号部分空間を求める ---
eig_vals, eig_vecs = np.linalg.eig(R) # 固有値分解
idx = np.argsort(np.abs(eig_vals))[::-1]
Es = eig_vecs[:, idx[:n_src]]
# --- 5. Es1, Es2を求める ---
Es1 = Es[:-1,:] # upper subarray
Es2 = Es[1:,:] # lower subarray
# --- 6. 最小二乗法を解く ---
Ups = np.linalg.pinv(Es1) @ Es2
# --- 7. Υ(Ups)の固有値 ---
eigvals_Ups = np.linalg.eigvals(Ups)
# --- 8. DOA 推定 ---
xi = np.angle(eigvals_Ups)
phase = np.arcsin(xi * wavelength / (2 * np.pi * d))
if np.any(np.isnan(phase)):
raise ValueError("NaNが含まれています!")
return phase
# パラメータ
N_fft = 512
freq_l = 1500
freq_u = 10000
dir_name = "mic/"
n_mic = 8
n_src = 3
d = 0.03 # [m]
wavespeed = 343 # [m/s]
# 変数初期化
wav_path = dir_name+"mic0.wav"
data, fs = sf.read(wav_path)
x=np.zeros((n_mic,len(data)))
# WAVファイルを読み込む
for i in range( n_mic ):
wav_path = dir_name+"mic"+str(i)+".wav"
data, fs = sf.read(wav_path)
x[i,:] = data
# 周波数ビンに変換
k_l = int(freq_l/(fs/N_fft))
k_u = int(freq_u/(fs/N_fft))
# 窓関数作成
win = sg.windows.hann(N_fft) # ハン窓作成
# 短時間フーリエ変換
SFT = sg.ShortTimeFFT(win, hop=N_fft//2, fs=fs)
X_stft = SFT.stft(x)
print(X_stft.shape)
# ESPRITで音源定位
theta_rad = esprit(X_stft, n_src, d, wavespeed, fs, k_l, k_u)
# rad -> deg
theta_deg = np.rad2deg(theta_rad)
# 角度を出力
for i in range(n_src):
print(f"src{i}: {theta_deg[i]:6.2f} [deg]")
ソースコード解説
● DOA推定に使用する周波数ビンの決定
# --- 1. パワーが最大である周波数ビンを求める ---
tmp = np.sum(np.abs(X_stft[0,k_l:k_u,:]), axis=1)
bin_powmax = k_l + np.argmax(tmp)
X_stft = X_stft[:,bin_powmax,:]
DOA推定に使用する周波数ビンについては、最もパワーが大きい周波数ビンを使用しました。
● 波長を求める
# --- 2. 波長を求める ---
freq_powmax = (fs/2) * (bin_powmax/(n_bin-1))
print(f"Max power frequency: {freq_powmax} Hz")
wavelength = wavespeed / freq_powmax
print(f"wavelength: {wavelength} m")
最大パワーの周波数ビン番号から周波数を求めて、周波数から波長を計算しています。
● 空間相関行列を求める
# --- 3. 空間相関行列を求める ---
XH_stft = np.conjugate(X_stft)
tmp = np.einsum("mi,ni->mni", X_stft, XH_stft)
R = np.mean(tmp, axis=2)
einsum(アインシュタインの縮約記法)を使って行列積を計算したのち、時間軸で平均をとって空間相関行列を計算しています。
● 信号部分空間を求める
# --- 4. 信号部分空間を求める ---
eig_vals, eig_vecs = np.linalg.eig(R) # 固有値分解
idx = np.argsort(np.abs(eig_vals))[::-1]
Es = eig_vecs[:, idx[:n_src]]
固有値分解を行った後、固有値の大きい順に並べ替えたときのインデックスを求めています。そのインデックスをつかって、固有値の大きい固有ベクトルを音源の数だけ取り出して、信号部分空間を求めています。
● \({\mathbf E}_{s1}\),\({\mathbf E}_{s2}\ \)を求める
# --- 5. Es1, Es2を求める ---
Es1 = Es[:-1,:] # upper subarray
Es2 = Es[1:,:] # lower subarray
ここで、\({\mathbf E}_{s1}\),\({\mathbf E}_{s2}\ \)を求めています。
● 到来方向を推定
# --- 6. 最小二乗法を解く ---
Ups = np.linalg.pinv(Es1) @ Es2
# --- 7. Υ(Ups)の固有値 ---
eigvals_Ups = np.linalg.eigvals(Ups)
# --- 8. DOA 推定 ---
xi = np.angle(eigvals_Ups)
phase = np.arcsin(xi * wavelength / (2 * np.pi * d))
if np.any(np.isnan(phase)):
raise ValueError("NaNが含まれています!")
np.linalg.pinv(Es1) で以下の \({\mathbf E}_{s1}\ \)の逆行列を計算して、\({\mathbf \Upsilon}\ \)を求めています。
$$
\begin{equation}
({\mathbf E}_{s1}^{H}{\mathbf E}_{s1})^{-1}{\mathbf E}_{s1}^{H} \tag{28}
\end{equation}
$$
その後、\({\mathbf \Upsilon}\ \)の固有値を計算して、到来方向を求めています。
シミュレーション実験
室内音響シミュレーション(PyRoomAcoustics)で作成した音に対してESPRIT法を使用して、ESPRIT法の音源定位の精度を確かめました。
実験方法
室内音響シミュレーションで図のように音源とマイクを配置して、マイクで音声データを録音しました。
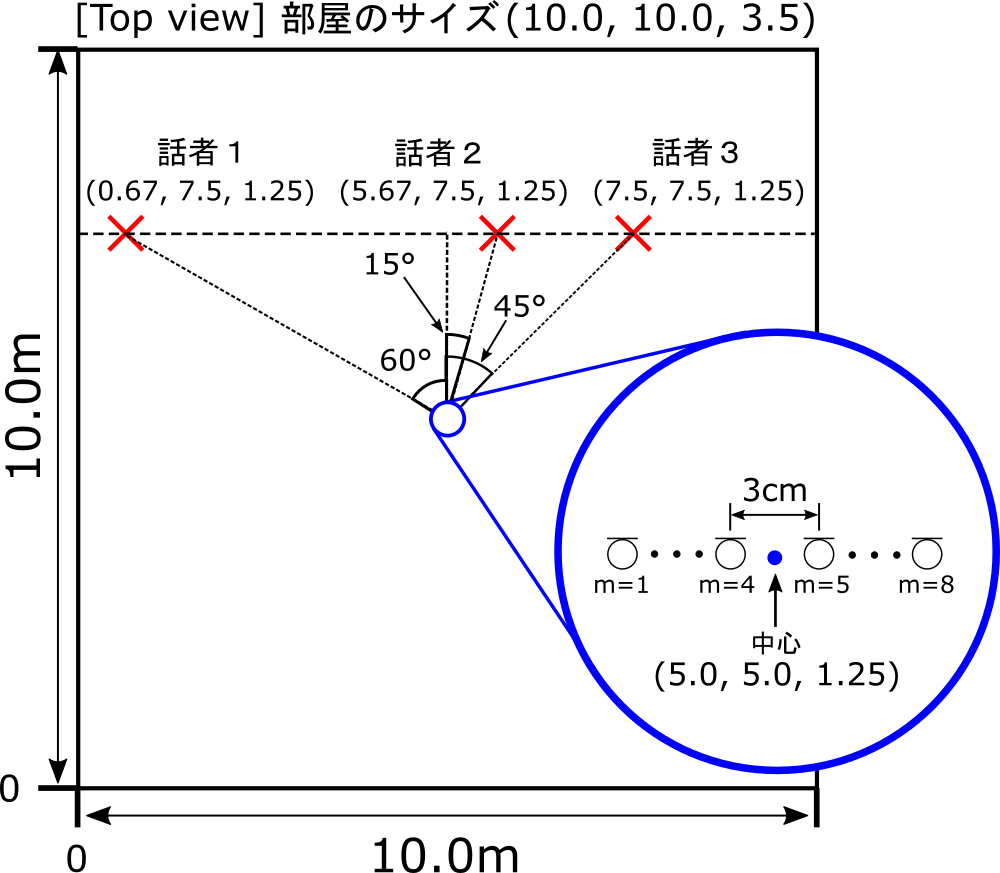
シミュレーションに用いたPythonのコード room_sim.py が以下です(クリックで展開)。
room_sim.py(クリックで展開)
import numpy as np
import pyroomacoustics as pra
import soundfile as sf
from resampy import resample
from math import tan
fs = 16000 # リサンプリング後の周波数
rt60_tgt = 0.2 # 残響時間
room_size = [10, 10, 3.5] # 部屋の大きさ
SNR = 90 # SN比
dir_src = "src/" # 音源のフォルダ
dir_mic = "mic/" # 録音したデータのフォルダ
src_list = ["src1.wav", "src2.wav", "src3.wav"]
# 音源とマイクの位置を決定
center = [5.0,5.0] # 中心の位置
n_src = 3 # 音源の数
n_mic = 8 # マイクの数
d = 0.03 # マイクの間隔 [m]
pos = np.array([-60, 15, 45]) # マイク位置 [deg]
pos = np.deg2rad(pos)
# 音源を配置
s_locs = np.zeros((3,3))
s_locs[:,0] = [5+2.5*tan(pos[0]), 7.5, 1.25]
s_locs[:,1] = [5+2.5*tan(pos[1]), 7.5, 1.25]
s_locs[:,2] = [5+2.5*tan(pos[2]), 7.5, 1.25]
# マイクを線状アレイで配置
m_locs = pra.linear_2D_array(center, n_mic, 0, d)
m_locs = np.insert(m_locs, 2, 1.25, axis=0)
# WAVファイルを読み込む
audio = []
for i, src_name in enumerate(src_list):
x, fs_tmp = sf.read(dir_src+src_name)
x = resample(x, fs_tmp, fs)
audio.append(x)
audio = np.array(audio)
# 残響時間と部屋の大きさから吸音率と反射回数を決定
e_absorption, max_order = pra.inverse_sabine(rt60_tgt, room_size)
# 部屋の作成
room = pra.ShoeBox(
room_size, fs=fs, materials=pra.Material(e_absorption), max_order=max_order
)
# 部屋に音源を配置
for i in range(n_src):
room.add_source(s_locs[:,i], signal=audio[i,:], delay=0)
# 部屋にマイクを配置
room.add_microphone_array(
pra.MicrophoneArray(m_locs, fs=fs)
)
# 部屋をプロットする
fig, ax = room.plot()
ax.set_zlim(0,room_size[2])
fig.savefig("room.png")
# シミュレーションする
room.simulate(snr=SNR)
# マイクで録音した音を書き出す
mic_data = room.mic_array.signals
mic_data = mic_data/np.max(np.abs(mic_data)) # ノーマライズ
for i in range(n_mic):
name = dir_mic+"mic"+str(i)+".wav"
sf.write(name, mic_data[i,:], fs, subtype='PCM_16')
残響時間は0.2秒、収録時のサンプリング周波数は16kHz、SN比は90dB(ほとんど雑音なし)に設定しました。
シミュレーションが出力したマイクと音源の位置は以下です(マイクが並んでいるのがわかるように出力画像はマイク間隔を広げています)。
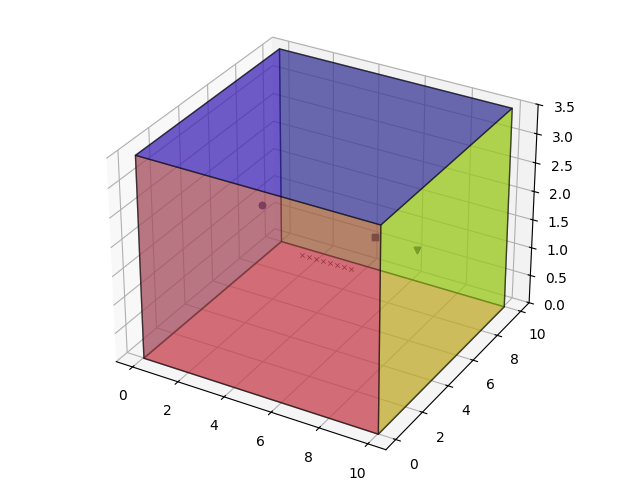
話者1~3の音声とマイク(m=1)で録音した音声は以下になります。
話者1
話者2
話者3
録音信号(m=1)
ESPRITのソースコードを実行したときのパラメータ設定は以下です。
| パラメータ | 変数名 | 値 |
|---|---|---|
| FFT点数 | N_FFT | 512点 |
| 窓関数 | win | ハン窓 |
| 使用する周波数下限 | freq_l | 1.5 kHz |
| 使用する周波数上限 | freq_u | 10 kHz |
| マイクの個数 | n_mic | 8個 |
| 音源の個数 | n_src | 3個 |
| マイク間の距離 | d | 0.03 m |
| 音速 | wavespeed | 343 m/s |
実験結果
ESPRIT法で到来方向を推定した結果は以下でした。時計回りを正の値としてます(MUSIC法の記事では反時計回りが正の値としてました)。
| 音源 | 推定 | 正解 |
|---|---|---|
| 話者1 | \(-62.10\) 度 | \(-60.0\) 度 |
| 話者2 | \(4.23\) 度 | \(15.0\) 度 |
| 話者3 | \(39.68\) 度 | \(45.0\) 度 |
話者2の推定結果については10度くらいずれていますが、他の音源については上手く推定できてます。
プログラムの出力表示は以下でした。話者の番号と出力結果の順序は異なってます。

補足:話者1の方向を-30度、話者2の方向を15度、話者3の方向を30度としたとき、推定結果がどうなるかも見てみました。
推定結果は以下のようになりました。
| 音源 | 推定 | 正解 |
|---|---|---|
| 話者1 | \(-26.97\) 度 | \(-30\) 度 |
| 話者2 | \(10.76\) 度 | \(15\) 度 |
| 話者3 | \(28.28\) 度 | \(30\) 度 |
音源どうしの方向が近い場合、MUSIC法の記事ではうまくいきませんでしたが、ESPRIT法は比較的うまくいきました。MUSIC法の記事の実装が間違ってたのかな?今度確かめてみます。
おわりに
本記事では、ESPRIT法を使用した音源定位を行いました。ESPRIT法はセンサの配置に制約があるため、実際に使うのは難しいのでは?という印象でしたが、直線状アレイの配置をすれば、意外に実環境でも使えそうだなと思いました。
参考文献
[1] 浅野太、”音のアレイ信号処理 音源の定位・追跡と分離”、コロナ社、2011.