本記事では、音声・音響処理で使われている主成分分析 (PCA: Principal Component Analysis)を紹介します。自分が知る限り、主成分分析はアレイ信号処理によく使われています。
主成分分析
まず、主成分分析の概要と主成分の求め方を説明いたします。それから主成分の求め方の詳細について説明していこうと思います。
主成分分析とは
主成分分析では図のようにx1とx2の散布図があるときw1のような新しい軸(変数)を作ります。
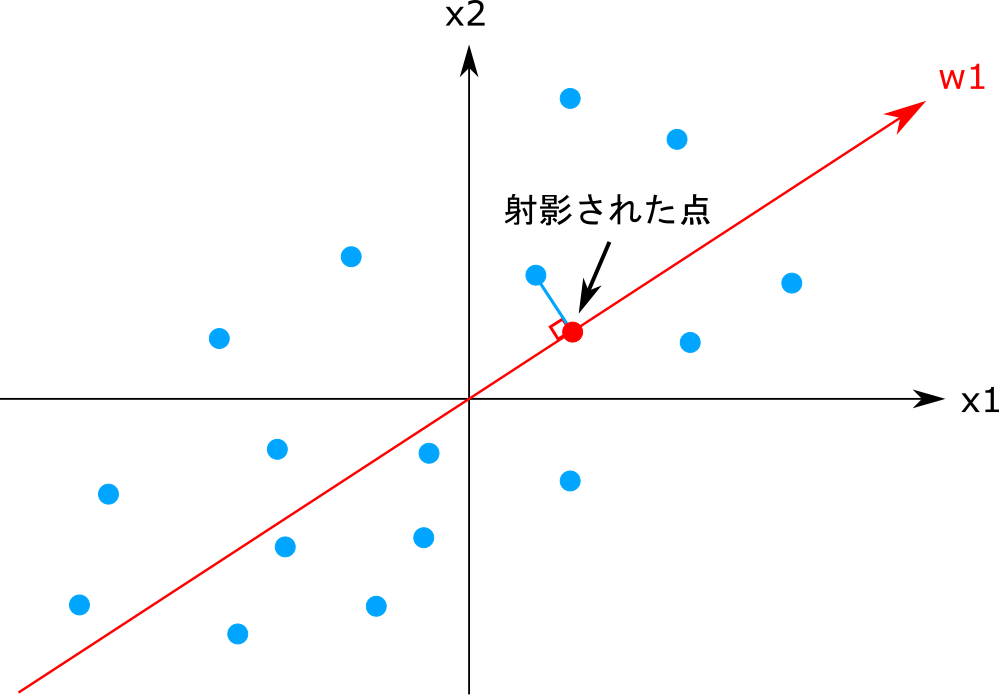
w1の軸は、データを軸に射影したとき、その成分の分散が最大となるように決定します。このw1の軸は第1主成分と呼びます。
第2主成分、第3主成分、・・・については、これまでに決定した主成分と直交して、かつ射影した成分の分散が最大となるように決定します。x1 と x2 の場合、直交する軸は一つしかないので、自動的に第2主成分 w2 が図のように決定します。
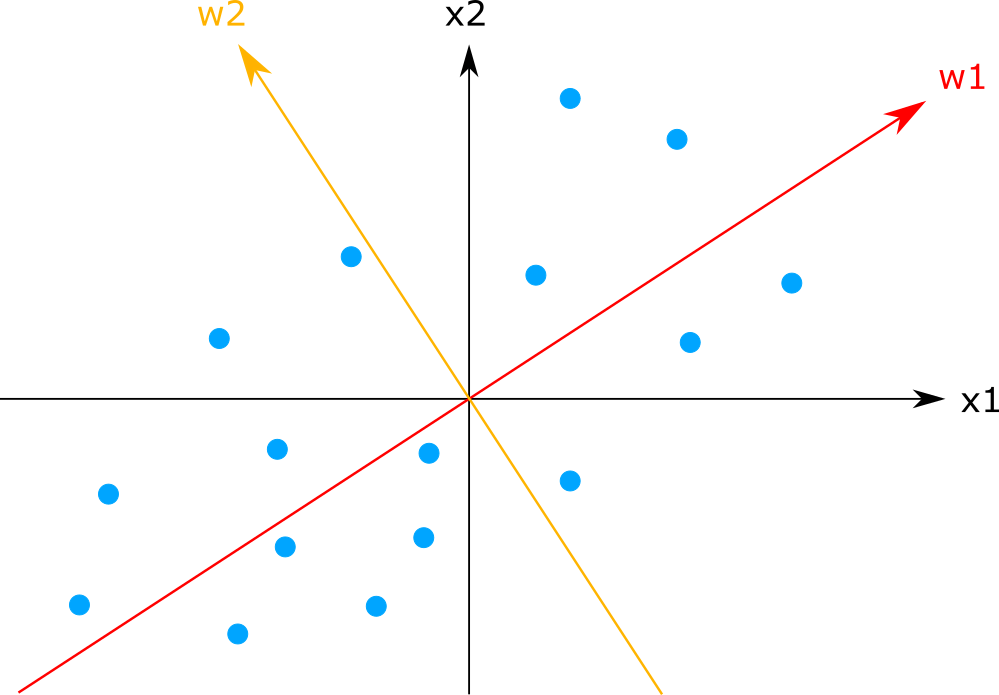
主成分分析はデータの次元を減らしてデータを近似したり、データ分析に使われたりします。音のアレイ信号処理では、音源の位置を推定する音源定位に使われたりします。
主成分の求め方
以下の空間相関行列\(\ \boldsymbol{R}\ \) の固有ベクトルが主成分の方向となります。
$$
\boldsymbol{R}=E[\boldsymbol{x[n]x^H[n]}]
$$
\(\ E[\cdot]\ \)は期待値演算、\(\boldsymbol{x}[n]=[x_1[n], \cdots, x_m[n], \cdots, x_M[n]]^T\)、\( \{\cdot\}^H\) はエルミート転置です。
固有値 \(\lambda_i\)、固有ベクトル \( \boldsymbol{w_i}\) は次式を満たすものとなっており、M個(マイクの個数)あります。
$$
\boldsymbol{R w_i} = \lambda_i \boldsymbol{w_i}
$$
相関行列の最大の固有値が第1主成分の分散となり、最大の固有値に対応する固有ベクトルが第1主成分の方向となります。
それから、2番目に大きい固有値が第2主成分の分散になり、その固有値に対応する固有ベクトルが第2主成分の方向、3番目に大きい固有値が第3主成分の分散になり、その固有値に対応する・・・となっていきます。
期待値演算については、複数の信号の平均(集合平均)を求める演算ですが、普通は1回分の観測信号しか得られないことがほとんどのため、以下のエルゴード性を仮定して解析を行います。
$$
E[\boldsymbol{x[n]x^H[n]}] = \frac{1}{N} \sum_{n=0}^{N-1}\boldsymbol{x[n]x^H[n]}
$$
\( N\) はサンプル数です。
つまり、集合平均と時間平均が同じになると仮定して計算を行います。
主成分の求め方の詳細
相関行列の固有ベクトルが主成分の方向となることはいろいろな文献で紹介されていますが、なぜ固有ベクトルが主成分の方向となるかの説明はあまりないと思います。今回、文献をいろいろ探して、参考文献 [1] にその説明がありましたので紹介します。
観測値を\( \boldsymbol{x}\) (複素ベクトル)とすると、単位ベクトル \( \boldsymbol{w_1}\) 上に射影された \( \boldsymbol{x}\) の成分である\(y_1\) は以下のようになります。
$$
\begin{align}
y_1 &= \frac{\boldsymbol{w_1^H x}}{\boldsymbol{w_1^H w_1}} \\[5pt]
&= \boldsymbol{w_1^H x}
\end{align}
$$
\( E[\boldsymbol{x}]=\boldsymbol{0}\) であるとすると、\( y_1\) の分散は以下のように計算されます。
$$
\begin{align}
E[|y_1|^2] - (E[y])^2 &= E[y_1y_1^*] - 0 \\[5pt]
&= \boldsymbol{w_1^H} E[\boldsymbol{xx^H}] \boldsymbol{w_1} \\[5pt]
&= \boldsymbol{w_1^H R w_1}
\end{align}
$$
\( ||\boldsymbol{w_1}||=1\) (単位ベクトル)という拘束条件を満たしながら、\(y_1\) の分散(平均パワー)が最大となるように \(\boldsymbol{w_1}\) を決定します。
この問題はラグランジュの未定乗数法によって、次式を最大化する問題に置き換えられます。
$$
J = \boldsymbol{w_1^H R w_1} + \lambda (1-\boldsymbol{w_1^H w_1})
$$
\(\boldsymbol{w_1^*}\) で偏微分して、\( \boldsymbol{0}\) とおくことにより次式のようになります。
$$
\begin{align}
\frac{\partial J}{\partial \boldsymbol{w_1^*}} &= \boldsymbol{0} \\[5pt]
\boldsymbol{R w_1} - \lambda \boldsymbol{w_1} &= \boldsymbol{0} \\[5pt]
\boldsymbol{R w_1} &= \lambda \boldsymbol{w_1}
\end{align}
$$
ここでは、以下の複素ベクトルの偏微分の公式を用いています。
$$
\begin{align}
\frac{\partial}{\partial \boldsymbol{w^*}} \boldsymbol{w^H R w} &= \boldsymbol{R w} \\[5pt]
\frac{\partial}{\partial \boldsymbol{w^*}} \boldsymbol{w^H w} &= \boldsymbol{w}
\end{align}
$$
つまり、\(\boldsymbol{R w_1} = \lambda \boldsymbol{w_1}\) は固有値問題となるので、相関行列の固有ベクトルが主成分の方向となります。
また、さきほどの式に左から\( \boldsymbol{w_1}^H\) をかけることで、
$$
\boldsymbol{w_1^H R w_1} = \lambda
$$
左辺が \( y_1\) の分散となるので、主成分の分散は相関行列の固有値となります。
さらに、固有ベクトルは複数ありますが、第1主成分は分散が最大となるように決定しますので、最大の固有値に対応する固有ベクトルが第1主成分の方向となります。
第2主成分、第3主成分については、これまでに求めた主成分に直交するという条件の下で、\(J\) が最大となるように決定します。固有ベクトルは直交するので、2番目、3番目に大きい固有値に対応した固有ベクトルが第2主成分、第3主成分となります。
部分空間法
部分空間法というのは、参考文献 [1] から引用すると以下のようなことです。
部分空間法は、観測信号を空間相関行列の固有ベクトルが張る固有空間に変換し、解析・処理する方法である。
つまり、主成分分析で得られたものを使った解析や処理のことです。
マイクの数が音源の数より多いときは、信号を低次の部分空間で表すことができます。
さらに、部分空間法を利用するMUSIC法などは精度の良い音源定位を実現できます。
ここでは、信号を低次の部分空間で表せることを説明します。
観測信号を短時間フーリエ変換したとき、それは以下のように表せます。
$$
\boldsymbol{X}[i,k] = \boldsymbol{A}[k] \boldsymbol{S}[i,k] \hspace{3em} (A)
$$
ここで、
$$
\boldsymbol{X}[i,k]=[X_1[i,k] \cdots X_m[i,k] \cdots X_M[i,k]]^T
$$
は観測信号を短時間フーリエ変換したもの、
$$
\boldsymbol{S}[i,k]=[S_1[i,k] \cdots S_j[i,k] \cdots S_J[i,k]]^T
$$
は音源信号を短時間フーリエ変換したもの、\( i\) はフレーム番号、\(k\) は周波数ビン番号です。\(\boldsymbol{A}[k]\) はアレイマニフォールド行列で以下のように表せます。
\boldsymbol{A}[k] =
\begin{bmatrix}
A_{11}[k] & \cdots & A_{1j}[k] & \cdots & A_{1J}[k] \\
\vdots & \ddots & & & \vdots \\
A_{m1}[k] & & A_{mj}[k] & & A_{mJ}[k] \\
\vdots & & & \ddots & \vdots \\
A_{M1}[k] & \cdots & A_{Mj}[k] & \cdots & A_{MJ}[k] \end{bmatrix}
$$
アレイマニフォールド行列の要素は、各音源から各センサまでの経路の伝達関数となっています。
ビームフォーミングで特定方向の音源を強調 では音源が1つでしたので、アレイマニフォールドベクトルでしたが、今回は音源が複数ある場合を考えるので、アレイマニフォールド行列となっています。
音源の数を\( J=2\)、マイクの数を\(M=3\) とします。このとき、観測信号は以下のように表せます。
$$
\begin{bmatrix}
X_{1} \\
X_{2} \\
X_{3}
\end{bmatrix}=
\begin{bmatrix}
A_{11} & A_{12} \\
A_{21} & A_{22} \\
A_{31}& A_{32}
\end{bmatrix}
\begin{bmatrix}
S_{1} \\
S_{2} \\
\end{bmatrix}
$$
この式を整理して、\( S_1, S_2\) を消去すると、以下のような式となります。
$$
(A_{31}A_{22}-A_{21}A_{32})X_{1}+(A_{11}A_{32}-A_{31}A_{12})X_{2}+(A_{21}A_{12}-A_{11}A_{22})X_{3} = 0
$$
これは平面の式になりますので、観測信号は3次元空間において平面上に存在します。したがって、主成分分析で第2主成分の方向まで求めれば、それを使って観測信号を2次元(音源の数の次元)で表現できるということです。
また、アレイマニフォールド行列の列ベクトルであるアレイマニフォールドベクトル\( \boldsymbol{A_1, A_2}\)と固有ベクトルの幾何学的関係は図のようになります。
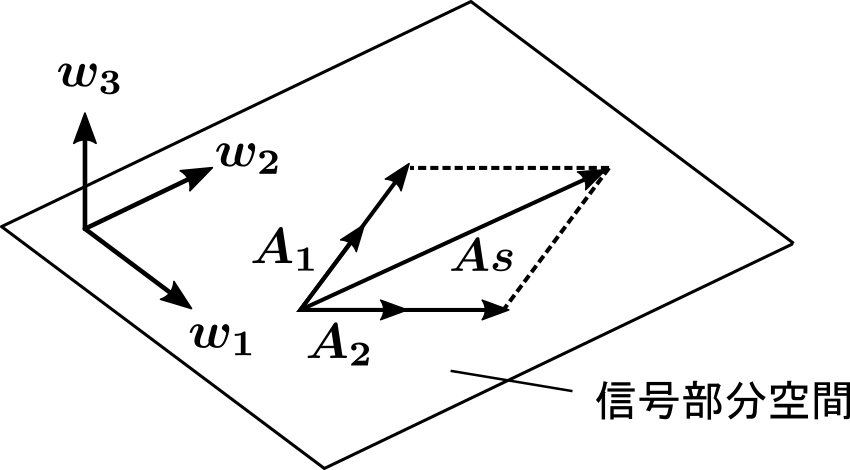
アレイマニフォールドベクトルによって張られる空間は信号部分空間と呼びます。固有ベクトル\( \boldsymbol{w_1, w_2}\ \)については信号部分空間の正規直交基底となっています。
プログラム
各周波数ビンで主成分分析を行うプログラムが以下です。
import soundfile as sf
import numpy as np
import scipy.signal as sg
import matplotlib.pyplot as plt
# パラメータ
dir_name = "mic/" # 録音データがあるディレクトリ
png_name = "eigen.png" # 出力するグラフのファイル名
n_mic = 8 # マイクの数
N = 512 # 窓の大きさ
window = "hann" # 窓の種類
f_l = 800 # 固有値を合計する周波数の下限
f_h = 3000 # 固有値を合計する周波数の上限
# WAVファイル名のリスト作成
wav_list = []
for i in range(n_mic):
wav_list.append("mic"+str(i)+".wav")
# WAVファイルを読み込む
for i, wav_name in enumerate(wav_list):
x, fs = sf.read(dir_name+wav_name)
if i==0:
audio=np.zeros((n_mic,len(x)))
audio[0,:] = x
else:
audio[i,:] = x
# 周波数ビンを求める
k_l = int(f_l/(fs/N))
k_h = int(f_h/(fs/N))
# 短時間フーリエ変換(STFT)を行う X.shape=(n_mic, n_bin, n_frame)
f, t, X = sg.stft(audio, fs, window=window, nperseg=N)
n_bin = X.shape[1]
# 空間相関行列を求める
XH = np.conjugate(X)
XXH = np.einsum("mki,nki->mnki", X, XH)
R = np.mean(XXH, axis=3)
# 固有値を求めて昇順に並べる
eig_val = np.zeros((n_mic, n_bin), dtype=np.complex64)
eig_vec = np.zeros((n_mic, n_mic, n_bin), dtype=np.complex64)
for k in range(n_bin):
# 固有値と固有ベクトルを求める
eig_val_k, eig_vec_k = np.linalg.eig(R[:,:,k])
# 固有値の大きい順に固有値と固有ベクトルを並べる
sort = np.argsort(np.abs(eig_val_k))[::-1]
eig_val[:,k] = eig_val_k[sort]
eig_vec[:,:,k] = eig_vec_k[:,sort]
# 固有値の絶対値の合計を求める
eig_sum = np.sum(np.abs(eig_val[:,k_l:k_h]), axis=1)
eig_val_a = eig_sum/eig_sum[0] #一番目の固有値の合計で正規化
i = np.arange(1,n_mic+1)
# グラフを出力
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(i, 20*np.log10(eig_val_a), c="red", marker='o')
ax.set_xlabel("Eigenvalue number")
ax.set_ylabel("Eigenvalue [dB]")
fig.savefig(png_name)
# ターミナルに出力
print(20*np.log10(eig_val_a))
このプログラムで 800Hzから3000Hz の固有値の絶対値の合計を以下のように求めています。
$$
\Lambda_i = \sum_{k=k_l}^{k_h-1} |\lambda_i[k]|
$$
\(k_l\) は800Hzに対応する周波数ビン番号、\(k_h\) は3000Hz に対応する周波数ビン番号です。
実験
信号を低次の部分空間で表せることを実験で確認します。
方法
室内音響シミュレーションにはPythonのライブラリであるPyRoomAcousticsを用いました。
シミュレーション上で図のように音源とマイクを配置して、8個のマイクで音楽データを録音しました。
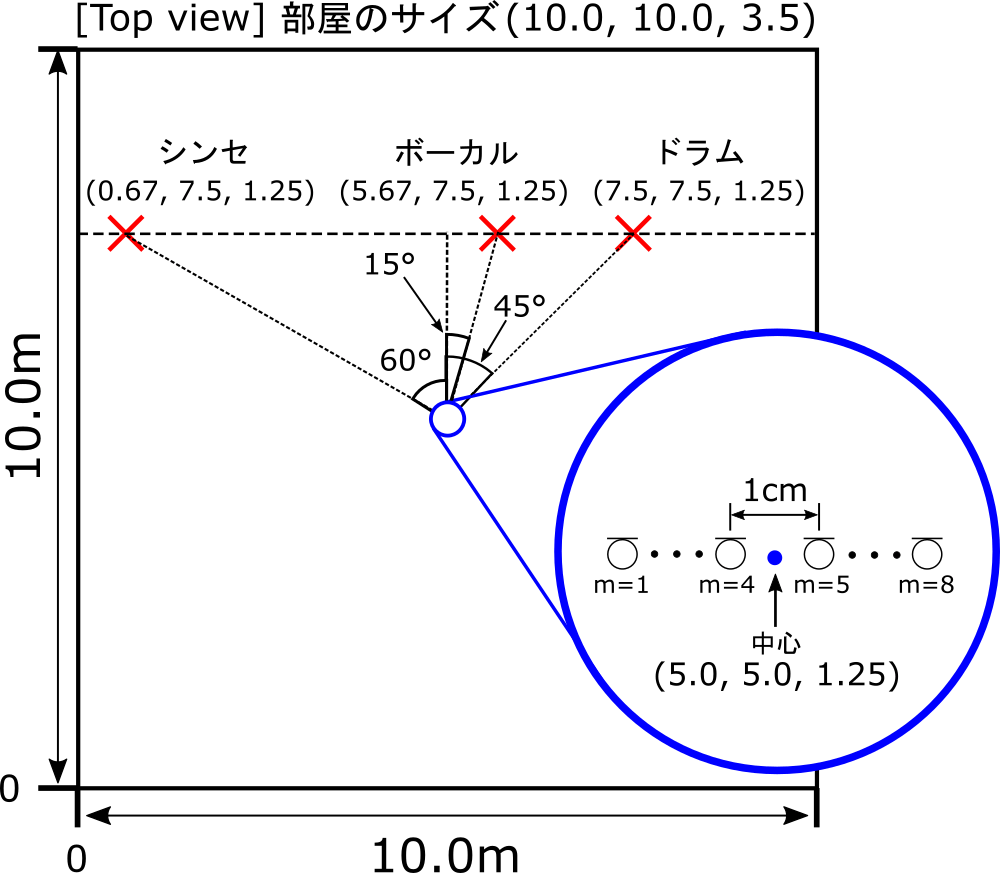
残響時間は0.2秒、収録時のサンプリング周波数は16kHz 、SN比は90dB(ほとんど雑音なし)に設定しました。また、反射・残響あり、反射・残響なしの2つの場合について調べました。
以下をクリックすると、シミュレーションに用いた Python のコード room_sim.py が展開されます。
room_sim.py (クリックで展開)
import numpy as np
import pyroomacoustics as pra
import soundfile as sf
from librosa import resample
fs = 16000 # リサンプリング後の周波数
rt60_tgt = 0.2 # 残響時間
room_size = [10, 10, 3.5] # 部屋の大きさ
SNR = 90 # SN比
dir_src = "src/" # 音源のフォルダ
dir_mic = "mic2/" # 録音したデータのフォルダ
src_list = ["Synth.wav", "Vox.wav", "drum.wav"]
# 音源とマイクの位置を決定
center = [5.0,5.0] # 中心の位置
n_src = 3 # 音源の数
n_mic = 8 # マイクの数
d = 0.01 # マイクの間隔 [m]
# 音源を配置
s_locs = np.zeros((2,3))
s_locs[0,:] = [0.67, 5.67, 7.5] # 90度 15度 45度
s_locs[1,:] = [7.5, 7.5, 7.5]
s_locs = np.insert(s_locs, 2, 1.25, axis=0)
print(s_locs) # 音源の位置を表示
for i in range(n_src):
print(np.degrees(np.arctan2(s_locs[1,i]-5, s_locs[0,i]-5))-90)
# マイクを線状アレイで配置
m_locs = pra.linear_2D_array(center, n_mic, 0, d)
m_locs = np.insert(m_locs, 2, 1.25, axis=0)
# WAVファイルを読み込む
audio = []
for i, src_name in enumerate(src_list):
x, fs_tmp = sf.read(dir_src+src_name)
x = resample(x, fs_tmp, fs)
audio.append(x)
audio = np.array(audio)
# 残響時間と部屋の大きさから吸音率と反射回数を決定
e_absorption, max_order = pra.inverse_sabine(rt60_tgt, room_size)
# 部屋の反射・残響なしの場合
#e_absorption = 1.0
#max_order=0
# 部屋の作成
room = pra.ShoeBox(
room_size, fs=fs, materials=pra.Material(e_absorption), max_order=max_order
)
# 部屋に音源を配置
for i in range(n_src):
room.add_source(s_locs[:,i], signal=audio[i,:], delay=0)
# 部屋にマイクを配置
room.add_microphone_array(
pra.MicrophoneArray(m_locs, fs=fs)
)
# シミュレーションする
room.simulate(snr=SNR)
# マイクで録音した音を書き出す
mic_data = room.mic_array.signals
mic_data = mic_data/np.max(np.abs(mic_data)) # ノーマライズ
for i in range(n_mic):
name = dir_mic+"mic"+str(i)+".wav"
sf.write(name, mic_data[i,:], fs, subtype='PCM_16')信号を低次元(音源の数の次元)で表せる場合、1~3番目の固有値は大きくなり、4番目以降の固有値は急激に小さくなるはずです。
結果
番号ごとの固有値の合計は以下のようになりました。
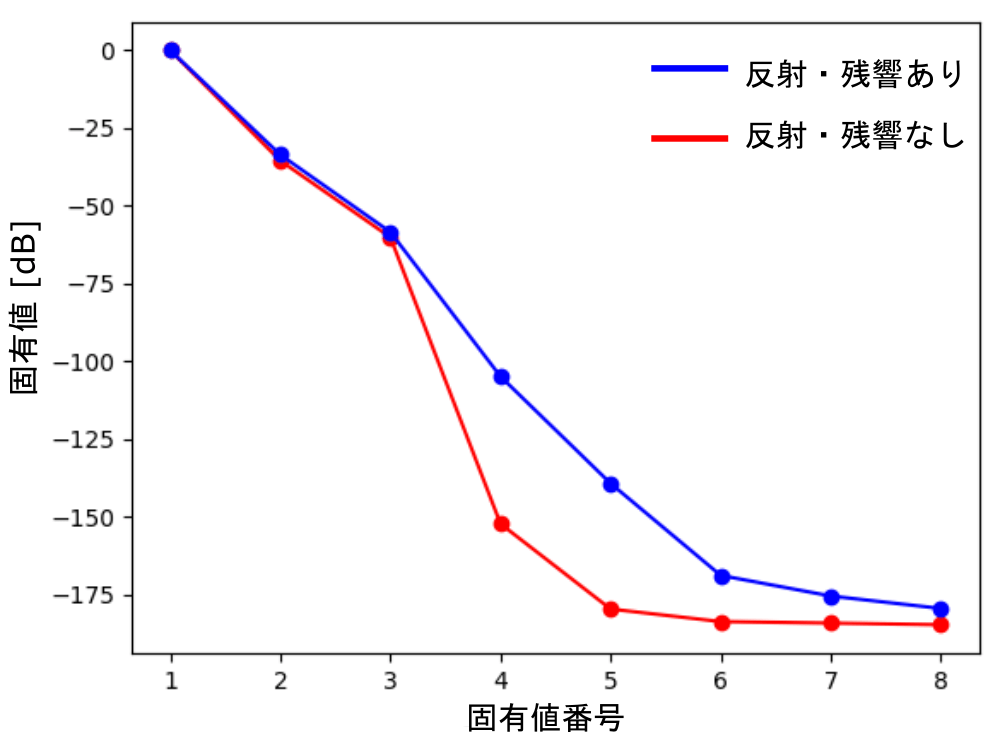
反射・残響なしの場合は予想したように、4番目の固有値から急激に小さくなっています。しかし、反射・残響ありの場合は、急激に小さくなってはいません。
これは、反射・残響ありの場合、観測信号が式 (A) のように表せないからです。残響時間が長い場合、前のフレームの音源信号\( \boldsymbol{S}[i-1,k]\) によっても観測信号は影響されるので、低次元で表せなくなるということです。
おわりに
本記事では主成分分析を紹介しました。次回は、主成分分析を利用した音源定位であるMUSIC法について紹介しようと思います。
参考文献
[1] 浅野太、”音のアレイ信号処理 音源の定位・追跡と分離”、コロナ社、2011.
