本記事ではMUSIC(MUltiple SIgnal Classification)法をPythonで実装しました。MUSIC法はSchmidtにより1986年に提案されており、音源の位置を推定する技術(音源定位)では最も代表的な手法ではないかと思います。今回は、シミュレーション環境で録音した音を用いて、MUSIC法の有効性を確かめました。
本記事は前回の記事(音声・音響処理で使う主成分分析)を読んでいることを前提に書かれています。
MUSIC法
まず、MUSIC法を理解するのに必要な部分空間の直交性について説明します。それから、狭帯域の信号と広帯域の信号に対するMUSIC法について説明したいと思います。
部分空間の直交性
前回の記事(音声・音響処理で使う主成分分析)でも説明したように、アレイマニフォールドベクトルによって張られる空間は信号部分空間と呼び、空間相関行列の固有ベクトル\(\ \boldsymbol{w_1, w_2}\ \) については信号部分空間の正規直交基底となっています。
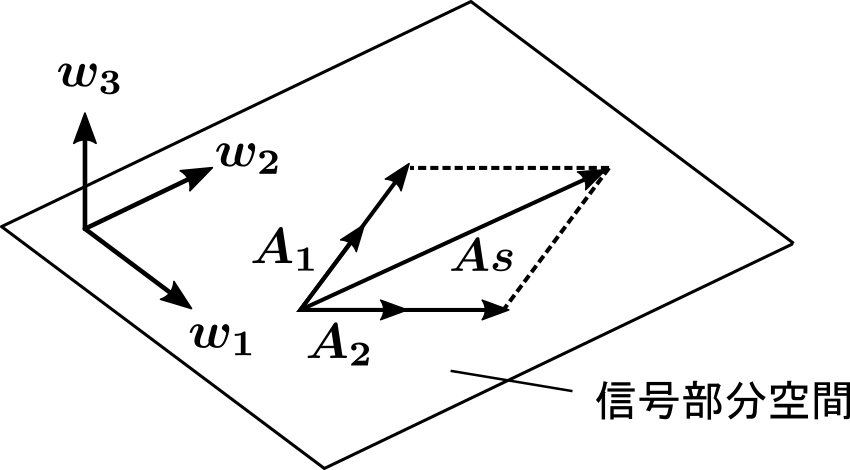
一方、音源の数より大きい番号の固有ベクトル \(\boldsymbol{w}_3\) については以下の式が成り立ちます。
$$
\boldsymbol{A}^H \boldsymbol{w}_3 = \boldsymbol{0}
$$
音源の数を\( J\) 、マイクの数を\( M\)とすると、一般的には以下の式が成り立ちます。
$$
\boldsymbol{A}^H \boldsymbol{w}_i = \boldsymbol{0} \hspace{1em} (i=J+1, \cdots, M)
$$
\(\boldsymbol{A}=[\boldsymbol{A}_1, \cdots, \boldsymbol{A}_J]\), \(\boldsymbol{A}_j=[A_{1j}, \cdots, A_{Mj} ]^T\) とすると、
$$
\begin{align}
\boldsymbol{A}_j^H \boldsymbol{w}_i = \boldsymbol{0} \hspace{1em} &(i=J+1, \cdots, M) \\
&(j=1,\cdots,J)
\end{align}
$$
つまり、アレイマニフォールドベクトルと音源の数より大きい番号の固有ベクトルは直交するという性質があります。
空間スペクトル
MUSIC法では次式の空間スペクトル\(P_k(\theta)\)(\( \theta\ \) 方向から到来する信号のパワー)によって音源の到来方向を求めます。
$$
\begin{align}
P_{k}(\theta) = \frac{||\boldsymbol{a}_k(\theta)||^2}{\sum_{i=J+1}^{M}|\boldsymbol{a}_k^H(\theta)\boldsymbol{w}_i|^2} \\[5pt]
= \frac{\boldsymbol{a}_k^H(\theta)\boldsymbol{a}_k(\theta)}{\boldsymbol{a}_k^H(\theta)\boldsymbol{W}\boldsymbol{W}^H \boldsymbol{a}_k(\theta)}
\end{align}
$$
ここで、
$$
\begin{equation}
\boldsymbol{a}_k(\theta)
=
\begin{bmatrix}
\exp{\left(-j 2\pi \frac{k}{N}f_s \tau_1(\theta)\right)} \\
\vdots \\
\exp{\left(-j 2\pi \frac{k}{N}f_s \tau_M(\theta)\right)}
\end{bmatrix}
\end{equation}
$$
\(\boldsymbol{a}_k(\theta)\)は周波数ビン番号 k、\(\theta\) 方向の仮のアレイマニフォールドベクトルで、線状アレイの場合、遅延時間は以下のようになります。
$$
\begin{equation}
\tau_m(\theta)=\left((m-1)-\frac{M-1}{2}\right) \frac{d_x}{c} \sin{\theta}
\end{equation}
$$
\( d_x\) はマイクの間隔、\( c\) は音速です。遅延時間の求め方を知りたい方はビームフォーミングで特定方向の音源を強調という記事をご覧ください。
また、
$$
\boldsymbol{W}=[\boldsymbol{w}_{J+1}, \cdots, \boldsymbol{w}_{M}]
$$
です。
\( \theta = 0°\sim 180°\) の空間スペクトルを計算して、空間スペクトルのピークの位置が音源の到来方向となります。ピークが音源の数よりも多くある場合は、空間スペクトルが大きいピークの位置を音源の到来方向とします。
なぜMUSIC法ではこのような空間スペクトルを使うかというと、部分空間の直交性から、\( \boldsymbol{a}_k(\theta)\) が正しいアレイマニフォールドベクトルの場合、分母は 0 となり、空間スペクトルはピークを持つからです。
分子の\( ||\boldsymbol{a}(\theta)||^2\) はアレイマニフォールドベクトルの正規化のための項です。あってもなくてもピークの位置は変わらないため、計算しなくてもいいです。
広帯域信号の場合
さきほどの方法は狭帯域信号に対する方法でした。音楽信号などの広帯域信号の場合、周波数ビンごとの情報を統合して、最終的な推定結果を得る必要があります。
周波数ビンごとの情報を統合する手法はいくつかあるようですが、この記事では空間スペクトルを平均します。
周波数ビンごとの空間スペクトルを次式のように重み付き平均して、最終的な空間スペクトルを推定します。
$$
\bar{P}(\theta) = \frac{1}{K} \sum_{k=k_l}^{k_h} \beta_k P_k(\theta)
$$
$$
\beta_k = \left[\sum_{i=1}^J \lambda_i[k] \right]^\alpha
$$
ここで、\(K\) は周波数ビンの数、\( \lambda_i\) は空間相関行列の固有値、\(\alpha\) は定数で、\(\alpha=1\) や \(\alpha=1/2\) とします。
空間相関行列の固有値は信号の平均パワーに相当しますので、パワーが大きい周波数ビンほど重みづけするということです
プログラム
MUSIC法によって空間スペクトルと音源の方向を求めるプログラムは以下です。
import soundfile as sf
import numpy as np
import scipy.signal as sg
import matplotlib.pyplot as plt
# パラメータ
dir_name = "mic/" # 録音データがあるディレクトリ
png_name = "music.png" # 出力するグラフの画像名
n_mic = 8 # マイクの数
n_src = 3 # 音源の数
N = 512 # 窓の大きさ
window = "hann" # 窓の種類
d = 0.01 # マイクの間隔[m]
c = 340 # 音速[m/s]
freq_l = 800 # 空間スペクトルを計算する周波数の下限
freq_h = 3000 # 空間スペクトルを計算する周波数の下限
# WAVファイル名のリスト作成
wav_list = []
for i in range(n_mic):
wav_list.append("mic"+str(i)+".wav")
# WAVファイルを読み込む
for i, wav_name in enumerate(wav_list):
x, fs = sf.read(dir_name+wav_name)
if i==0:
audio=np.zeros((n_mic,len(x)))
audio[0,:] = x
else:
audio[i,:] = x
# 周波数ビンに変換
k_l = int(freq_l/(fs/N))
k_h = int(freq_h/(fs/N))
# 短時間フーリエ変換(STFT)を行う X.shape=(n_mic, n_bin, n_frame)
f, t, X = sg.stft(audio, fs, window=window, nperseg=N)
n_bin = X.shape[1]
# 空間相関行列を求める
XH = np.conjugate(X)
XXH = np.einsum("mki,nki->mnki", X, XH)
R = np.mean(XXH, axis=3)
# 固有値を求めて大きい順に並べる
eig_val = np.zeros((n_mic, n_bin), dtype=np.complex64)
eig_vec = np.zeros((n_mic, n_mic, n_bin), dtype=np.complex64)
beta = np.zeros(n_bin)
for k in range(n_bin):
eig_val_k, eig_vec_k = np.linalg.eig(R[:,:,k]) # 固有値、固有ベクトルを求める
sort = np.argsort(-1.0*np.abs(eig_val_k)) # 大きい順にargsort
eig_val[:,k] = eig_val_k[sort] # 固有値を大きい順に並べる
eig_vec[:,:,k] = eig_vec_k[:,sort] # 固有ベクトルも並べ替える
W = eig_vec[:,n_src:,:] # 音源の数より大きい番号の固有ベクトル
beta = np.sum(np.abs(eig_val[:n_src,:]), axis=0) # 重みβを求める
# 空間スペクトル作成
theta = np.linspace(-90.0, 90.0, 181)
P_MU = np.zeros_like(theta)
a = np.zeros((n_mic, 1, n_bin), dtype=np.complex64)
for i, th in enumerate(theta):
th = np.radians(th) # deg -> rad 変換
# 直線状アレイのアレイ・マニフォールド・ベクトルの作成
for k in range(n_bin):
fk = fs*k/N # 周波数
for m in range(n_mic):
delay = (m-(n_mic-1)/2)*d*np.sin(th)/c # 遅延時間
a[m,0,k] = np.exp(-1j*2*np.pi*fk*delay)
aH = np.conjugate(a)
aHa = np.einsum("mik,mjk->ijk", aH, a)
P_MU_th = np.einsum("mik,mek->iek", aH, W)
P_MU_th = np.einsum("iek,jek->ijk", P_MU_th, np.conjugate(P_MU_th))
P_MU_th = np.abs(aHa)/np.abs(P_MU_th)
P_MU[i] = np.mean(beta[k_l:k_h+1]*P_MU_th[0,0,k_l:k_h+1])
# グラフを出力
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(theta, 10*np.log10(P_MU), c="red")
ax.set_xlim([-90,90])
ax.set_xlabel("Direction [deg]")
ax.set_ylabel("Spatial spectrum [dB]")
fig.savefig(png_name)
# 候補を出力
index=sg.argrelmax(P_MU) # ピークのあるインデックスを求める
sort=np.argsort(-1.0*P_MU[index]) # ピークの中でargsort
for i in range(n_src):
print(theta[index[0][sort[i]]]) # 大きい順に方向を表示
18~30行目:指定したディレクトリの中にあるmicX.wavという名前のWAVファイルをマイクの数だけ読み込む。
32~34行目:空間スペクトルを平均する周波数の下限と上限を周波数ビン番号に変換する。
40~43行目:周波数ビンごとに空間相関行列を求める。
45~53行目:固有値を大きい順に並べかえ、対応する固有ベクトルも同じように並べかえる。
55~56行目:\(\boldsymbol{W}, \beta_k\) を求める。
58~75行目:\( -90^\circ \leq \theta \leq 90^\circ\) の空間スペクトル\(P_k\) を求める。
86~90行目:空間スペクトルのピークの位置を到来方向の候補としてターミナルに出力する。
シミュレーション実験
室内音響シミュレーションで作成した音に対してMUSIC法を使用して、音源の方向を推定しました。
方法
シミュレーション環境の録音方法は前回の記事:音声・音響処理で使う主成分分析での方法と同様です。
室内音響シミュレーションにはPythonのライブラリであるPyRoomAcousticsを用いました。
シミュレーション上で図のように音源とマイクを配置して、8個のマイクで音楽データを録音しました。
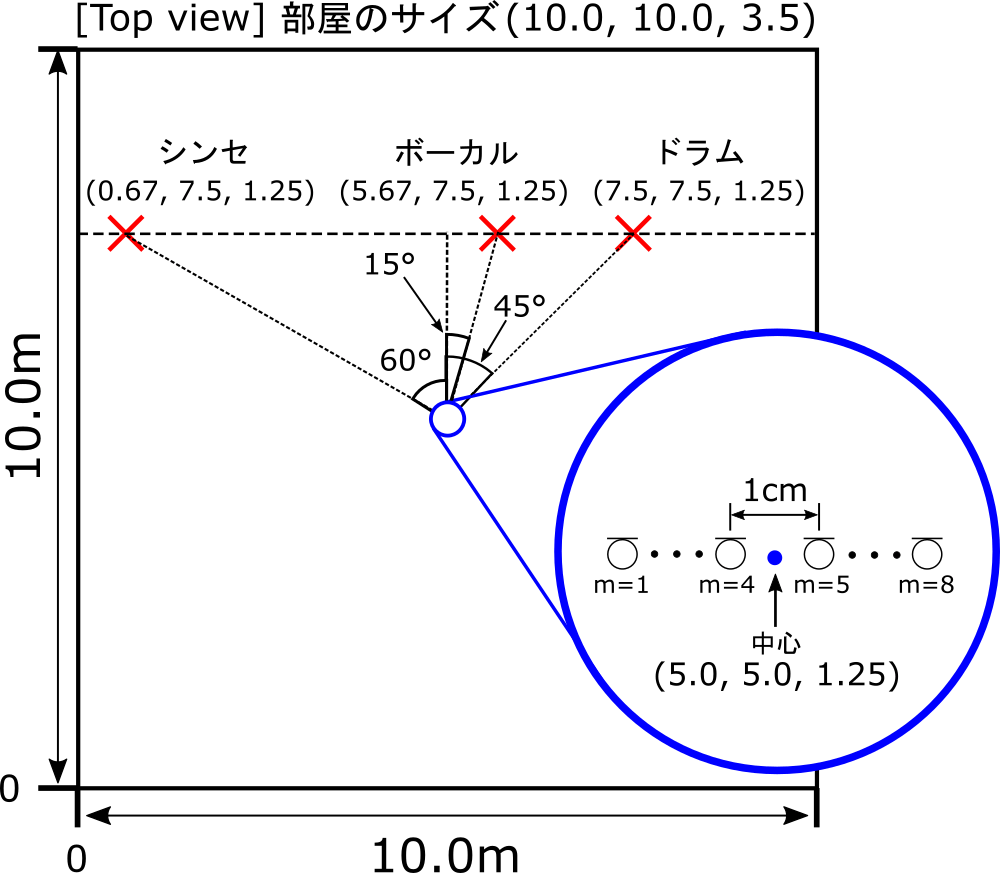
残響時間は0.2秒、収録時のサンプリング周波数は16kHz 、SN比は90dB(ほとんど雑音なし)に設定しました。
以下をクリックすると、シミュレーションに用いたPython のコード room_sim.py が展開されます。
room_sim.py(クリックで展開)
import numpy as np
import pyroomacoustics as pra
import soundfile as sf
from librosa import resample
fs = 16000 # リサンプリング後の周波数
rt60_tgt = 0.2 # 残響時間
room_size = [10, 10, 3.5] # 部屋の大きさ
SNR = 90 # SN比
dir_src = "src/" # 音源のフォルダ
dir_mic = "mic/" # 録音したデータのフォルダ
src_list = ["Synth.wav", "Vox.wav", "drum.wav"]
# 音源とマイクの位置を決定
center = [5.0,5.0] # 中心の位置
n_src = 3 # 音源の数
n_mic = 8 # マイクの数
d = 0.01 # マイクの間隔 [m]
# 音源を配置
s_locs = np.random.rand(2,3) # 0以上1未満の2 x 3の配列
#s_locs[0,:] = s_locs[0,:] * 10 # 1行目0以上10未満にする
#s_locs[1,:] = (s_locs[1,:] * 3) + 7.0 # 2行目5以上10未満にする
s_locs[0,:] = [3.56, 5.67, 6.44]
s_locs[1,:] = [7.5, 7.5, 7.5]
s_locs = np.insert(s_locs, 2, 1.25, axis=0)
print(s_locs) # 音源の位置を表示
for i in range(n_src):
print(np.degrees(np.arctan2(s_locs[1,i]-5, s_locs[0,i]-5))-90)
# マイクを線状アレイで配置
m_locs = pra.linear_2D_array(center, n_mic, 0, d)
m_locs = np.insert(m_locs, 2, 1.25, axis=0)
# WAVファイルを読み込む
audio = []
for i, src_name in enumerate(src_list):
x, fs_tmp = sf.read(dir_src+src_name)
x = resample(x, fs_tmp, fs)
audio.append(x)
audio = np.array(audio)
# 残響時間と部屋の大きさから吸音率と反射回数を決定
e_absorption, max_order = pra.inverse_sabine(rt60_tgt, room_size)
# 部屋の作成
room = pra.ShoeBox(
room_size, fs=fs, materials=pra.Material(e_absorption), max_order=max_order
)
# 部屋に音源を配置
for i in range(n_src):
room.add_source(s_locs[:,i], signal=audio[i,:], delay=0)
# 部屋にマイクを配置
room.add_microphone_array(
pra.MicrophoneArray(m_locs, fs=fs)
)
# 部屋をプロットする
fig, ax = room.plot()
ax.set_zlim(0,room_size[2])
fig.savefig("room.png")
# シミュレーションする
room.simulate(snr=SNR)
# マイクで録音した音を書き出す
mic_data = room.mic_array.signals
mic_data = mic_data/np.max(np.abs(mic_data)) # ノーマライズ
for i in range(n_mic):
name = dir_mic+"mic"+str(i)+".wav"
sf.write(name, mic_data[i,:], fs, subtype='PCM_16')結果
プログラムmusic.pyで処理した結果は図のようになりました。
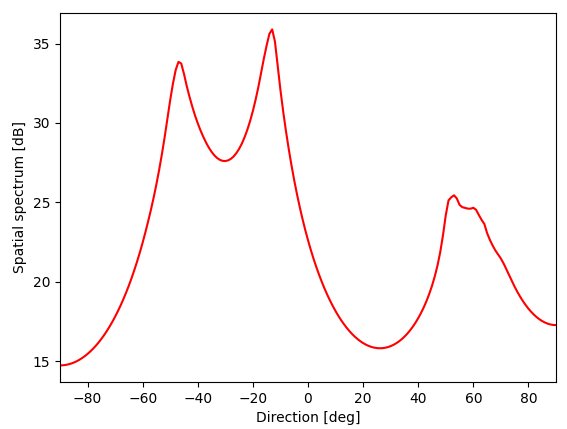
また、ターミナルに出力された到来方向の推定結果は表のようになりました。
| 音源 | 推定 | 正解 |
|---|---|---|
| シンセ | \(53.0\) 度 | \(60.0\) 度 |
| ボーカル | \(-13.0\) 度 | \(-15.0\) 度 |
| ドラム | \(-47.0\) 度 | \(-45.0\) 度 |
シンセの方向については7度ずれていましたが、だいたい推定できていました。
補足:シンセの方向を30度、ボーカルの方向を-15度、ドラムの方向を-30度としたとき、図4のような結果となりました。
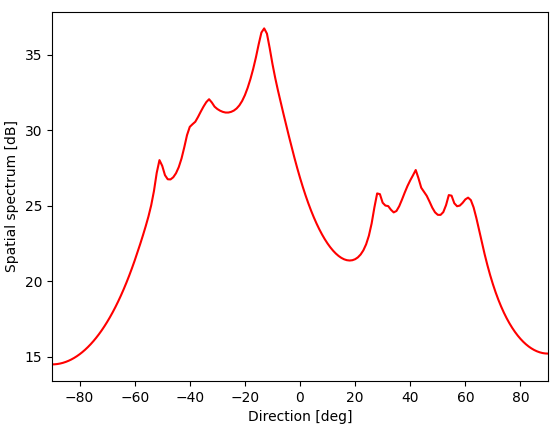
また、ターミナルに出力された到来方向の推定結果は以下の表のようになりました。
| 音源 | 推定 | 正解 |
|---|---|---|
| シンセ | \(-51.0\) 度 | \(30.0\) 度 |
| ボーカル | \(-13.0\) 度 | \(-15.0\) 度 |
| ドラム | \(-33.0\) 度 | \(-30.0\) 度 |
音源どうしが近すぎるためか、空間スペクトルにいくつもピークが生じてしまい、シンセの方向については推定できませんでした。一応、30度付近にピークはありますが、他のピークのほうが大きいため、推定結果がずれてしまいました。
原因としては、反射・残響により部分空間の直交性が成り立たなくなったことでビーム幅が広がり、近すぎる音源どうしを分離できなかったのではないかと思っています。
おわりに
本記事ではMUSIC法をPythonで実装して、MUSIC法の有効性を確認しました。他の音源定位の手法も実装できたら、手法間で音源定位の精度を比較しようかなと思います。
参考文献
[1] 浅野太、”音のアレイ信号処理 音源の定位・追跡と分離”、コロナ社、2011.
■変更履歴
・2025/01/30:タグの削除
