ねっちゅう工房

オールパスフィルターによるリバーブの実装

本記事では、オールパスフィルタによるリバーブを実装してみました。オールパスフィルタとは振幅特性を変えずに位相特性を変えるフィルタのことです。

くし型フィルタによるリバーブの実装を以前紹介しましたが、シュレーダーの論文 [1] ではくし型フィルタの欠点をいくつか指摘しており、その欠点を改善する方法としてオールパスフィルタによるリバーブを提案しています。

この記事では、文献 [1] で記載されていた「くし型フィルタの欠点」と「オールパスフィルタによるリバーブ」について紹介していきます。

目次

くし型フィルタの欠点

文献 [1] ではくし型フィルタの欠点を以下の２つ指摘しています。

  • フィルタの振幅特性が平坦ではない
  • エコー密度が小さい

エコー密度とは、1つのパルスが入力されたときのリバーブエフェクタが出力する1秒あたりの反射音の数です。

リバーブの振幅特性が平坦ではない

くし型フィルタである以下の式

$$
y[n] = x[n] + g y[n-D] $$

は下図のようにくし型の振幅特性をしています。

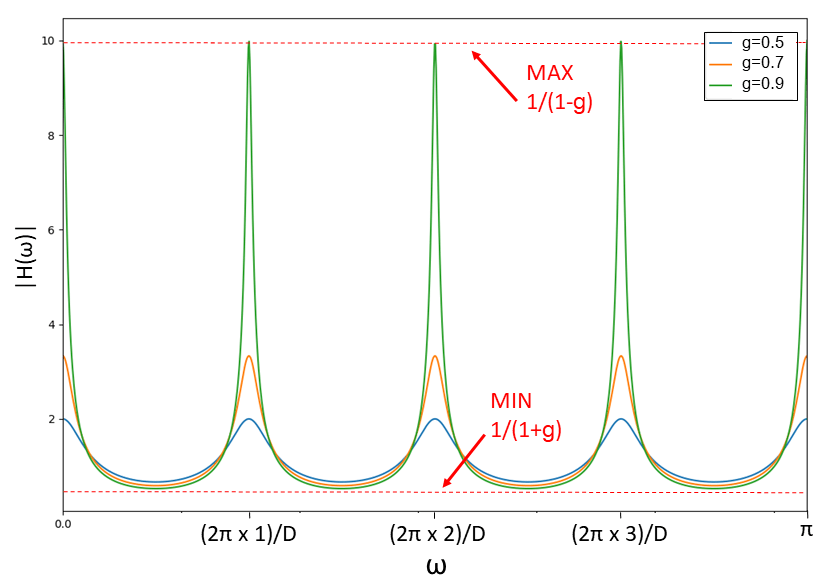
図：くし型フィルタの振幅特性
図：くし型フィルタの振幅特性

上図のようにくし型フィルタの振幅特性は平坦ではないため、カラレーションのように音色が変化してしまう欠点があります。

この音色の変化をなくすために、振幅特性が平坦なフィルタを使う必要があります。

補足：私も知りませんでしたが、論文中に出てきたカラレーション (coloration) とは以下のような現象みたいです。

カラレーション

室内で起こる音響現象の一つです。

発せられた直接音と壁などによる反射音が干渉して、音色が変化して聞こえる現象です。中・高音域で多重反射が起きている室内などで発生しやすい。

引用元：【カラレーション 】 - オーディオ辞典

エコー密度が小さい

くし型フィルタのインパルス応答を以下に示す。

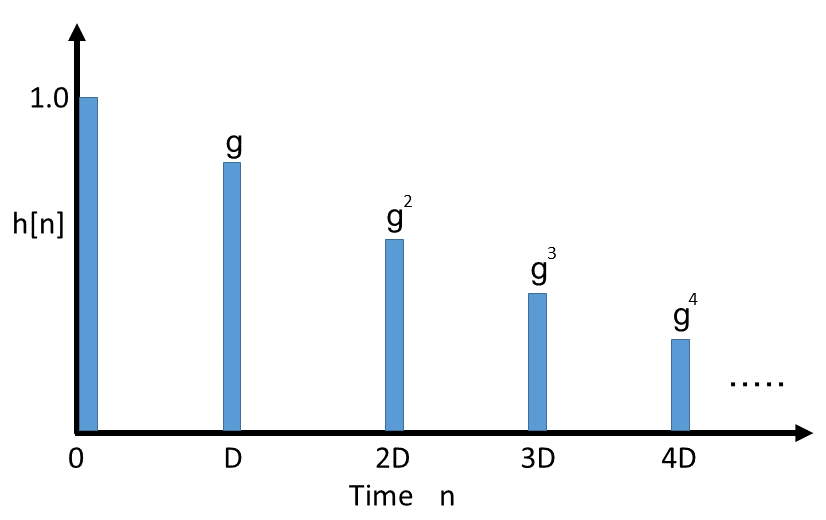
図：くし型フィルタのインパルス応答
図：くし型フィルタのインパルス応答

上図のようにサンプル番号 Ｄ ごとに値があるようなインパルス応答となっています。

遅延時間\(\ \tau\) を 40ms （サンプリング周波数 48kHzの場合、D=48x40=1920）に設定した場合、エコー密度は1000ms/40ms=25です。このエコー密度は実際の残響に比べて小さく、音がはためいているように聞こえてしまいます。

文献[1] によれば、はためきをなくすにはエコー密度が約1000必要であり、1000あればそれ以上のエコー密度のリバーブと聴き分けができないみたいです。そのため、リバーブの改善にはエコー密度を1000に近づける必要があります。

補足：「音がはためいている」は文献 [1] の"fluttering"の直訳です。

オールパスフィルタ

オールパスフィルタとオールパスフィルタでエコー密度を高める方法を説明したいと思います。

オールパスフィルタについて

オールパスフィルタとは冒頭で説明したように周波数の振幅特性を変えずに位相特性を変えるフィルタのことです。

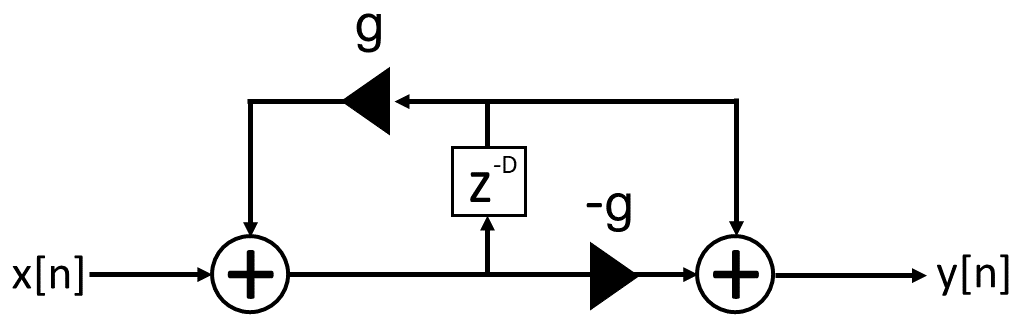
くし型フィルタの式の直接音 x[n] を\(-g \) 減衰させ、 D だけ遅延させた直接音 x[n-D] を加えることでオールパスフィルタは作成できます。

$$
\begin{align}
●& くし型フィルタ \\[5pt] &y[n] = x[n] + g y[n-D] \\[9pt] ●& オールパスフィルタ \\[5pt] &y[n] = \color{red}{-g x[n]} + \color{red}{x[n-D]} + g y[n-D] \\
\end{align}
$$

オールパスフィルタのブロック図とインパルス応答は以下です。

図：オールパスフィルタのブロック図
図：オールパスフィルタのブロック図
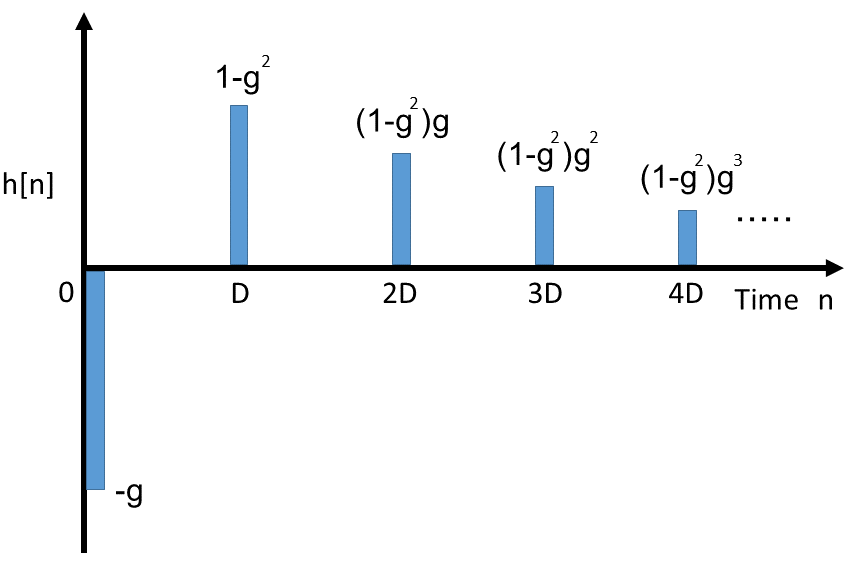
図：オールパスフィルタのインパルス応答
図：オールパスフィルタのインパルス応答

z 変換した式は以下です。

$$
H(z) = \frac{-g+z^{-D}}{1-g z^{-D}}
$$

\(z=e^{jω}\) を代入して、絶対値を計算すると以下のように振幅特性が得られます。

$$
\begin{align}
|H(\omega)| &= \frac{|-g+e^{-j\omega D}|}{|1-g e^{-j\omega D}|} \\[5pt] &= |e^{-j\omega D}|\frac{|1-g e^{j\omega D}|}{|1-g e^{-j\omega D}|} \\[5pt] &= 1 \cdot \frac{\sqrt{(1-g \cos{(\omega D)})^2+(g \sin{(\omega D)})^2}}{\sqrt{(1-g \cos{(\omega D)})^2+(g \sin{(\omega D)})^2}} \\[5pt] &= 1
\end{align}
$$

上記のように振幅特性がすべての周波数で1となっているため、このオールパスフィルタをリバーブ作成に使用します。

エコー密度を高める方法

エコー密度を高めるためにオールパスフィルタを以下のように縦続接続します。

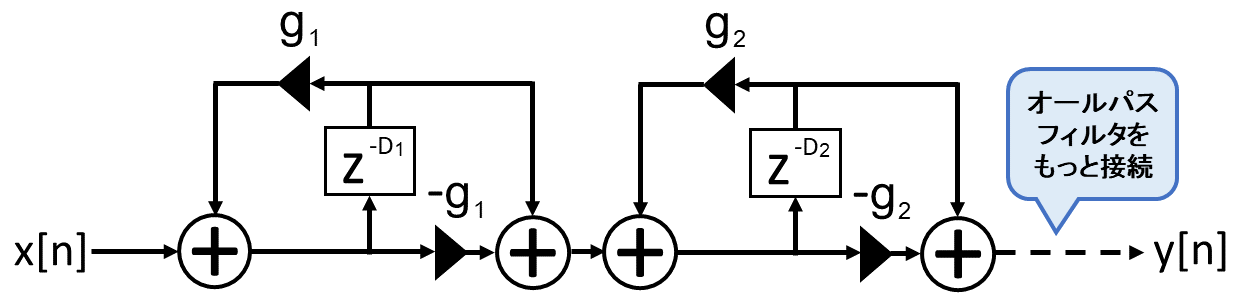
図：オールパスフィルタの縦続接続
図：オールパスフィルタの縦続接続

各オールパスフィルタの遅延時間 D2, D3, …については前の段の遅延時間の約1/3に設定します。つまり、n 段目のオールパスフィルタの遅延時間 Dn は数式で以下のように表せます。

$$
D_{n} = D_{1}\left(\frac{1}{3}\right)^{n-1} \tag{A}
$$

ただし、反射音の打ち消しや重なりが起こらないように各段の遅延時間は厳密に(A)式に従わず、微妙にずらして設定します。

このとき、エコー密度 d は以下のように表せます。

$$
d \approx \frac{3^{n-1}}{\tau_1}
$$

\(\tau_1=100\) ms、オールパスフィルタを5段接続した場合、エコー密度は約810となり、1000に十分近づきます。

各減衰率 \(g_n\) については 0.7 が良いと記載がありました。

補足：各段の遅延時間どうしは反射音の打ち消しが起こらないようにそれらの最小公倍数をなるべく大きくしたほうがよいです。一番ベストなのは互いに素となる遅延時間を使うことです。

例として、D1=4800、g=0.7、オールパスフィルタを２つ接続したときのインパルス応答を以下に示します。上図がD2=D1/3のとき、下図がD2=D1/3+1のときのインパルス応答です。

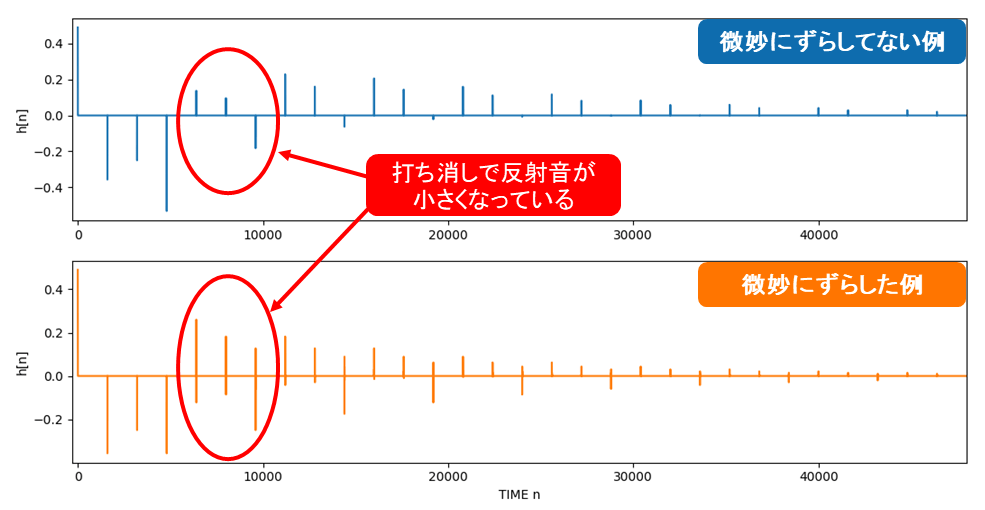
図：遅延時間を微妙にずらす理由
上図：D2 = D1/3 の例 　下図：D2 = D1/3+1 の例

図からわかるように微妙にずらしていない場合、反射音が打ち消しあい、エコー密度が小さくなっています。特に赤く示したところは顕著に小さくなっています。

このように、反射音が打ち消しあい、エコー密度も小さくなってしまいますので、遅延時間は(A)式から微妙にずらします。

プログラム

オールパスフィルタによるリバーブを適用するプログラムをPythonで実装しました。ソースコードと実行方法について説明します。

ソースコード

入力データにオールパスフィルタを5つ縦続接続したリバーブを適用するプログラムは以下です。

import soundfile as sf
import numpy as np
import scipy.signal as sg

# パラメータ
tau1 = 100    # 1段目遅延時間 [ms]
gain = 0.7    # 減衰率
unit_num = 5  # 縦続接続数
wav_in_name  = "input_short.wav"  # 入力音データ名
wav_out_name = "output_short.wav" # 出力音データ名

# WAVファイルを読み込む
x, fs = sf.read(wav_in_name)

# [ms] → [サンプル] に変換
D = [0] * unit_num
D[0] = int(tau1 * fs / 1000)
for i in range(1, unit_num):
    D[i] = D[i-1]//3+1  # 重ならないように+1してずらす

# フィルタ係数を設定
for i in range(unit_num):
    b = np.zeros(D[i]+1)
    a = np.zeros(D[i]+1)
    b[0] = -1.0*gain
    a[0] = 1.0
    a[D[i]] = -1.0*gain
    b[D[i]] = 1.0
    x = sg.lfilter(b, a, x) # リバーブをかける

# wavファイルを書き込む
y = x    
y = y/np.max(np.abs(y))   # ノーマライズ
sf.write(wav_out_name, y, fs, subtype='PCM_16')

18～19行目：2段目、3段目...の遅延時間 Dn を設定します。前の段の遅延時間の1/3に+1して、反射音の重なりが起こらないようにします。

21～29行目：オールパスフィルタの接続数だけフィルタをかけています。

33行目：オーバーフローしたときのためにノーマライズしています。

実行方法

(1) プログラムを実行するディレクトリにソースコード(allpass_reverb.py)と入力 WAV データを格納する。

(2) ソースコード5～10行目のパラメータと入出力データ名を修正する。

# パラメータ
tau1 = 100    # 1段目遅延時間 [ms]
gain = 0.7    # 減衰率
unit_num = 5  # 縦続接続数
wav_in_name  = "input_short.wav"  # 入力音データ名
wav_out_name = "output_short.wav" # 出力音データ名

(3) 以下のコマンドで python を実行することで、リバーブをかけたWAVデータが出力される。

$ python allpass_reverb.py

処理結果

以下のようにパラメータを設定して、音声にリバーブをかけました。

表：リバーブのパラメータ
パラメータ名 記号 変数名 設定値
遅延時間 \(\tau_{1}\) tau1 10 [ms]
減衰率 \(g_{n}\) gain 0.7
縦続接続数 \(N\) unit_num 5

オールパスフィルタによるリバーブをかけた音声は以下のようになります。実測のホールのインパルス応答を畳み込んだ音声も載せておきます。

入力した音声

オールパスフィルタによるリバーブを使用した音声

実測のホールのリバーブを使用した音声

オールパスフィルタによるリバーブは実測のホールのリバーブに近い雰囲気になっている気がしますね。ただし、オールパスフィルタによるリバーブは響きすぎな気もしました。

この響きがリバーブについて調べるとよく出てくる金属的な響きというやつなのでしょうか。わからんけども…。

おわりに

本記事では、オールパスフィルタによるリバーブの実装を行いました。くし型フィルタによるリバーブよりも実際の残響音に近づいたのではないかと思います。文献 [1] には更に洗練したリバーブの実装も行っていますので、今度紹介したいと思います。

■参考文献
[1] M.R.Schroeder, ”Natural Sounding Artificial Reverberation”, J.Audio Eng. Soc., vol.10, p.219, 1962．

■使用した音声について
この記事で信号処理した音声はユーフルカで提供されている音声を使用させていただきました。

【音声のページ】
ボイス素材：店員（老人男性） https://youfulca.com/2022/08/07/shop_oldman/

■使用したインパルス応答について
この記事で使用したインパルス応答は Openair で提供されている以下のインパルス応答を使用させていただきました。

・ "Central Hall, University of York" © 2015 Alexander Vilkaitis, Ilias Antonopoulos, Joska De Langen, Xuan Liu (Licensed under CC BY 4.0) https://www.openairlib.net