本記事では、くし型フィルタ(コムフィルタ)によるリバーブを実装してみました。リバーブの実装方法ではくし型フィルタによる方法が一番単純かなと思います。
リバーブ(残響)
はじめにリバーブについて説明を行い、次にリバーブの定式化、それから定式化したリバーブの周波数特性について説明したいと思います。
リバーブについて
まず、リバーブとは音に残響音を加えるエフェクタのことです。大きなホールのリバーブを使用することによって、音があたかも大きなホールで録音したような響きとなります。
リバーブを作る方法は以下の2つです。
- 実際に計測したインパルス応答を使用する方法
- 残響をモデル化する方法
実際に計測したインパルス応答を使用する方法のほうがリバーブの響きは良くなるのですが、計算量が多くなるというデメリットがあります。例えば、デジタル回路で実装する場合、乗算器と加算器が数千個から数万個必要になります。
一方、残響をモデル化したリバーブは乗算器と加算器が数十個あれば十分なため、計算量が小さいというメリットがあります。また、好きなように残響時間などを変更できるというメリットもあります。
昔は計算リソースの問題で残響をモデル化する方法しか使えなかったと思いますが、現代においても計算リソースの節約やリバーブの調整ができるというメリットがあるため、使用されている印象です。
残響のモデル化
リバーブの発生する状況の模式図を以下に示します。
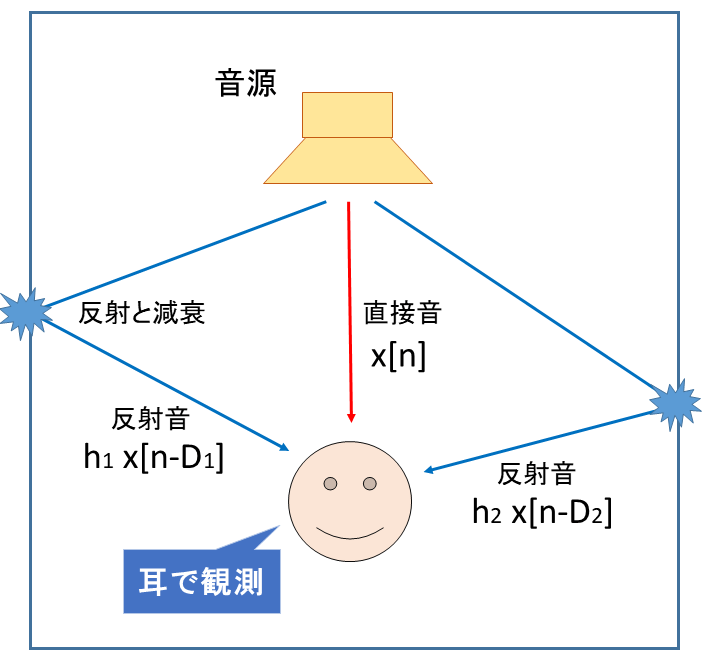
まず音源から直接音が届き、その後に壁から反射された反射音が届くように表せます。数式による表現は以下です。
$$
y[n] = x[n] + \sum_{l=1}^{L} h_{l} x[n-D_{l}]
$$
ここで\(\ L\ \)は反射音の数です。
上記のように数式で表すことができますが、反射音の数だけ遅延時間\(\ D_l\ \)と減衰率\(\ h_{l}\ \)を設定しないといけないため、扱いが難しいです。
また、FIRフィルタの場合、実測のインパルス応答を畳み込む処理と計算時間が変わらないため、モデル化してもあまり意味がありません。
そこで以下の図のように考えて、残響をモデル化します [1]。
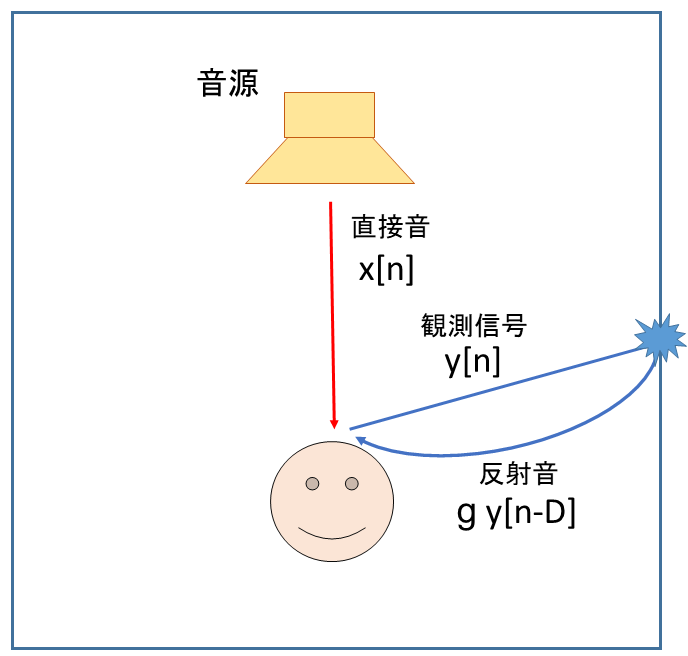
図のように観測した音が再び反射して聞こえてくるように考えます。数式で表すと以下のようになります。
$$
y[n] = x[n] + g y[n-D]
$$
リバーブのブロック図とインパルス応答は以下です。
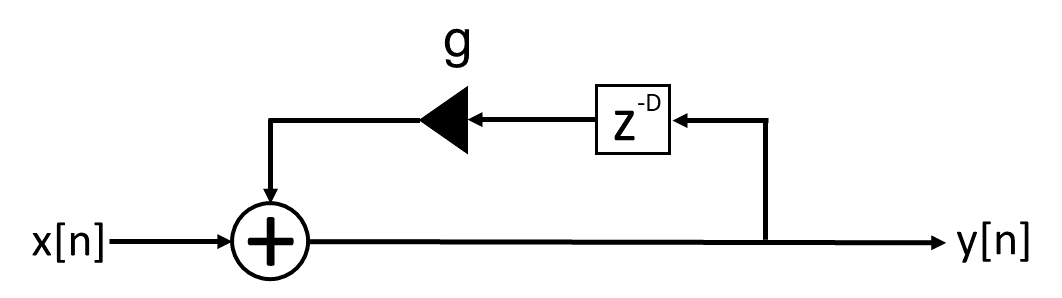
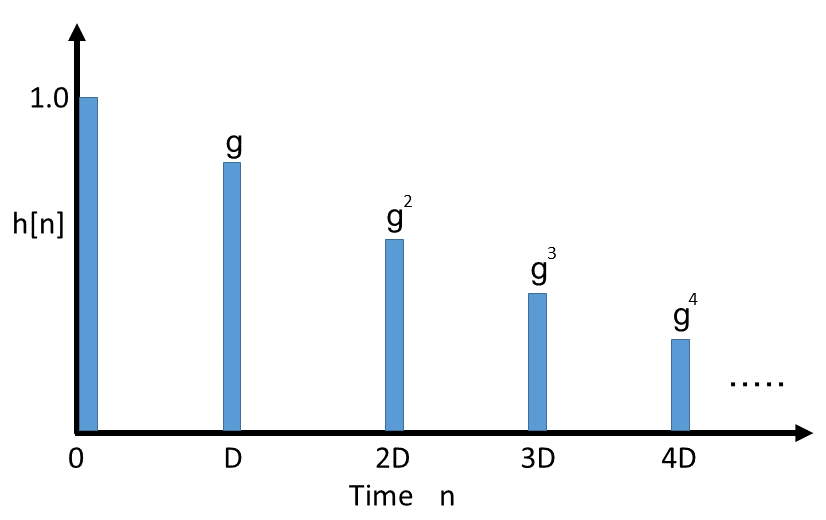
この場合、考えるパラメータは減衰率 \(g\) だけとなります。また、IIRフィルタのため、FIRフィルタより少ない計算量で実装できます。
くし型フィルタ
さきほどの計算式
$$
y[n] = x[n] + g y[n-D]
$$
の周波数特性\(\ H(\omega)\ \)を調べていきます。
式をz変換して、\(z=e^{j\omega}\)を代入すると、以下のように周波数特性が得られます。
$$
H(\omega) = \frac{1}{1-g e^{-j\omega D}}
$$
振幅特性\(|H(\omega)|\)は以下のようになります。
$$
|H(\omega)| = \frac{1}{\sqrt{(1+g^2)-2g \cos{(\omega D)}}}
$$
遅延数 D=8, 減衰率 \(g=0.5, 0.7, 0.9\) にしたときの振幅特性を以下に示します。
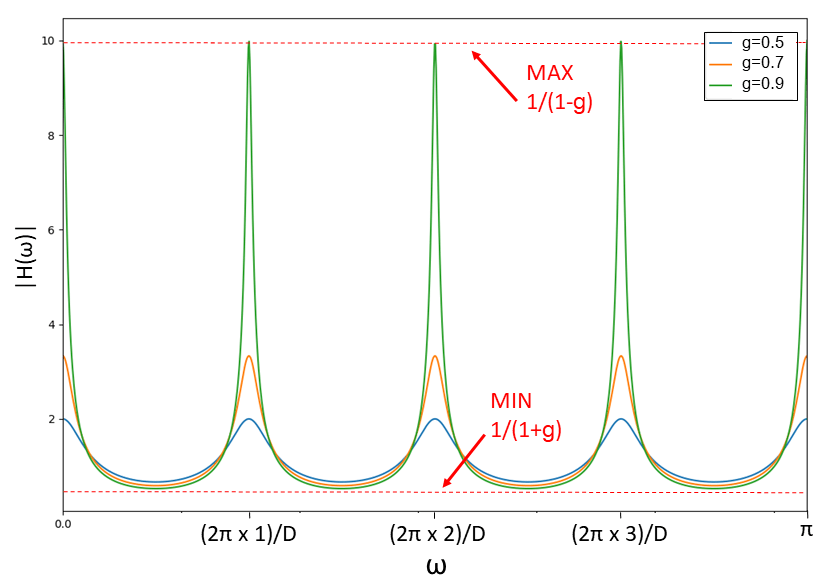
上図のように 2π/D 間隔で山があり、最大値は \(1/(1-g)\)、最小値は \(1/(1+g)\ \)となります。
振幅特性がくし型になっているので、このフィルタはくし型フィルタとよばれています。
プログラム
くし型フィルタによるリバーブをかけるプログラムをPythonで実装しました。ソースコードと実行方法について説明します。
ソースコード
入力データにくし型フィルタのリバーブを適用するソースコード comb_reverb.py は以下です。
import soundfile as sf
import numpy as np
import scipy.signal as sg
# パラメータ
tau = 40 # 遅延時間 [ms]
gain = 0.5 # 減衰率
wav_in_name = "input.wav" # 入力音データ名
wav_out_name = "output.wav" # 出力音データ名
# WAVファイルを読み込む
x, fs = sf.read(wav_in_name)
# [ms] → [サンプル] に変換
D = int(tau * fs / 1000)
# フィルタ係数を設定
b = np.zeros(D+1)
a = np.zeros(D+1)
b[0] = 1.0
a[0] = 1.0
a[D] = gain
# リバーブをかける
y = sg.lfilter(b, a, x)
# wavファイルを書き込む
y = y/np.max(np.abs(y)) # ノーマライズ
sf.write(wav_out_name, y, fs, subtype='PCM_16') 6行目:遅延時間\(\ \tau\ \) [ms] を設定します。
15行目:遅延時間 \(\ \tau\ \) [ms] から遅延サンプル数 D に変換しています。
28行目:オーバーフローしたときのためにノーマライズしています。
実行方法
(1) プログラムを実行するディレクトリにソースコード(comb_reverb.py)と入力 WAV データを格納する。
(2) ソースコード6~9行目のパラメータと入出力データ名を修正する。
# パラメータ
tau = 40 # 遅延時間 [ms]
gain = 0.5 # 減衰率
wav_in_name = "input.wav" # 入力音データ名
wav_out_name = "output.wav" # 出力音データ名
(3) 以下のコマンドで python を実行することで、リバーブをかけたWAVデータが出力される。
$ python comb_reverb.py処理結果
以下のようにパラメータを設定して、音声にリバーブをかけました。
| パラメータ名 | 記号 | 変数名 | 設定値 |
|---|---|---|---|
| 遅延時間 | \(\tau\) | tau | 40 [ms] |
| 減衰率 | \(g\) | gain | 0.5 |
くし型フィルタによるリバーブをかけた音声は以下のようになります。
入力した音声
リバーブをかけた音声
お風呂に入ったときのような声となっており、残響をうまく表現できているのではないかと思います。しかし、電子的な音がしており、自然な残響ではない感じがしますね。
おわりに
本記事では、くし型フィルタによるリバーブの説明と実装を行いました。単純な方法でしたが、実際の残響に似ているのではないかと思います。ただし、自然な残響に近づけるためにもう少し改善が必要かなと感じます。
■参考文献
[1] 川村新、”音声音響信号処理の基礎と実践”、コロナ社、2021.
■使用した音声について
この記事で信号処理した音声はユーフルカで提供されている音声を使用させていただきました。
【音声のページ】
ボイス素材:店員(老人男性) https://youfulca.com/2022/08/07/shop_oldman/
■変更履歴
・2025/02/21:記事の文言の変更
