本記事では窓関数法による FIR フィルタ設計を紹介します。
個人的にフィルタ設計の方法では一番単純な設計方法ではないかと思います。
窓関数法の流れ
窓関数法の流れは以下のようになります。
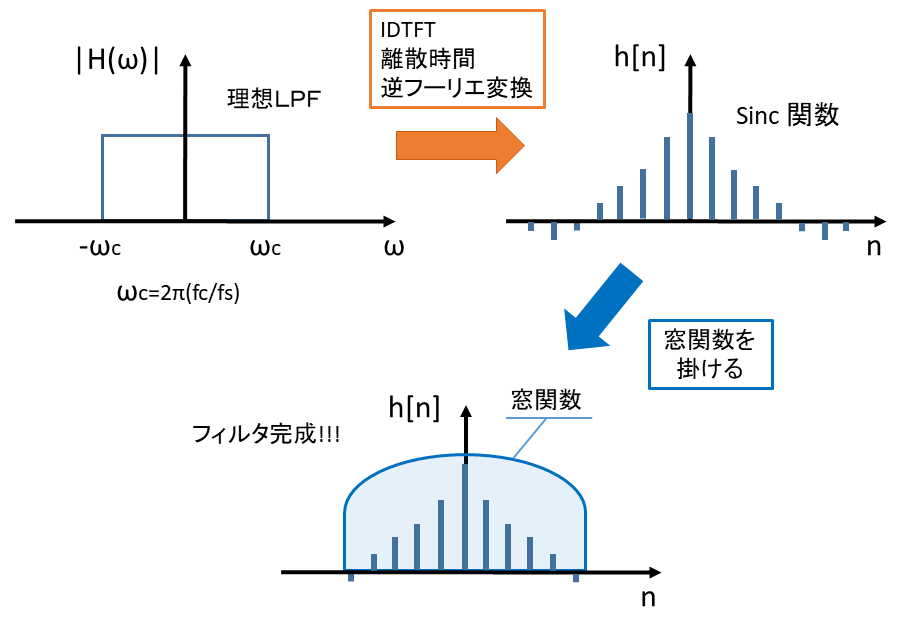
まず、カットオフ周波数を fc とした理想低域通過フィルタ(LPF)を作成します。
その理想 LPF に対して離散時間逆フーリエ変換(IDTFT)を行い、無限長のインパルス応答を求めます。
無限長のインパルス応答に窓関数を掛けて、有限長のフィルタを作成するというのが窓関数法の流れとなります。
補足:離散時間逆フーリエ変換は以下の式となります。
$$
h[n] = \frac{1}{2\pi} \int_{-\pi}^{\pi} H(\omega) e^{j\omega n} d\omega
$$
窓関数法の考え方
理想 LPF のインパルス応答を単純に有限長(-M ≦ n ≦ M)に打ち切った場合、その周波数特性は以下のようになります。
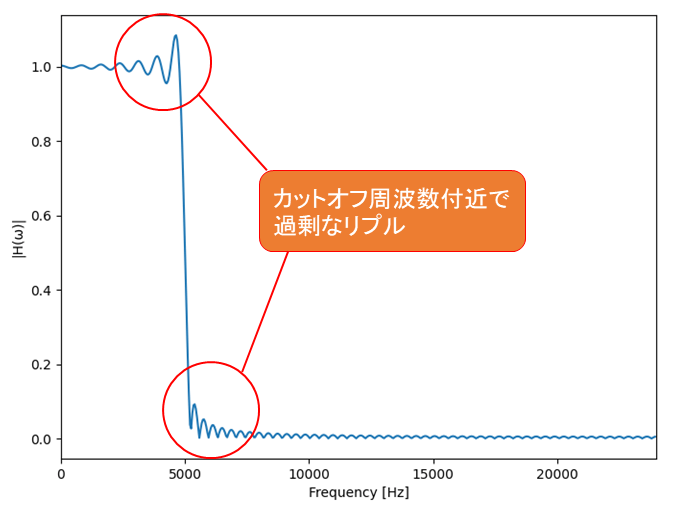
上図のようにカットオフ周波数付近で振幅特性が波打っています。この振幅のことはリプルと呼ばれており、もちろん小さい方がよいです。
このリプルの原因は、n=M+1 における急なインパルス応答の消失のため、窓関数を乗算して滑らかにインパルス応答が消失するようにします。
FIR フィルタ設計手順
窓関数法による FIR フィルタ設計手順は以下です。
- カットオフ周波数が fc [Hz] となる理想 LPF のインパルス応答を求める。
- 理想 LPF のインパルス応答に窓関数を乗算。
- HPFなどを作成する場合は周波数シフトする。
- 作成したフィルタの周波数特性を確認する。
理想 LPF のインパルス応答
カットオフ周波数 fc [Hz]、サンプリング周波数 fs [Hz] のとき、理想 LPF のインパルス応答\(h_{ideal}\)は以下のように求まります。
$$
\begin{align}
h_{ideal}[n] &= \frac{1}{2\pi} \int_{-\pi}^{\pi} H_{ideal}(\omega) e^{j\omega n} d\omega \\[5pt]
&= \frac{1}{2\pi} \int_{-\omega_c}^{\omega_c} e^{j\omega n} d\omega \\[5pt]
&= \frac{1}{2\pi} \left[\frac{1}{jn}e^{j\omega n} \right]_{-\omega_c}^{\omega_c} \\[5pt]
&= \frac{1}{\pi n} \frac{(e^{j\omega_c n} - e^{-j\omega_c n})}{2j} \\[5pt]
&= \frac{1}{\pi n} \sin{(\omega_c n)} \\[5pt]
&= 2\frac{f_c}{f_s} \frac{\sin{(\omega_c n)}}{\omega_c n} \tag{A}
\end{align}
$$
ここで、
$$
\frac{\sin{(\omega_c n)}}{\omega_c n} = {\rm sinc}(\omega_c n)
$$
はシンク関数と呼ばれ、理想 LPF のインパルス応答は以下のようになります。
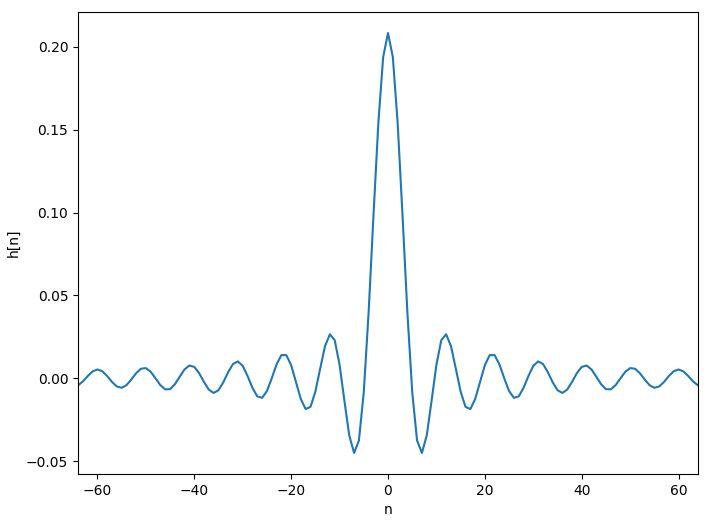
補足:n=0 のときは sinc(0)=0/0 となり、プログラムでは(A)式が計算できないため、sinc(0)=1 として計算する必要があります 。
窓関数を乗算
窓関数はいくつかありますが個人的によく見るのはハニング窓です。
ハニング窓は次式で定義されます。
$$
w=0.5+0.5\cos{\left(\frac{\pi n}{M}\right)}
$$
ハニング窓の形と乗算後のインパルス応答は以下のようになります。
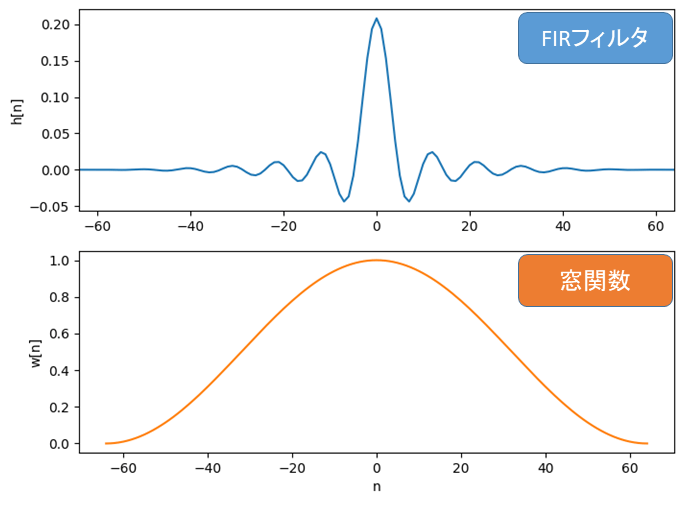
ひどまず、これで FIR フィルタ(LPF)の完成です。
補足:今の状態ですと未来の入力が過去の出力に影響を与えないという因果性を満たしていないです。因果性を満たすために作成したインパルス応答を M だけ右にシフトする必要があります。
オフライン処理の場合は因果性を満たしていなくても問題ないと思いますが、この記事では因果性を満たすようにします。
周波数シフト(変調)
ハイパスフィルタ(HPF) や バンドパスフィルタ(BPF)を作る場合は、周波数シフトを使って作成します。
フーリエ変換の性質として以下のような周波数シフトの性質があります。
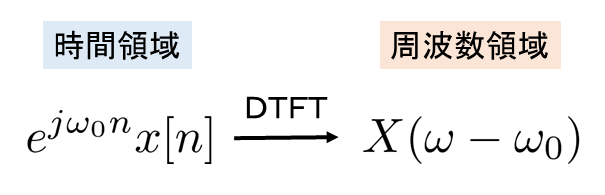
この性質を利用すると以下のようにすることで HPF を作成することができます。
$$
\begin{align}
h_{\rm HPF}[n] &= h_{\rm LPF}[n] \cos(\pi n) \\[5pt]
&= h_{\rm LPF}[n] \frac{e^{j\pi n}+e^{-j\pi n}}{2}
\end{align}
$$
これで HPF ができる理由としては、デジタルにおける周波数領域では図のように周波数シフトがされるためです。
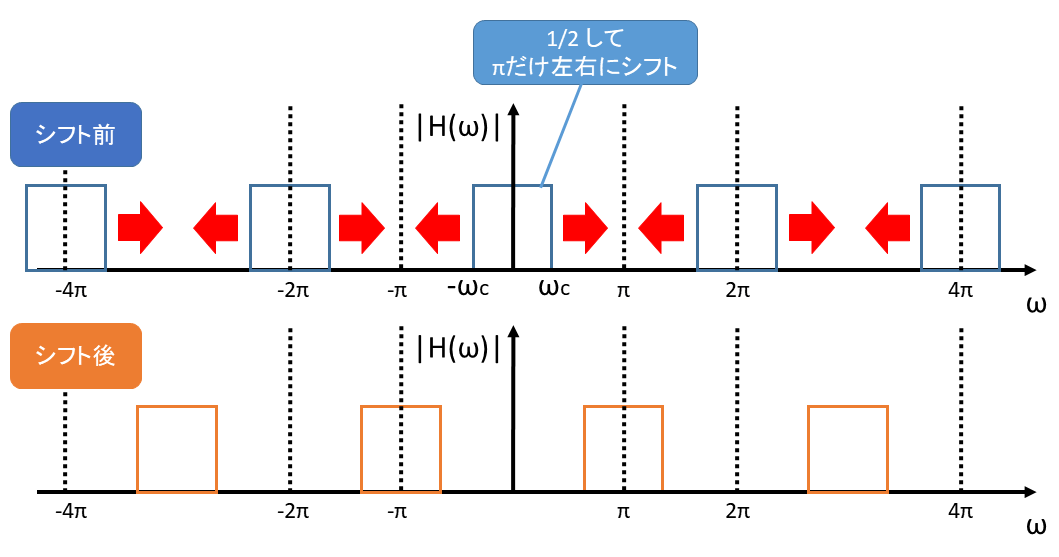
また、BPF の場合は以下のようにします。
$$
\begin{align}
h_{\rm BPF}[n] &= 2h_{\rm LPF}[n] \cos(\omega_o n) \\[5pt]
&= h_{\rm LPF}[n] (e^{j\omega_o n}+e^{-j\omega_o n})
\end{align}
$$
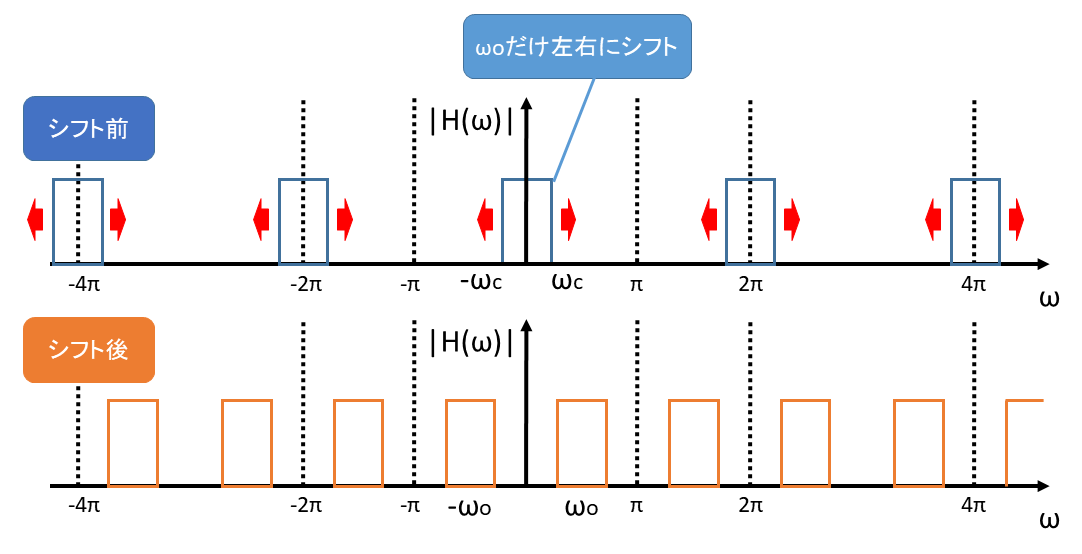
カットオフ周波数については周波数シフトにより変わってしまうため、LPF以外のフィルタを作成する場合はあらかじめカットオフ周波数が変化することを考慮する必要があります。
周波数特性の確認
作成したフィルタの周波数特性が問題ないか確認いたします。
周波数特性の確認は以下のように離散時間フーリエ変換(DTFT)をすることで確認できます。
$$
H(\omega) = \sum_{n=-\infty}^{\infty}h[n]e^{-j\omega n}
$$
fc=5kHz、fs=48kHz、M=64のときの矩形窓とハニング窓の周波数特性は以下のようになります。
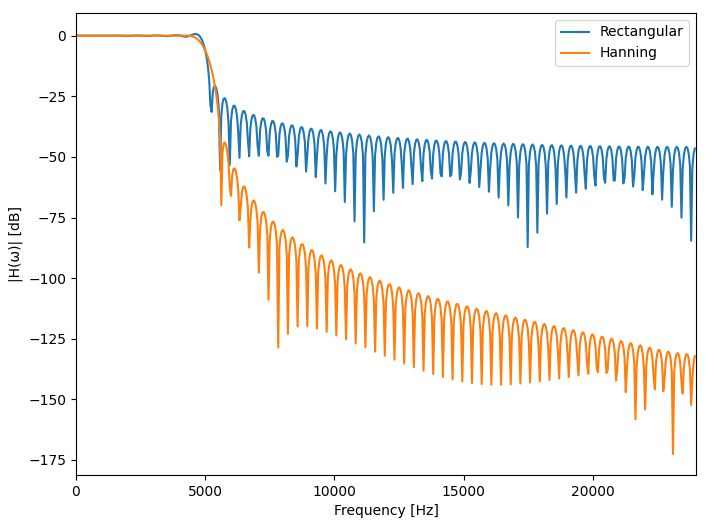
ハニング窓のほうが矩形窓よりもリプルが小さいのがわかると思います。
周波数特性を見て納得いかなければ、次数 M や窓関数を変えて、FIR フィルタを作り直します。
矩形窓:矩形窓というのは単純に有限長で区切る窓関数です。
$$
\begin{equation}
w[n] =
\left\{
\begin{array}{ll}
1 & (-M \leq n \leq M) \\
0 & (n < -M, M < n)
\end{array}
\right.
\end{equation}
$$
対数表示:人間の感覚量は受ける刺激の強さの対数に比例するというウェーバー・フェヒナーの法則があるため、フィルタの周波数特性は基本的に対数表示します。
プログラム
窓関数法によるFIRフィルタを畳み込むプログラムをPythonで実装しました。ソースコードと実行方法について説明します。
ソースコード
窓関数法によるFIRフィルタ(LPF)を畳み込むソースコード window_func.py は以下です。
import soundfile as sf
import numpy as np
import scipy.signal as sg
# パラメータ
fc = 5000 # カットオフ周波数 [Hz]
M = 64 # 次数
window = sg.windows.hann(2*M+1) # 窓関数
wav_in_name = "input.wav" # 入力WAVデータ名
wav_out_name = "output.wav" # 出力WAVデータ名
# WAVファイルを読み込む
x, fs = sf.read(wav_in_name)
omega_c = 2.0 * np.pi * (fc/fs)
# 理想低域通過フィルタ
m = np.arange(1,M+1)
h_ideal = np.zeros(2*M+1)
h_ideal_half = 2 * (fc/fs) * np.sin(omega_c * m) / (omega_c * m)
h_ideal[0:M] = h_ideal_half[::-1]
h_ideal[M] = 2 * (fc/fs)
h_ideal[M+1:2*M+1] = h_ideal_half
# 窓関数を乗算
h = h_ideal * window
# インパルス応答を畳み込む
y = sg.convolve(x, h)
# 入力と出力の大きさをそろえる
length = len(x)
y = y[0:length]
# WAVファイルを書き込む
sf.write(wav_out_name, y, fs, subtype='PCM_16')
19~20行目:19行目で理想 LPF の半分だけ作成して、20行目でそれを逆順にコピーしています。
21行目:sinc(0)=1 として、h[M]=2(fc/fs) を格納。
実行方法
(1) プログラムを実行するディレクトリにソースコード(window_func.py)と入力 WAV データを格納する。
(2) ソースコード5~10行目のパラメータと入出力データ名を修正する。
# パラメータ
fc = 5000 # カットオフ周波数 [Hz]
M = 64 # 次数
window = sg.windows.hann(2*M+1) # 窓関数
wav_in_name = "input.wav" # 入力WAVデータ名
wav_out_name = "output.wav" # 出力WAVデータ名
(3) 以下のコマンドで python を実行することで、FIRフィルタをたたみ込んだ WAV データが出力される。
$ python window_func.py処理結果
以下のようにパラメータを設定して、音声に対して窓関数法によるFIRフィルタを畳み込みました。
| パラメータ名 | 変数名 | 設定値 |
|---|---|---|
| カットオフ周波数 | fc | 5000 [Hz] |
| 次数 | M | 64 |
| 窓関数 | window | ハニング窓 |
窓関数法によるFIRフィルタの効果は以下のようになります。
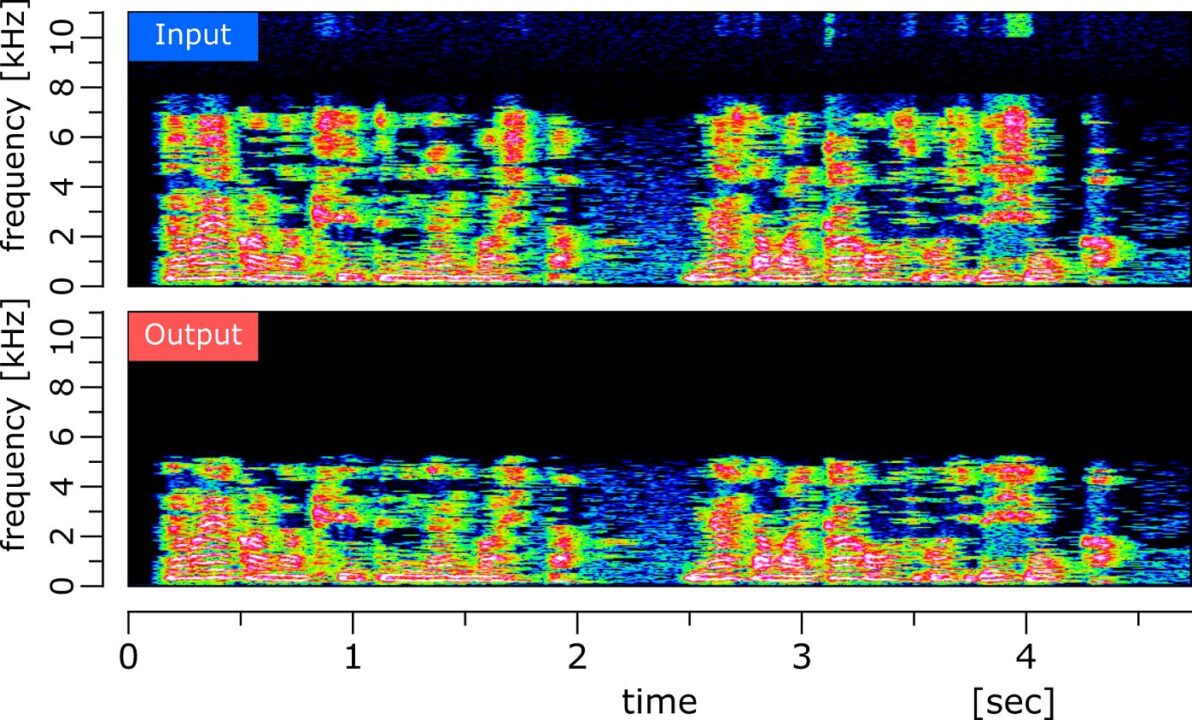
綺麗に 5kHz で周波数成分がなくなっており、フィルタの効果がわかると思います。
おわりに
本記事では窓関数法による FIR フィルタ設計を紹介しました。
周波数シフトによる HPF や BPF の作成は文献にはあまり載っていないですが、個人的にはこれがわかりやすい作り方だと思い紹介しました。
本記事がデジタル信号処理学習者の助けになれば幸いです。
参考文献
[1] 陶山 健仁、”ディジタルフィルタ原理と設計法”、科学情報出版株式会社、2018.
[2] 尾知 博、”ディジタル・フィルタ設計入門 各種フィルタの原理”、CQ出版社、1990.
■変更履歴
・2025/01/30:タグの変更
