ねっちゅう工房

双一次変換によるIIRフィルタ設計

カットオフ周波数を決めれば、単純な計算だけでIIRフィルタの係数が求まる方法はないかと思っていたら、双一次変換と呼ばれる方法があったので紹介します。

目次

双一次変換によるIIRフィルタ設計手順

双一次変換によるIIRフィルタの設計手順は以下です。

  1. アナログ基準ローバスフィルタを設計する。
  2. 周波数変換で所望のカットオフ周波数\(\ \omega_c\) にする。
  3. アナログフィルタに双一次変換を行い、 \(H(z)\)を求める。

今回は手始めに以下のような2次のIIRフィルタの伝達関数を作ります。

$$H(z) = \frac{b_0+b_1z^{-1}+b_2z^{-2}}{a_0+a_1z^{-1}+a_2z^{-2}}$$

アナログ基準ローバスフィルタの設計

カットオフ角周波数が \(\omega_c=1\) であるローバスフィルタ（LPF）を基準LPFと呼び、最初にアナログ基準LPFの伝達関数を設計します。

補足：デジタル信号処理の世界では暗黙のうちに周波数 \(f'\) をサンプリング周波数 \(f_s\) で割った正規化周波数 \(f'/f_s\) を周波数 \(f\) と呼ぶことがあります。同様に角周波数についても正規化角周波数 \(2\pi f'/f_s\) を角周波数 \(\omega\) と呼ぶことがありますので気をつけて下さい。この記事でも正規化角周波数 \(2\pi f'/f_s\) を角周波数 \(\omega\) と呼びます。

STEP1

アナログフィルタの設計では \(s=j\omega\) を代入して以下の理想LPFの周波数特性 \(H_{ideal}\) に近似する有理関数 \(H(s)\) を求めます。

$$
H_{ideal}(\omega) =
\begin{cases}
1 & (\omega \lt 1) \\
0 & (\omega \geq 1)
\end{cases}
$$

有理関数というのは以下のように表せる関数です。

$$
H(s) = \frac{b_0s^m+b_1s^{m-1}+\cdots+b_m}{s^{n}+a_1s^{n-1}+\cdots + a_n}
$$

直接周波数特性を近似するのは難しい（周波数特性は複素数になる）ので、まず理想の2乗振幅特性\( |H_{ideal}(\omega)|^2\)を有理関数で近似します。アナログフィルタの代表であるバタワースフィルタの2乗振幅特性\( |H_n(\omega)|^2\)は以下になります。

$$
|H_n(\omega)|^2 = \frac{1}{1+\omega^{2n}}
$$

周波数特性をみると、確かに理想LPFに近い特性となっています。

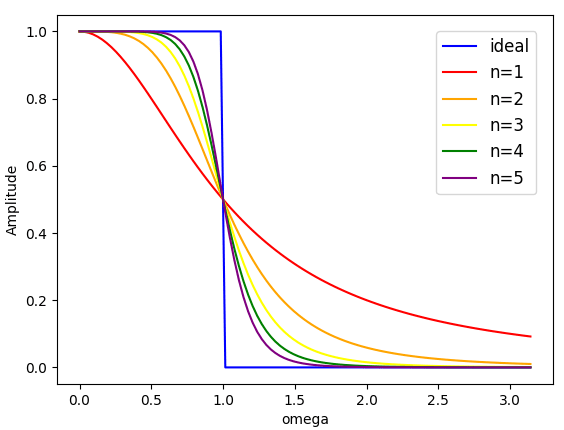
図：バタワースフィルタの周波数特性
図：バタワースフィルタの周波数特性

今回はこの有理関数 \( 1/(1+\omega^2)\ \)を使いたいと思います。（バタワースフィルタを使えばよいのですが、回りくどいことをしています。）

STEP2

2乗振幅特性は有理関数で表せたので、つぎに伝達関数\(\ H(s)\ \)を求めていきます。

\(|H_n(\omega)|^2\) の平方根を求めて\(\ \omega=s/j\ \) と置き換えればいいと思いますが、有理関数にならないので工夫が必要です。

\(|H_n(\omega)|^2\) が以下のように表せることを利用します。

$$
\begin{align}
|H_n(\omega)|^2 &= H_n(\omega) H_n^{*}(\omega) \\[5pt] &= H_n(\omega) H_n(-\omega)
\end{align}
$$

\(H_n^{*}(\omega)=H_n(-\omega)\) は実数をフーリエ変換したときの性質となっています。この性質がないと周波数特性を逆フーリエ変換した結果が複素数になってしまいます。

\(|H_n(\omega)|^2\) に \(\ \omega=s/j\) を代入すると、

$$
\begin{align}
|H_n(s)|^2 &= \frac{1}{1+(s/j)^{2n}} \\
&= \frac{1}{1+(-1)^n s^{2n}}
\end{align}
$$

\( |H_n(s)|^2\) の極を求めてみると、

n が奇数のときは

$$
\begin{align}
1 - s^{2n} &= 0 \\[5pt] s &= e^{j2\pi k/2n}
\end{align}
$$

n が偶数のときは

$$
\begin{align}
1 + s^{2n} &= 0 \\[5pt] s &= e^{j(2k+1)\pi/2n}
\end{align}
$$

以上から n=2、n=3のときの\(|H_n(s)|^2\) の極の位置は以下のようになります。

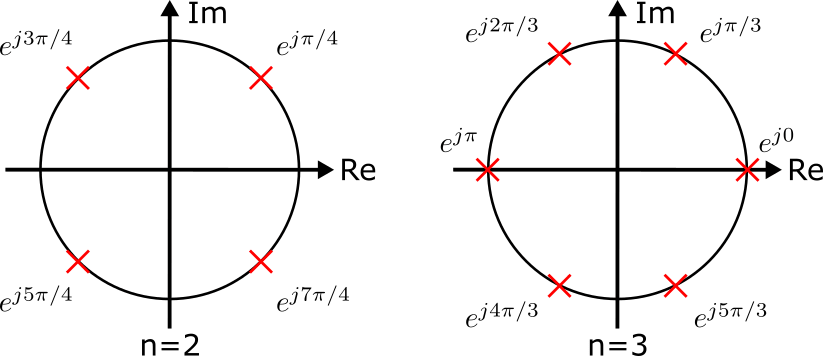
図：バタワースフィルタの2乗振幅特性の極の位置
図：\(|H_n(s)|^2\)の極の位置

\(|H(s)|^2=H(s)H(-s)\) という条件があるので、この条件を満たすように\( H(s)\) の極を選ぶ必要があります。この条件によって原点に対して対称となるペアは一方の極しか選ぶことができません。

加えて、安定なフィルタを設計するには s 平面の左半平面に極が位置する必要があるので、２つの条件を満たす\( H(s)\) の極は左半平面にある極全部となります。

したがって、n=2のときの伝達関数\(H_2(s)\) は以下のようになります。

$$
\begin{align}
H_2(s) &= \frac{1}{(s-e^{j3\pi/4})(s-e^{j5\pi/4})} \\
&= \frac{1}{s^2+\sqrt{2}s + 1}
\end{align}
$$

n=1 のときの伝達関数 \(H_1(s)\) も求めてみると以下のようになります。

$$
H_1(s) = \frac{1}{s+1}
$$

これで、 アナログ基準 LPF の設計ができました。

周波数変換

フィルタのタイプは図のように４つあります。

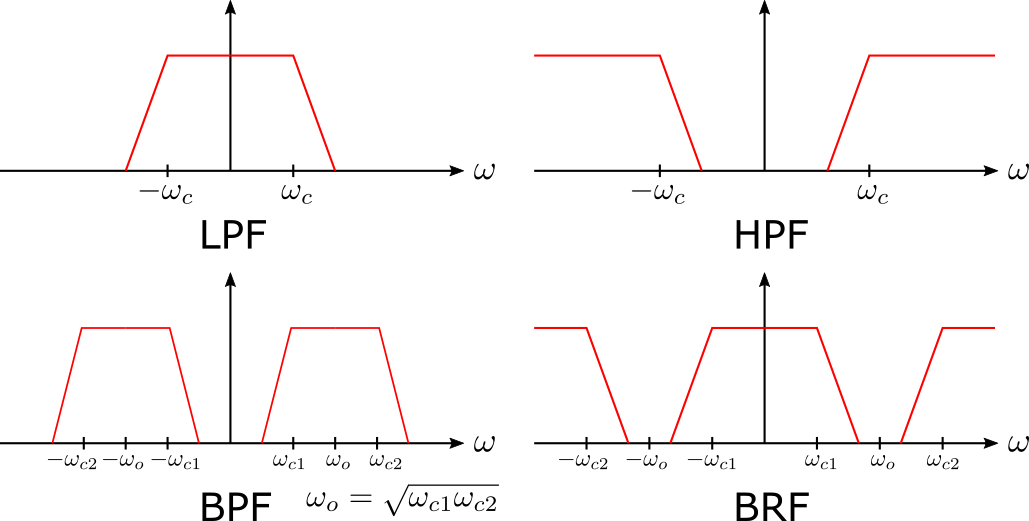
図：４つのフィルタのタイプ
図：４つのフィルタのタイプ

カットオフ角周波数が\(\ \omega_c\) である各タイプのフィルタを設計したい場合は表のように s を変換すればよいです。

表：各フィルタの s の変換
フィルタ 変換
LPF \(s\rightarrow \cfrac{s}{\omega_{c}}\)
HPF \( s\rightarrow \cfrac{\omega_c}{s}\)
BPF \( s\rightarrow \cfrac{s^2+\omega_{o}^2}{s\omega_{b}}\)
BRF \(s\rightarrow \cfrac{s\omega_{b}}{s^2+\omega_{o}^2}\)

ここで、\( \omega_b=\omega_{c2}-\omega_{c1}\) です。

\(H_2 (s)\) に対して以上のLPF変換、HPF変換すると以下のようになります。

$$
\newcommand{sb}[1]{_{#1}}
\begin{align}
H\sb{LPF}(s) &= \frac{\omega\sb{c}^2}{s^2+\sqrt{2}\ \omega\sb{c} s + \omega\sb{c}^2} \\[5pt] H\sb{HPF}(s) &= \frac{s^2}{s^2+\sqrt{2}\ \omega\sb{c} s + \omega\sb{c}^2}
\end{align}
$$

また、\(H_1 (s)\) に対して以上のBPF変換、BRF変換すると以下のようになります。

$$
\newcommand{sb}[1]{_{#1}}
\begin{align}
H\sb{BPF}(s) &= \frac{\omega\sb{b} s}{s^2+\omega\sb{b} s + \omega\sb{o}^2} \\[5pt] H\sb{BRF}(s) &= \frac{s^2+\omega\sb{o}^2}{s^2+\omega\sb{b} s + \omega\sb{o}^2}
\end{align}
$$

双一次変換

双一次変換は s 変数を以下の式で z 変数にする変換をいいます。

$$
s=2\frac{1-z^{-1}}{1+z^{-1}}
$$

このとき、図のようにアナログ角周波数 \( \omega_a : [-\infty, \infty]\) と デジタル角周波数 \(\omega_d : [-\pi, \pi]\) が対応するようになっています。

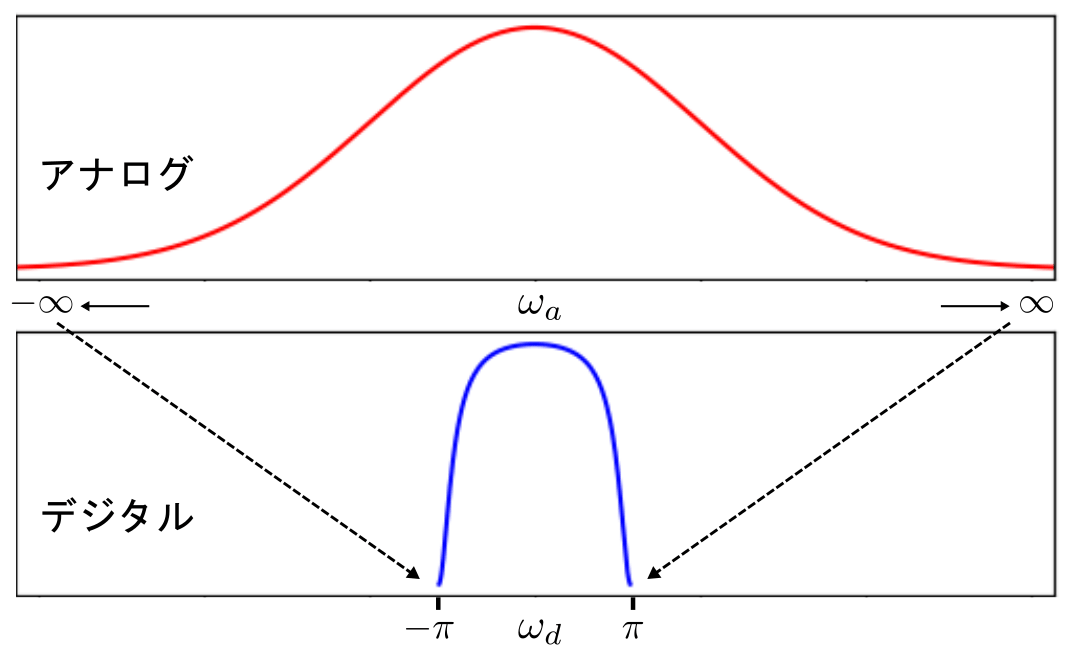
図：双一次変換による周波数の対応
図：双一次変換による周波数の対応

双一次変換の式に、\( s=j\omega_a \)、\( z=e^{j\omega_d}\) を代入すると関係式が以下のようにわかります。

$$
\newcommand{sb}[1]{_{#1}}
\omega\sb{a}=2 \tan{\frac{\omega\sb{d}}{2}}
$$

バタワースフィルタの伝達関数を双一次変換することで、\( H(z)\) を得ることができます。ただし、双一次変換によりカットオフ周波数の位置もずれてしまうため、アナログフィルタ設計の時点で予め考慮する必要があります。

\( \omega_a\) と \( \omega_d\) の関係式より、デジタルフィルタのカットオフ角周波数を \( \omega_c\) としたいときは、アナログフィルタの設計時ではカットオフ角周波数を以下の\( \ \omega'_c\) にすればよいです。

$$
\newcommand{sb}[1]{_{#1}}
\omega'\sb{c}=2 \tan{\frac{\omega\sb{c}}{2}}
$$

このことをプリワーピングと呼びます。

フィルタ係数の決定

双一次変換をバタワースフィルタの伝達関数に行った結果、各フィルタ係数は以下のようになります。\( \omega_c\) はプリワーピング後のカットオフ角周波数です。

表：LPFのフィルタ係数
\( b_0\) \( \omega_c^2\)
\( b_1\) \(2\omega_c^2\)
\(b_2\) \(\omega_c^2\)
\(a_0\) \(\omega_c^2+2\sqrt{2}\omega_c+4\)
\(a_1\) \(2\omega_c^2-8\)
\(a_2\) \(\omega_c^2-2\sqrt{2}\omega_c+4\)
表：HPFのフィルタ係数
\(b_0\) \(4\)
\(b_1\) \(-8\)
\(b_2\) \(4\)
\(a_0\) \(\omega_c^2+2\sqrt{2}\omega_c+4\)
\(a_1\) \(2\omega_c^2-8\)
\(a_2\) \(\omega_c^2-2\sqrt{2}\omega_c+4\)
表：BPFのフィルタ係数
\(b_0\) \( 2\omega_b\)
\( b_1\) \( 0\)
\(b_2\) \(-2\omega_b\)
\(a_0\) \(\omega_o^2+2\omega_b+4\)
\(a_1\) \( 2\omega_o^2-8\)
\(a_2\) \(\omega_o^2-2\omega_b+4\)
表：BRFのフィルタ係数
\(b_0\) \(\omega_o^2+4\)
\(b_1\) \(2\omega_o^2-8\)
\(b_2\) \(\omega_o^2+4\)
\(a_0\) \(\omega_o^2+2\omega_b+4\)
\(a_1\) \(2\omega_o^2-8\)
\(a_2\) \(\omega_o^2-2\omega_b+4\)

プログラム

Pythonで記述したIIRフィルタの係数と周波数特性を求めるプログラムは以下です。

import numpy as np
import scipy.signal as sg
import matplotlib.pyplot as plt
import sys

# コマンドラインの引数を取得
args = sys.argv
if len(args)!=4:
    print("\nusage: python main.py  fs  fc  type")
    print("   fs        : sampling frequency")
    print("   fc        : cutoff frequency")
    print("   type      : filter type (lpf, hpf, bpf, brf)")
    raise Exception("Argument error ")

fs = int(args[1])    # サンプリング周波数
fc = float(args[2])  # カットオフ周波数
ftype = args[3]      # フィルタの種類　LPF, HPF, BPF, BRF
fb = 5000            # バンドパスの幅

omega_b  = 2*np.pi*(fb/fs)  # バンドパスの幅
omega_c  = 2*np.pi*(fc/fs)    # カットオフ正規化角周波数
omega_c  = 2*np.tan(0.5*omega_c)  # プリワーピング
omega_c1 = omega_c-0.5*omega_b
omega_c2 = omega_c+0.5*omega_b
omega_o  = np.sqrt(omega_c1*omega_c2) 
a = [0,0,0]
b = [0,0,0] 

# フィルタ係数決定
if(ftype=="lpf"):
    b[0] = omega_c**2
    b[1] = 2*omega_c**2
    b[2] = omega_c**2
    a[0] = omega_c**2+2*np.sqrt(2)*omega_c+4
    a[1] = 2*omega_c**2-8
    a[2] = omega_c**2-2*np.sqrt(2)*omega_c+4
elif(ftype=="hpf"):
    b[0] = 4
    b[1] = -8
    b[2] = 4
    a[0] = omega_c**2+2*np.sqrt(2)*omega_c+4
    a[1] = 2*omega_c**2-8
    a[2] = omega_c**2-2*np.sqrt(2)*omega_c+4
elif(ftype=="bpf"):
    b[0] = 2*omega_b
    b[1] = 0
    b[2] = -2*omega_b
    a[0] = omega_o**2+2*omega_b+4
    a[1] = 2*omega_o**2-8
    a[2] = omega_o**2-2*omega_b+4
else: # brf
    b[0] = omega_o**2+4
    b[1] = 2*omega_o**2-8
    b[2] = omega_o**2+4
    a[0] = omega_o**2+2*omega_b+4
    a[1] = 2*omega_o**2-8
    a[2] = omega_o**2-2*omega_b+4

# 周波数特性の出力
w, h = sg.freqz(b, a)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(w, np.abs(h), c="red")
ax.set_ylim([0,1.2])
ax.set_xlabel("omega") 
ax.set_ylabel("Amplitude [dB]")
fig.savefig(ftype+".png")

以下のようにコマンドを実行することで、サンプリング周波数 fs=48kHz、カットオフ周波数 fc=12kHz の LPF のフィルタ係数と振幅特性が求まります。BPF や BRF を指定したときはバンド幅は 5kHz で、第二引数の値がバンドの中心となります。

python main.py 48000 12000 lpf

周波数特性について

サンプリング周波数 fs=48kHz、カットオフ周波数 fc=12kHz を指定してさきほどのプログラムを実行した結果、図のような特性になりました。

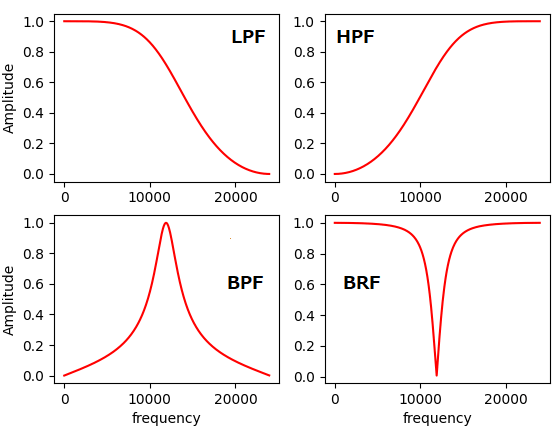
図：作成したフィルタの振幅特性
図：作成したフィルタの振幅特性

あまり急峻な特性ではないですが、２次の IIR フィルタなので仕方ないですかね。

白色雑音に対して各フィルタを畳み込んだときのスペクトログラムは図のようになります。

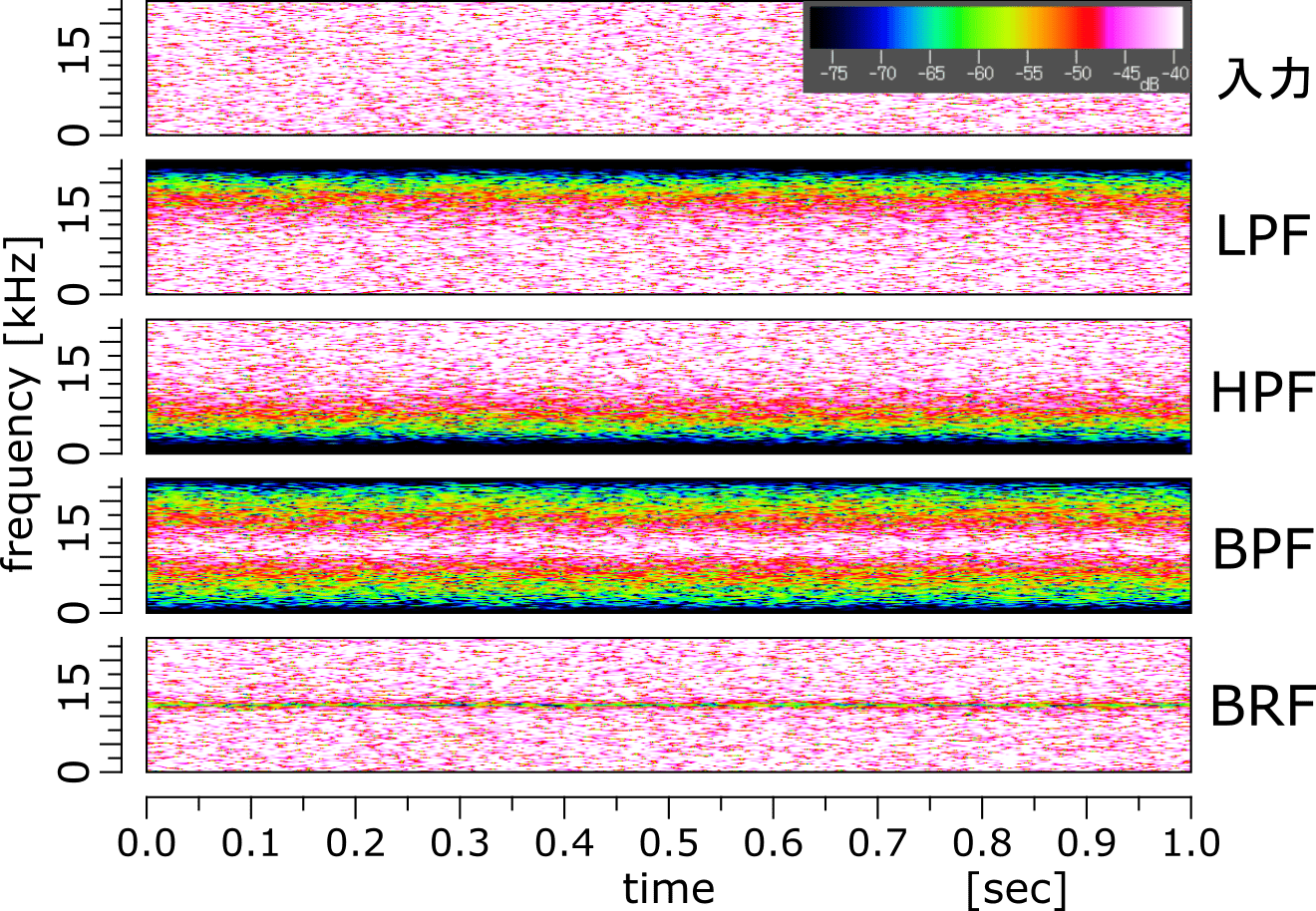
図：フィルタを畳み込んだ白色雑音のスペクトログラム
図：フィルタを畳み込んだ白色雑音のスペクトログラム

やはり急峻ではないですが、上手く機能しているのがわかると思います。

おわりに

長くなりましたが、双一次変換によるIIRフィルタ設計についてまとめました。FPGAでフィルタを作成するときなどに利用しようと思います。

参考文献
[1] 陶山 健仁、”ディジタルフィルタ原理と設計法”、科学情報出版株式会社、2018．
[2] 尾知 博、”ディジタル・フィルタ設計入門 各種フィルタの原理とCQ出版社、1990．