ウィーナーフィルターによるノイズ除去を試してみました。
いくつかの音声信号処理の本を読むと代表的なノイズ除去手法としてウィーナーフィルターが出てくるので、気になって実装してみました。
ウィーナーフィルターとは
ウィーナーフィルターは以下の評価関数\(\ J_{l}[k]\ \)を最小化するフィルタ \(G_{l}[k]\) のことです。
$$
J_{l}[k] = E[|S_{l}[k]-G_{l}[k]X_{l}[k]|^2]
$$
ここで、\(E[\cdot]\) は期待値、\(l\ \)はフレーム番号、\(k\ \)は周波数ビン番号です。
また、\(X_{l}[k]\ \)はSTFT後の観測信号であり、以下のようにSTFT後の音源信号\(\ S_{l}[k]\ \)とSTFT後のノイズ信号\(\ D_{l}[k]\ \)の和で表せます。
$$
X_{l}[k] = S_{l}[k] + D_{l}[k]
$$
上記の評価関数\(\ J_{l}[k]\ \)を最小化する\(\ G_{l}[k]\) について導出していきます。
ウィーナーフィルターの導出
さきほど\(\ G_{l}[k]\) を導出するといいましたが、参考文献[1] に導出方法が載っているので、ここでは割愛したいと思います。
結果的にはウィーナーフィルターは以下のようになります。
$$
\begin{align}
G^{\rm (WF)}_{l}[k] &= \frac{\sigma_s^2[l,k]}{\sigma_s^2[l,k] + \sigma_d^2[l,k]} \\[5pt]
&= \frac{\xi_{l}[k]}{1+\xi_{l}[k]}
\end{align}
$$
ここで、
$$
\begin{align}
\sigma_s^2[l,k] &= E[|S_l[k]|^2] \\[5pt]
\sigma_d^2[l,k] &= E[|D_l[k]|^2] \\[5pt]
\xi_{l}[k]&=\frac{\sigma_s[l,k]}{\sigma_d[l,k]}
\end{align}
$$
であり、\(\ \xi_{l}[k]\ \)は 事前SNRと呼ばれます。
ここまででウィーナーフィルターの導出はできましたが、事前SNR がわからないため、なんらかの推定法が必要となります。
事前SNRの推定
本記事では、参考文献[1]に掲載されている事前SNRの推定法を紹介します。
ノイズ信号の分散\(\ \sigma_d^2\ \)の推定
ノイズ信号の分散については、初期のフレームには音源信号がないとして、初期の\(\ Q\ \)フレームから\(\ \sigma_d^2\ \)を以下のように周波数ビンごとに推定していきます。
$$
\hat{\sigma}_{d}^2[l,k] = \frac{1}{Q}\sum_{l=0}^{Q-1} |X_l[k]|^2
$$
フレームごとにノイズ信号の分散は変化しないとします。
事前SNRの推定
音源信号については時々刻々と変化するため、事前SNR \(\ \xi_{l}[k]\ \)についてはフレーム番号、周波数ビン番号ごとに推定しなければなりません。
ここでは、判定指向法を使用して事前SNRを推定していきます。
判定指向法では、以下のように事前SNRを計算します。
\hat{\xi}_{l}[k] =
\left\{
\begin{array}{ll}
\beta \cfrac{|\hat{S}_{l-1}[k]|^2}{\sigma_d^2[k]}+(1-\beta)(\gamma_{l}[k]-1), & \gamma_l[k]>1 \tag{*} \\
\beta \cfrac{|\hat{S}_{l-1}[k]|^2}{\sigma_d^2[k]}, & {\rm otherwise}
\end{array}
\right.
$$
ここで、\(\beta\ \)は1以下の重み係数であり、\(\beta=0.98\ \)がよく利用されているそうです。また、\(\gamma_{l}[k]\)は事後SNR と呼ばれ、次式で与えられます。
$$
\gamma_{l}[k] = \frac{|X_{l}[k]|^2}{\sigma_{d}^2[l,k]}
$$
(*)式の\(\ \gamma_{l}[k]>1\ \)の場合については、
$$
\begin{align}
&\ \beta \cfrac{|\hat{S}_{l-1}[k]|^2}{\sigma_d^2[k]}+(1-\beta)(\gamma_{l}[k]-1) \\[5pt]
&= \beta \cfrac{|\hat{S}_{l-1}[k]|^2}{\sigma_d^2[k]}+(1-\beta)\cfrac{|X_{l}[k]|^2-\sigma_{d}^2[l,k]}{\sigma_{d}^2[l,k]} \\[5pt]
&\approx \beta \cfrac{|\hat{S}_{l-1}[k]|^2}{\sigma_d^2[k]}+(1-\beta)\cfrac{|S_{l}[k]|^2}{\sigma_{d}^2[l,k]}
\end{align}
$$
のように近似できるため、現在と過去のSNRの重み付き和として推定しているということです。
(*)式の\(\ \gamma_{l}[k]\leq 1\ \)の場合については、現在のSNRはゼロとして考えます。
プログラム
ソースコード
ウィーナーフィルターによるノイズ除去を行うソースコード wiener_filter.py は以下です。
import soundfile as sf
import numpy as np
import scipy.signal as sg
# パラメータ
Q_ms = 300 # ノイズ信号の分散を計算する区間 [ms]
N = 512 # 窓の大きさ
hop = N//2 # フレームシフトサイズ
window = "hann" # 窓の種類
beta = 0.98 # 事前SNR計算時の重み係数
wav_in_name = "input.wav" # 入力WAVファイル名
wav_out_name = "output.wav" # 出力WAVファイル名
# WAVファイルを読み込む
x, fs = sf.read( wav_in_name )
# 窓関数の作成
w_func = sg.get_window( window, N )
# 短時間フーリエ変換(STFT)
SFT = sg.ShortTimeFFT( win=w_func, hop=hop, fs=fs )
X_stft = SFT.stft(x)
# 必要な変数を用意
bin_num = X_stft.shape[0] # 周波数ビンの数
frame_num = X_stft.shape[1] # フレーム番号の数
# 音源信号(STFT) 初期化
S_stft = np.zeros( ( bin_num, frame_num ), dtype=complex )
# 1フレーム前の音源信号のパワー(STFT) 初期化
S_pow_pre = np.zeros( ( bin_num, 1 ) )
# 事前SNR 初期化
snr_pre = np.zeros( ( bin_num, frame_num ) )
# パワースペクトルを求める
X_power = np.abs( X_stft )
X_power = X_power**2
# ノイズ信号の分散を求める
## 計算区間を [ms]→[frame] に変換
Q = ((fs * 0.001 * Q_ms - N) // hop) + 1
Q = int(Q) # 整数に変換
## 周波数ごとの分散 var_d を求める
var_d = np.mean( X_power[:,:Q], axis=1 )
var_d = var_d.reshape( bin_num, 1 )
# 事後SNRを計算
snr_post = ( X_power / var_d )
# 前もって事前SNRの一部を計算
snr_pre = ( 1 - beta ) * ( snr_post - 1 )
tmp = ( snr_pre > 0 )
snr_pre = snr_pre * tmp # 事後SNRが1以下の場合はゼロとする
# フレームごとにウィーナーフィルターで音源信号を推定
for l in range( frame_num ):
## フレームごとに事前SNRを計算
snr_pre[:,l] += beta * ( S_pow_pre[:,0] / var_d[:,0] )
## フレームごとにウィーナーフィルターを計算
G_WF = snr_pre[:,l] / ( 1 + snr_pre[:,l] )
## フレームごとにウィーナーフィルターを乗算
S_stft[:,l] = G_WF * X_stft[:,l]
## 過去の音源信号パワーの更新
S_pow_pre[:,0] = np.abs( S_stft[:,l] )**2
# 逆短時間フーリエ変換
s = SFT.istft( S_stft, k1=x.shape[0] )
# WAVファイルを書き込む
sf.write( wav_out_name, s, fs, subtype='PCM_16' )
42~44行目:ノイズ信号の分散の計算区間を ms で与えているため、フレーム数に変換しています。
53~56行目:事前SNRの下図の四角に囲んだ箇所を計算しています。

73~74行目:観測信号 x と推定した音源信号 s の長さを揃えるために、k1 に x の長さを与えています。
実行方法
(1) プログラムを実行するディレクトリにソースコード(wiener_filter.py)とノイズを含む入力 WAV データを格納する。
(2) ソースコード5~12行目の入力データ名とパラメータを修正する。
# パラメータ
Q_ms = 300 # ノイズ信号の分散を計算する区間 [ms]
N = 512 # 窓の大きさ
hop = N//2 # フレームシフトサイズ
window = "hann" # 窓の種類
beta = 0.98 # 事前SNR計算時の重み係数
wav_in_name = "input.wav" # 入力WAVファイル名
wav_out_name = "output.wav" # 出力WAVファイル名
(3) 以下のコマンドで python を実行することで、 ノイズ除去したデータが出力される。
$ python wiener_filter.pyウィーナーフィルターの実行結果
ノイズを付加した音声データに対してウィーナーフィルターによるノイズ除去を適用してみました。
ノイズ除去した結果は以下となります。
入力音声(ノイズ含む)
出力音声(ノイズ除去後)
また、スペクトログラムを比較した結果は以下となります。
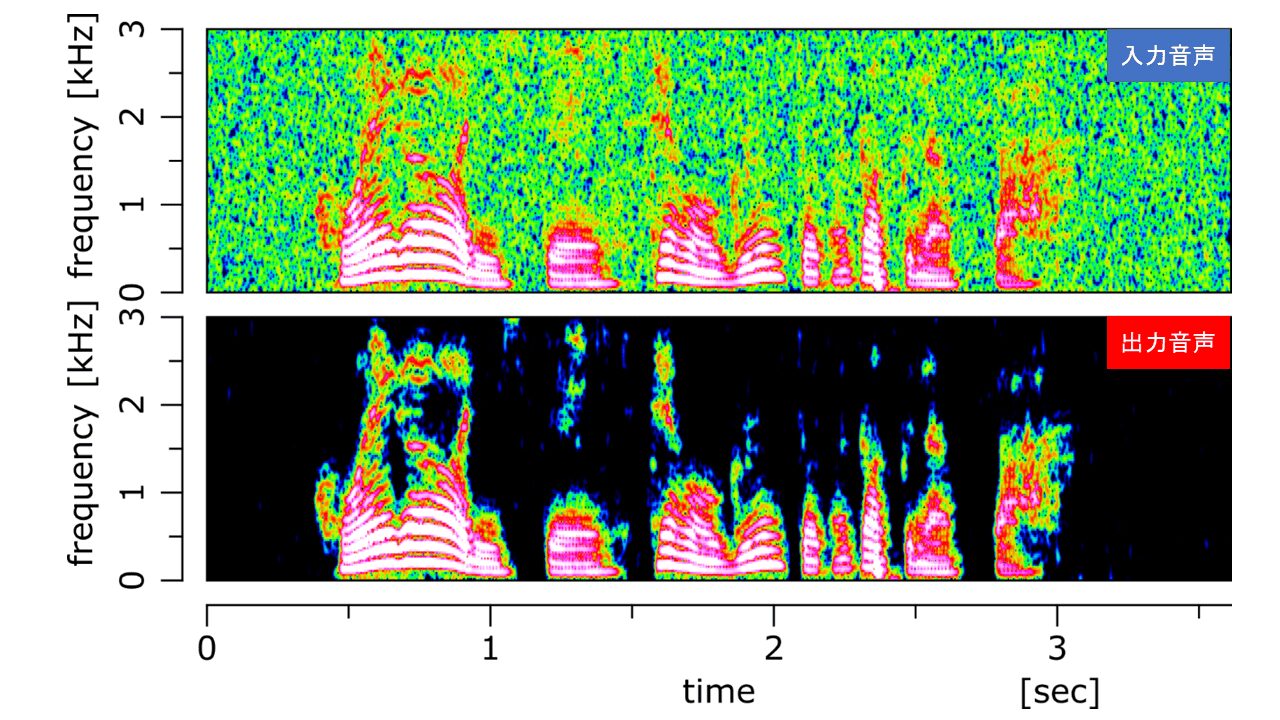
おわりに
今回はウィーナーフィルターによるノイズ除去を試してみました。
比較的単純なアルゴリズムでしたが、音声の品質を維持したままノイズ除去ができたのはすごかったです。また、複数の信号を必要とせず、一つの音声信号でノイズ除去が可能なのも良い点かなと思います。
ソースコード以外の説明につきましては、ほとんど参考文献をなぞっただけでしたので、詳細を知りたい方は参考文献をご覧になってください。
■参考文献
[1] 川村新、”音声音響信号処理の基礎と実践”、コロナ社、2021.
■使用した音声について
この記事で使用した音声は Mozilla Foundation で提供されている音声を使用させていただきました。
【音声のページ】
・ "Common Voice: A Massively-Multilingual Speech Corpus" 2020 Mozilla Foundation (Licensed under CC-0) https://huggingface.co/datasets/mozilla-foundation/common_voice_14_0
■変更履歴
・2025/04/13:数式の修正

