音の高さ(ピッチ)を揺らすビブラートを実装しました。
ビブラートとは周期的なピッチの揺れを付加するエフェクターとなります。
ビブラートについて
演奏や歌唱においてビブラートは音を伸ばしたとき、その音の高さを揺らすことをいいます。
とある女性歌手のロングトーンのスペクトログラムを以下に示します。
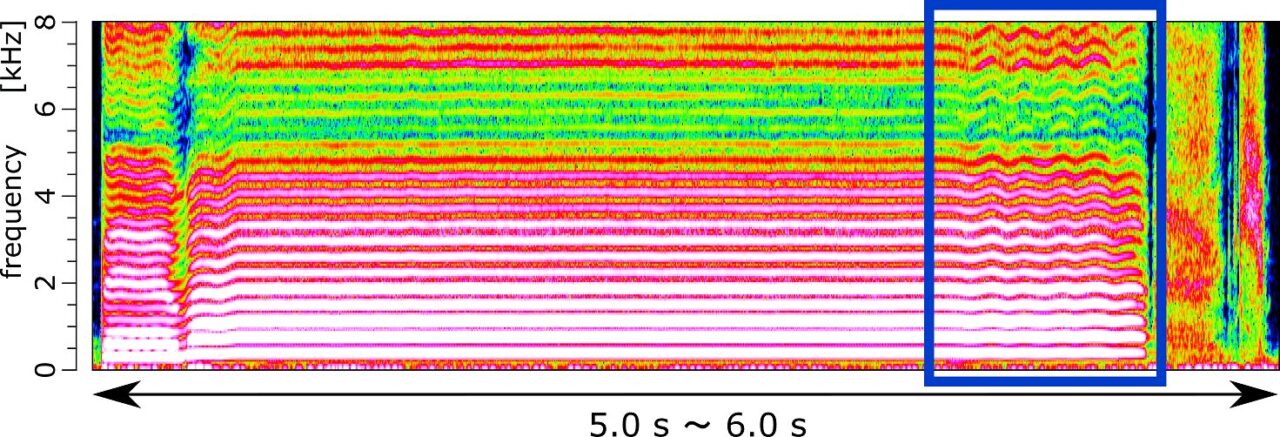
上図の青い四角で囲った部分がビブラートの箇所です。音の高さが上下に揺れているのがわかると思います。
この効果を人工的に付加するビブラートのエフェクターを実装していきます。
実装方法
いきなりビブラートの実装方法について説明します。
ビブラートは以下のように時間変動する遅延を与えることで実装できます。
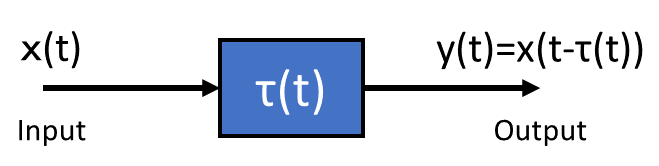
遅延は以下のようにします。
$$
\tau(t) = d+depth\cdot \sin(2\pi r t) \tag{*}
$$
ここで、depth はビブラートの深さ(DEPTH)、r はビブラートの周波数(RATE)を表す。d は平均遅延時間です。
デジタル処理する場合は、遅延を以下のようにすればよいです。
$$
\tau[n] = F_s \left(d + depth\cdot \sin\left(2\pi r \frac{n}{F_s}\right)\right)
$$
原理
参考文献[1][2] には上記のような実装方法が記載されておりますが、その原理については説明があまりないです。
一応、原理は「FM変調」や「ドップラー効果」と同じようなものと説明がありますが、いまいちピンとこないです。
今回、なぜ上記のような方法でビブラートが実装できるのか説明しようと思います。筆者独自の説明となりますので間違いがある可能性をご承知おきください。
遅延した正弦波の周波数
ビブラートを実装するには以下の周波数 f の正弦波を周波数が周期的に変動するように遅延時間 τ を決めればよいです。
$$
\sin(2\pi f (t-\tau(t))) \tag{A}
$$
角周波数は位相の微分のため、(A)式の角周波数は以下のように表せます。
$$
\omega = \frac{d\theta}{dt} = 2\pi f - 2\pi f \tau'(t) \tag{B}
$$
周波数は角周波数を2πで割ったものですので、(A)式の周波数は以下のように表せます。
$$
\frac{\omega}{2\pi} = f - f \tau'(t) \tag{C}
$$
遅延時間の求め方
ビブラートは(C)式の周波数を f を中心とした正弦波のように変動させたいため、(D)式が成り立つように遅延時間 τ を決定します。
$$
f - a \cos(2\pi r t) = f - f \tau'(t) \tag{D}
$$
ここで、a は周波数の最大変動量、r はビブラートの周波数です。
(D)式について:\(-a\cos(2\pi r t)\ \)より\(+a\sin(2\pi r t)\ \)のほうが正弦波としてわかりやすいと思いますが、(*)式を導くために天下り的にこうしています。
(D)式を整理すると以下です。
$$
\tau'(t) = \frac{a}{f} \cos{(2\pi rt)} \tag{E}
$$
(E)式を積分すると以下のように遅延時間 τ が求まります。
$$
\tau(t) = \frac{a}{2\pi rf} \sin{(2\pi rt)} + C \tag{F}
$$
Cは積分定数です。
(F)式で以下のように置き換えれば、(*)式の遅延時間と同じになります。
$$
\begin{align}
depth &= \frac{a}{2\pi r f} \tag{G} \\[5pt]
d &= C \tag{H}
\end{align}
$$
したがって、(*)式の遅延時間を使えば、ビブラートができるということです。
パラメータ depth の決め方:周波数 f=1kHz に対して最大変動量 a=60Hz、r=5Hz としたい場合、depth=0.019s に設定すればよいです。
パラメータ d の決め方:(F)式を満たしていれば、ビブラートは実現できるので、パラメータ d は何でもよいですが、リアルタイム処理の場合、遅延時間 τ が負であるとレイテンシが多くなるため、d≧depth とします。
プログラム
ビブラートのエフェクトをかけるプログラムをPythonで実装しました。ソースコードと実行方法について説明します。
ソースコード
ビブラートのソースコード vibrato.py は以下です。
import soundfile as sf
import numpy as np
import math
# パラメータ
d = 0.002 # 平均遅延時間 [s]
r = 5 # ビブラートの周波数 [Hz]
depth = 0.002 # ビブラートの深さ [s]
wav_in_name = "input.wav" # 入力WAVデータ名
wav_out_name = "output_a.wav" # 出力WAVデータ名
# WAVファイルを読み込む
x, fs = sf.read(wav_in_name)
# 必要な値を設定
length_x = x.shape[0] # 入力信号の長さ
y = np.zeros(length_x) # 出力信号
d = d * fs # [s]->[sample]
depth = depth * fs # [s]->[sample]
# 繰り返し処理
for n in range(length_x):
tau = d + depth * math.sin(2*math.pi*r*n/fs) # 遅延時間
t = n - tau
# 線形補間
m = int(t)
if m+1 >= length_x: # 入力信号がなければ
break # 繰り返し処理を終了.
delta = t - m
y[n] = delta * x[m+1] + (1.0 - delta) * x[m]
if np.max(np.abs(y)) > 1.0:
y = y/np.max(np.abs(y)) # ノーマライズ
sf.write(wav_out_name, y, fs, subtype='PCM_16')23行目:(*)式の遅延時間 τ を設定する。
26~31行目:(*)式の遅延時間は整数とは限らず、サンプルとサンプルの中間値を求める必要がある。ここでは、以下のように線形補間によってその中間値を求める。
$$
\begin{align}
y[n] &= \delta \cdot x[m] + (1-\delta) \cdot x[m+1] \\[4pt]
t &= n-\tau \\[4pt]
\delta &= t-m
\end{align}
$$
\(m\ \) は\(\ m\leq t < m+1\ \)という関係を満足する整数です。
33~34行目:オーバーフローしたとき、ノーマライズする。
実行方法
(1) プログラムを実行するディレクトリにソースコード(vibrato.py)と入力 WAV データを格納する。
(2) ソースコード5~10行目のパラメータと入出力データ名を修正する。
# パラメータ
d = 0.002 # 平均遅延時間 [s]
r = 5 # ビブラートの周波数 [Hz]
depth = 0.002 # ビブラートの深さ [s]
wav_in_name = "input.wav" # 入力WAVデータ名
wav_out_name = "output_a.wav" # 出力WAVデータ名
(3) 以下のコマンドで python を実行することで、ビブラートのエフェクトをかけたWAVデータが出力される。
$ python vibrato.py処理結果
以下のようにパラメータを設定して、ビアノのラの音にビブラートのエフェクトをかけました。
| パラメータ名 | 変数名 | 設定値 |
|---|---|---|
| 平均遅延時間 | d | 0.002 [s] |
| ビブラートの周波数(RATE) | r | 5 [Hz] |
| ビブラートの深さ(DEPTH) | depth | 0.002 [s] |
ビブラートのエフェクトをかけたピアノ音は以下のようになります。
入力データ
ビブラート後のデータ
すごい音がビヨンビヨンしてますね。
スペクトログラムを以下に示します。
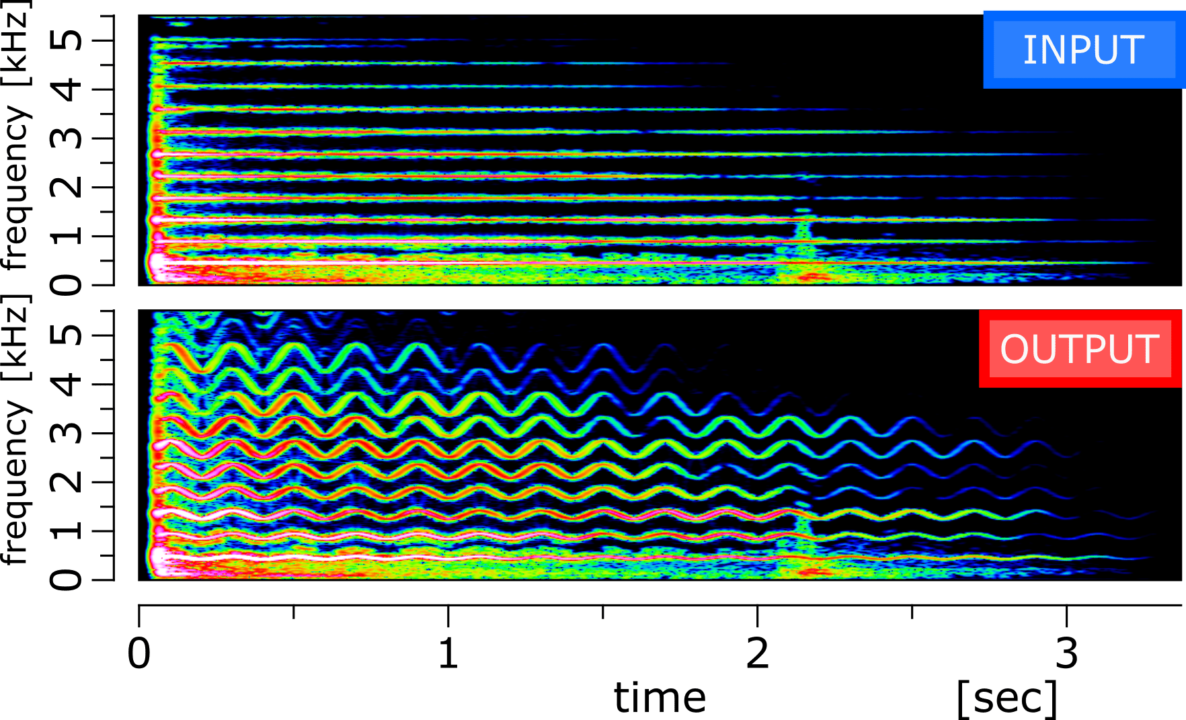
スペクトログラムからピッチが揺れており、ビブラートの効果を確認できると思います。
おわりに
本記事では、ビブラートを実装してみました。遅延時間を調整すればピッチの変動を三角波や矩形波のようにすることもできそうですね。時間があれば試してみます。
■参考文献
[1] 青木直史、”C言語ではじめる音のプログラミング”、オーム社、2008.
[2] 川村新、”プログラム101付き音声信号処理”、CQ社、2021.
■使用した楽器音データについて
この記事で使用したデータは 魔王魂 で提供されている楽器音データを使用させていただきました。
・ "ピアノ2-6ラ" © 2010 森田交一 (Licensed under CC BY 4.0) https://maou.audio/se_inst_piano2_6ra/
■変更履歴
・2025/01/30:タグの削除
