本記事ではRemez法によるFIRフィルタ設計について紹介します。
前回の記事(窓関数法によるFIRフィルタ設計)で窓関数法を紹介しましたが、Remez法については窓関数法よりも実用的なFIRフィルタ設計法となります。
Remez法の概要
Remez 法は1934年に Evgeny Yakovlevich Remez によって発表された近似関数を求める反復アルゴリズムです[1]。1972年に McClellan と Parks が Remez 法を FIR フィルタの設計に適用したため、FIRフィルタの設計では McClellan-Parks 法とも呼ばれます。
Remez法の特徴としては下図のようにフィルタのリプルの大きさが周波数全体で等しい特性(等リプル特性)を持つことです。
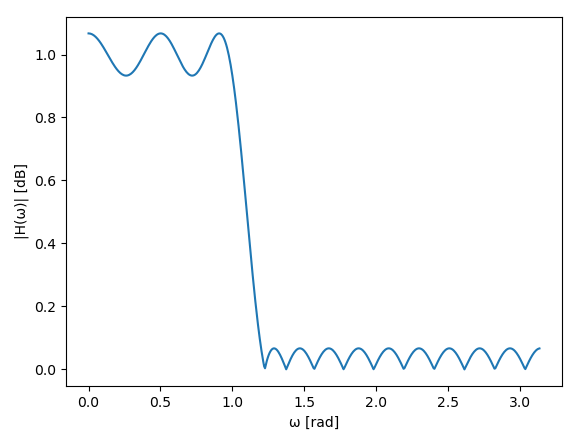
パラメータ(フィルタの次数や遷移域の幅)の指定によっては繰り返し計算で収束せず、フィルタを作成できないことがありますが、作成できれば他の設計法より良好なフィルタが作成できます。
Remez法の詳細
線形位相FIRフィルタ
Remez法では以下のようにフィルタ次数\(N\)が偶数(タップ長(\(N+1\))は奇数)、偶対称のインパルス応答をもつ線形位相FIRフィルタを設計対象とします。
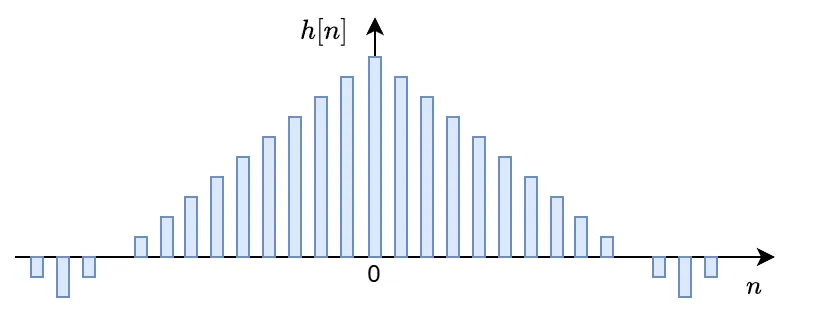
上図のような偶数次・偶対称のインパルス応答の場合、周波数特性は離散時間フーリエ変換(DTFT)によって以下のように求められます。
$$
\begin{align}
H(\omega) &= \sum_{n=-\infty}^{\infty} h[n]e^{-jn\omega} \\[5pt]
&= h[0] + \sum_{n=1}^{N/2} 2h[n] \frac{e^{jn\omega}+e^{-jn\omega}}{2} \\[5pt]
&= h[0] + \sum_{n=1}^{N/2} 2h[n] \cos{(n\omega)} \tag{1}
\end{align}
$$
n=0 を中心とした偶数次・偶対称インパルス応答の周波数特性は実数となるため、取り扱いが楽になっています。
因果性を満たしたフィルタを作成したい場合は、設計したインパルス応答を N/2 だけ右にシフトすればよいです。
後の計算でわかりやすいように(1)式は以下のように表しておきます。
$$
H(\omega) = \sum_{m=0}^{M} a_{m} \cos{(m\omega)} \tag{2}
$$
ここで、\(M=N/2\)、\(a_{0}=h[0]\ \)、\(a_{m}=2h[m](1\leq m \leq M)\ \)である。
ミニマックス問題
Remez法では通過域と阻止域において以下の誤差関数の絶対値\(\ |e(\omega)|\ \)の最大値が最小となる\(\ a_{m}\ \)を求めることで最適なフィルタを作成します。
\begin{align}
e(\omega) &= W(\omega) (H(\omega) - H_{ideal}(\omega)) \\[5pt] &= W(\omega) \left(\sum_{m=0}^{M} a_{m} \cos{(m\omega)} - H_{ideal}(\omega)\right) \tag{3}
\end{align}
$$
ここで、\(W(\omega)\ \)は重み関数、\(H_{ideal}(\omega)\) は以下のような所望周波数特性です。
H_{ideal}(\omega) =
\begin{cases}
1 & 0 \leq \omega \leq \omega_{p} \\[5pt] don't\ care & \omega_{p} \leq \omega \leq \omega_{s} \tag{4} \\[5pt] 0 & \omega_{s} \leq \omega \leq \pi
\end{cases}
$$
\(\omega_{p}\) は通過域端角周波数、\(\omega_{s}\) は阻止域端角周波数です。
重み関数については、作成されるフィルタの通過域と阻止域のリプルの大きさの比率を変えるために使用します。例えば、阻止域のリプル\(\ \delta_{s}\ \)を通過域のリプル\(\ \delta_{p}\ \)よりも1/2小さくしたい場合は、阻止域の\(W(\omega)\)を通過域の2倍にすればよいです。
交番定理
ミニマックス問題においては交番定理(alternation thorem)が成立することがわかっています。
交番定理とは\(\ H(\omega)\ \)が最良近似となる必要十分条件は以下であるという定理です[3]。
- 近似帯域上で近似誤差\(\ e(\omega)\ \)の符号が少なくとも\(\ M+1\ \)回変わる
- \(e(\omega)\ \)の極値の符号が正負を繰り返す(交番する)
- \(e(\omega)\ \)の極値の絶対値がすべて等しい
つまり、最良近似となる\(\ H(\omega)\ \)は以下の図のようになるということです。
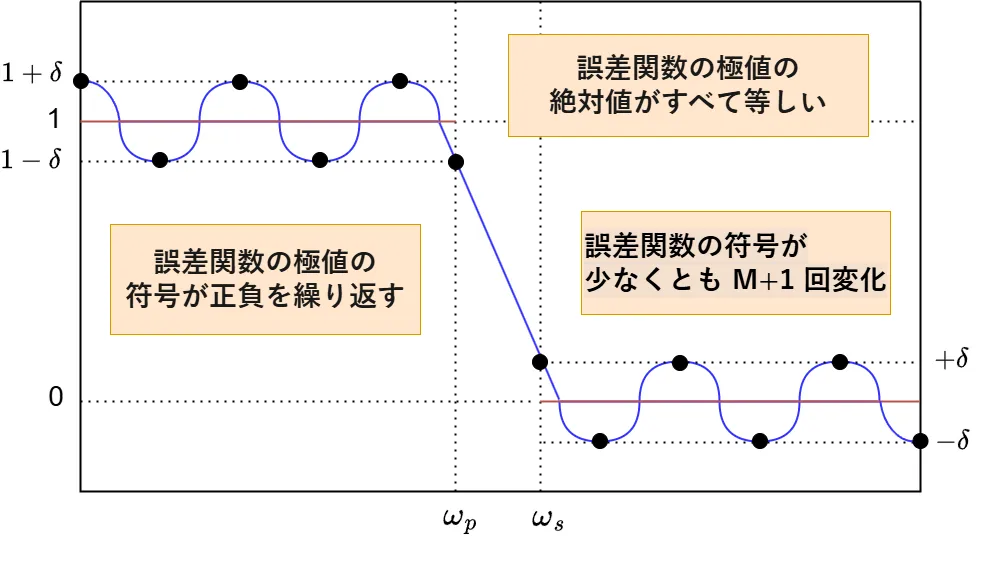
Remez法では交番定理を用いて、最良近似となる\(\ H(\omega)\ \)を繰り返し計算で求めていきます。
Remez法の流れ
Remez法の大まかな流れとしては以下となります。
1. 誤差関数の極値となりうる点 \(\ \omega_i\ \)を M+2 個設定する。
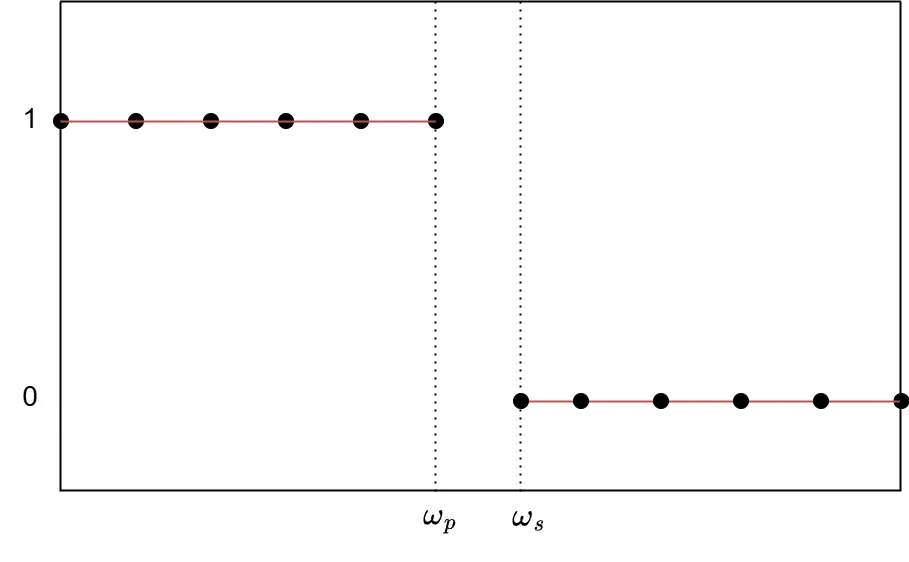
通過域と阻止域に誤差関数の極値点 M+2 個を設定します。上図は M=10 の場合です。
2. \(\omega_i\ \)における誤差が正負を繰り返し、誤差の大きさが等しくなる\(\ H(ω)\ \)を求める。
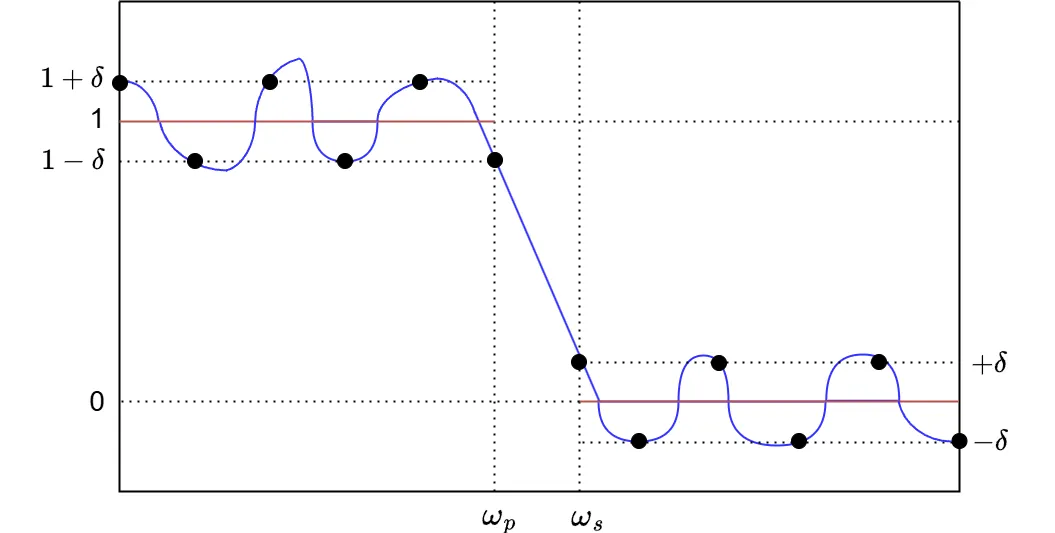
設定した\(\ \omega_i\ \)での誤差が正負を繰り返し、\(\omega_{i}\ \)の誤差の大きさが等しくなる上図のような\(\ H(ω)\ \)を求めます。これで、交番定理の「\(e(ω)\ \)の極値の絶対値がすべて等しい」という条件以外は満たされます。
3. 収束してなければ求めた\(\ H(ω)\ \)の極値の点を\(\ \omega_i\ \)に設定して②に戻る。
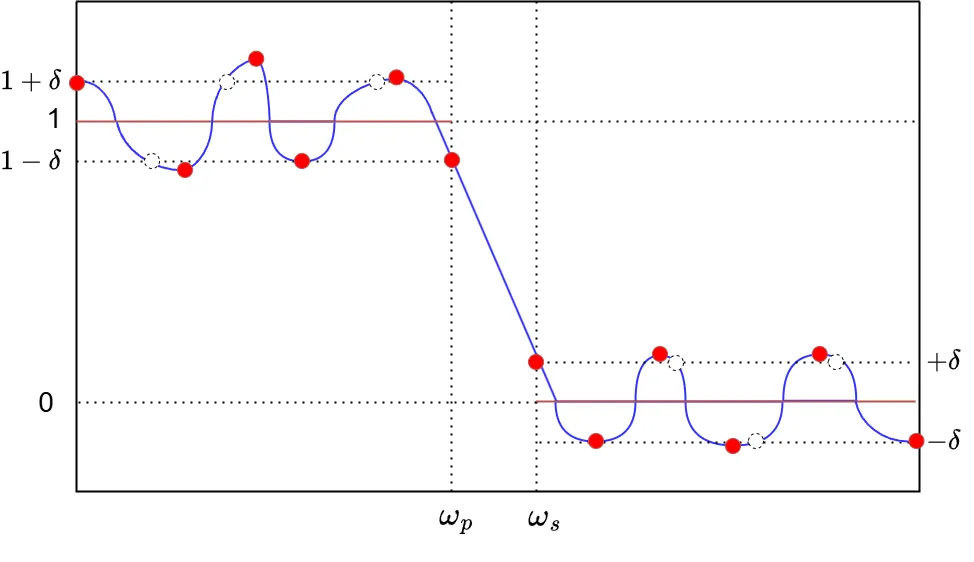
\(\omega_{i}\ \)を\(\ e(\omega)\ \)の新たな極値点に再設定して、繰り返し計算で \(H(\omega)\) を最良近似に近づけていきます。イメージとしては盛り上がった金属板を叩いて平らにする感じです。
②で求めた\(\ H(\omega)\ \)の極値点が M+2 個も存在しない場合、最初の初期設定からやり直しとなります。
FIRフィルタ設計手順
Remez法によるFIRフィルタ設計手順[4]は以下です。
- 極値点となりうる角周波数 \(\omega_{i}^{(0)}\ \)を M+2 個設定する。
- \(\omega_{i}^{(k)}\ \)における誤差が正負を繰り返し、誤差の大きさが等しくなる\(\ H(\omega)^{(k)}\ \) を連立方程式\({\ \boldsymbol A}{\boldsymbol x}={\boldsymbol b}\ \)を解くことで求める。
- \(e(\omega)\ \)の極値点 \(\omega_{i}^{(k+1)}\)を探索して求め、\(\max_{i}|\omega_{i}^{(k+1)}-\omega_{i}^{(k)}|<\epsilon\) ならば終了、そうでなければ\(k\leftarrow k+1\)として、②へ戻る。
極値点の初期設定
極値点の初期設定は任意性がありますが、以下の4点だけは必ず極値点となります。
$$
\omega = 0,\ \omega_{p},\ \omega_{s},\ \pi \tag{5}
$$
フィルタの振幅特性は\(\ \omega=0,\pi\ \) において線対称であるため、\(\ 0,\pi\ \)で必ず極値点となります。
さらに、\(\omega_{p}\ \)では振幅特性が阻止域に向かって下がるため、誤差関数が負のピーク値となり、逆に\(\ \omega_{s}\ \)では誤差関数が正のピーク値となります(厳密には端点は極値点とはならないですが、説明の都合上、この記事では極値点とする)。
残りの極値点については近似帯域上を等分割して配置すればよいことが経験的に知られています。そのため、通過域には
$$
M_{p} = \left\lceil(M+2)\times \frac{\omega_{p}}{\omega_{p}+(\pi-\omega_{s})}\right\rceil \tag{6}
$$
の極値点を等分割に配置します。残りの極値点については阻止域に等分割に配置します。
フィルタ係数\(\ a_{m}\ \)の求め方
\(H(\omega)^{(k)}\ \)については以下の連立方程式を解くことで求めます。
W(\omega_{i})\left(\sum_{m=0}^{M} a_{m} \cos{(m\omega_{i})} -H_{ideal}(\omega_{i}) \right) = (-1)^{i}\delta \tag{7}
$$
ここで、\(\delta\ \) は\(\ \omega_{i}\ \)における誤差の大きさ(マイナスも可)です。未知数が M+2 個のため上記の連立方程式は解くことができます。
(7)式の連立方程式の解き方としては以下のように行列で表記を行い、
$$
{\boldsymbol A}{\boldsymbol x}={\boldsymbol b} \tag{8}
$$
\begin{align}
{\boldsymbol A} &=
\begin{bmatrix}
1 & \cos{(\omega_{0})} & \cdots & \cos{(M\omega_{0})} & (-1)^{0}/W(\omega_{0}) \\
\vdots & \vdots & \ddots & \vdots & \vdots \\
1 & \cos{(\omega_{M})} & \cdots & \cos{(M\omega_{M})} & (-1)^{M}/W(\omega_{M}) \\
1 & \cos{(\omega_{M+1})} & \cdots & \cos{(M\omega_{M+1})} & (-1)^{M+1}/W(\omega_{M+1}) \\
\end{bmatrix} \\[5pt] {\boldsymbol x} &=
\begin{bmatrix}
a_{0} & a_{1} & \cdots & a_{M} & \delta
\end{bmatrix}^T \\[5pt] {\boldsymbol b} &=
\begin{bmatrix}
H_{ideal}(\omega_{0}) & H_{ideal}(\omega_{1}) & \cdots & H_{ideal}(\omega_{M}) & H_{ideal}(\omega_{M+1})
\end{bmatrix}^T
\end{align}
$$
\({\boldsymbol A}\ \)の逆行列を左から掛けることで、\({\boldsymbol x}\ \)を求めることができます。
$$
{\boldsymbol x}={\boldsymbol A}^{-1}{\boldsymbol b} \tag{9}
$$
極値点の探索
極値点の探索については、通過域\(\ [0,\omega_{p}]\ \)と阻止域\(\ [\omega_{s},\pi]\ \) において、(10)式と(11)式が成り立つ\(\ l\pi/L\ \)(\(1\leq l\ \leq L-1\))を極値点\(\ \omega_{i}^{(k+1)}\ \)とします。
$$
\begin{align}
\left|H\left(\frac{(l-1)\pi}{L}\right)\right| < \left|H\left(\frac{l\pi}{L}\right)\right| \tag{10} \\[5pt]
\left|H\left(\frac{(l+1)\pi}{L}\right)\right| < \left|H\left(\frac{l\pi}{L}\right)\right| \tag{11}
\end{align}
$$
極値点の最大の変化量が収束判定定数\(\ \epsilon\ \)よりも小さければ、繰り返し計算を終了とします。
$$
\max_{i}|\omega_{i}^{(k+1)}-\omega_{i}^{(k)}|<\epsilon \tag{12}
$$
収束していなければ、\(k\leftarrow k+1\) として、\(H(\omega)^{(k)}\)を繰り返し求めます。
終了時は\(\ a_{m}\ \)から\(\ h[n]\ \)を求めておきます。
$$
\begin{align}
h[0] &= a_{0} \\[5pt]
h[m] &= \frac{a_{m}}{2} \hspace{1em}(m=1,\cdots,M) \tag{13} \\[5pt]
h[-m] &= \frac{a_{m}}{2} \hspace{1em}(m=1,\cdots,M)
\end{align}
$$
プログラム
Remez法でFIRフィルタを設計するプログラムをPythonで書いてみました。
ソースコード
Remez法を使用してFIRフィルタ係数を出力するソースコード remez.py は以下です。
import numpy as np
import scipy.signal as sg
import math
import matplotlib.pyplot as plt
import sys
# コマンドラインの引数を取得
args = sys.argv
if len(args)!=5:
print("\nusage: python remez.py omega_s omega_p M delta_p2s")
print(" omega_p : passband edge frequency")
print(" omega_s : stopband edge frequency")
print(" M : filter order / 2")
print(" delta_p2s : Magnitude of the ripple of the passband to the stopband")
raise Exception("Argument error ")
# パラメータ
omega_p = float(args[1]) # 通過域端角周波数
omega_s = float(args[2]) # 阻止域端角周波数
M = int(args[3]) # フィルタ次数/2
delta_p2s = float(args[4]) # 阻止域に対する通過域のリプルの大きさ
L = 100000 # [0,π] の分割数
K = 1000 # 最大繰り返し回数
epsilon = (2*np.pi)/L # 収束判定定数
def Calculate_x(omega_arr, A_arr, b_arr):
"""
ベクトルx (フィルタ係数a と 誤差δ)を計算
Parameters
----------
omega_arr (np.array) : 極値点 ωi
A_arr (np.array) : 行列 A
b_arr (np.array) : ベクトル b
Returns
-------
x_arr (np.array) : ベクトル x
"""
# グローバル変数宣言
global M
# 行列A を計算
for m in range(M+1):
A_arr[:,m] = np.cos(m*omega_arr)
A_inv_arr = np.linalg.pinv(A_arr)
x_arr = np.matmul(A_inv_arr, b_arr)
return x_arr
def search_error_peak(omega_start, omega_end, a_arr, search_pt_num, passband_flg):
"""
H(ω)の極値点を探索して、極値点を返す
Parameters
----------
omega_start (float) : 探索開始点 [rad]
omega_end (float) : 探索終了点 [rad]
a_arr (np.array) : フィルタ係数
search_pt_num (int) : 探索点数
passband_flg (bool) : 1:通過域の探索 0:阻止域の探索
Returns
-------
omega_arr (np.array) : 極値点
"""
# グローバル変数宣言
global L
global M
# 変数宣言
## 極値点の初期化
omega_arr = np.zeros(search_pt_num)
omega_arr[0] = omega_start
omega_arr[search_pt_num-1] = omega_end
## 探索開始点と終了点
start_pt = math.ceil((omega_start/np.pi) * L) + 1
end_pt = math.floor((omega_end/np.pi) * L) - 1
## 極値点のインデックス
m_arr = np.arange(M+1)
m = 1
# 探索
for l in range(start_pt,end_pt+1):
## H(lπ/L)を求める
omega_pre = ((l-1)*np.pi)/L
omega_tmp = (l*np.pi)/L
omega_next = ((l+1)*np.pi)/L
e_pre = np.abs(np.sum(a_arr * np.cos(m_arr*omega_pre) ) - passband_flg)
e_tmp = np.abs(np.sum(a_arr * np.cos(m_arr*omega_tmp) ) - passband_flg)
e_next = np.abs(np.sum(a_arr * np.cos(m_arr*omega_next)) - passband_flg)
## 極値点の判定
if e_tmp > e_pre and e_tmp > e_next:
omega_arr[m] = omega_tmp
m += 1
### 指定した数の極値点を見つけたら探索終了
if m == search_pt_num-1:
break
# 指定した数の極値点を見つけられなかったらエラー表示
if m != search_pt_num-1:
print("search_pt_num={}, m={}".format(search_pt_num, m) )
raise Exception("Search Failure in [{},{}]".format(omega_start, omega_end))
return omega_arr
# パラメータから計算
## M_p の計算
M_p = math.ceil((M+2)*(omega_p/(omega_p+(np.pi-omega_s))))
## x の初期化
x_arr = np.zeros((M+2, 1))
## b の初期化
b_arr = np.ones((M+2, 1))
b_arr[M_p:,0] = 0
## A の初期化
A_arr = np.ones((M+2,M+2))
for i in range(M_p):
A_arr[i,M+1] = (-1)**(i) * delta_p2s
for i in range(M_p,M+2):
A_arr[i,M+1] = (-1)**(i)
# (1) 極値点の初期設定
omega_arr = np.zeros(M+2)
omega_arr[0:M_p] = np.linspace(0, omega_p, M_p)
omega_arr[M_p:M+2] = np.linspace(omega_s, np.pi, M+2-M_p)
omega_old_arr = np.copy(omega_arr)
# (2)-(3) 繰り返し計算
for k in range(K):
# イタレーション番号表示
print("k={}".format(k))
## (2) フィルタ係数amの計算
x_arr = Calculate_x(omega_arr, A_arr, b_arr)
## (3) 極値点の探索
### [0,ωp] の探索
omega_start = 0
omega_end = omega_p
a_arr = x_arr[0:M+1,0]
search_pt_num = M_p
passband_flg = 1
omega_arr[0:M_p] = search_error_peak(omega_start, omega_end, a_arr, search_pt_num, passband_flg)
### [ωs,π] の探索
omega_start = omega_s
omega_end = np.pi
a_arr = x_arr[0:M+1,0]
search_pt_num = M+2-M_p
passband_flg = 0
omega_arr[M_p:M+2] = search_error_peak(omega_start, omega_end, a_arr, search_pt_num, passband_flg)
### 収束判定
omega_diff = omega_arr - omega_old_arr
if np.max(omega_diff) < epsilon:
break
else:
omega_old_arr = np.copy(omega_arr)
# 誤差
delta = x_arr[M+1,0]
# フィルタ係数
h_arr = np.zeros(2*M+1)
h_arr[0:M+1] = a_arr[::-1]/2
h_arr[M+1:2*M+1] = a_arr[1:]/2
h_arr[M] = a_arr[0]
# 周波数特性の計算
w, H = sg.freqz(h_arr)
H_dB = 20 * np.log10(np.abs(H))
# グラフ出力
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(w, H_dB, color="tab:blue")
ax.set_xlabel("ω [rad]")
ax.set_ylabel("|H(ω)| [dB]")
# インパルス応答と周波数特性を出力
print(h_arr)
print("delta={}".format(delta))
fig.savefig("ftoku.png")
7~15行目:コマンドの引数を取得する。引数が4つ(実行ファイル(.py)を入れると5つ)ないときはコマンドの使用方法を出力する。
17~24行目:コマンドから取得した引数を変数に格納する。また、残りのパラメータを設定する。
26~52行目:手順②のフィルタ係数を求める関数。
54~114行目:手順③の誤算関数の極値点の探索をする関数。
116~132行目:パラメータから計算できる変数をあらかじめ計算する。
134~138行目:手順①の極値点の初期設定を行う。
140~171行目:手順②と③の繰り返し計算を行う。収束していたら、イタレーションを抜ける。
173~196行目:フィルタ係数を求めて、フィルタの周波数特性をグラフに出力する。
実行方法
(1) プログラムを実行するディレクトリにソースコード(remez.py)を格納する。
(2) ソースコード17~24行目のパラメータ(L, k, epsilon)を修正する。
# パラメータ
omega_p = float(args[1]) # 通過域端角周波数
omega_s = float(args[2]) # 阻止域端角周波数
M = int(args[3]) # フィルタ次数/2
delta_p2s = float(args[4]) # 阻止域に対する通過域のリプルの大きさ
L = 100000 # [0,π] の分割数
K = 1000 # 最大繰り返し回数
epsilon = (2*np.pi)/L # 収束判定定数
(3) 以下のコマンドで python を実行する。
$ python remez.py 1.0 1.1 40 1コマンドの引数の意味は以下となります。
| 引数 | パラメータ名 | 記号 | 変数名 |
|---|---|---|---|
| 1 | 通過域端角周波数 | \(\omega_p\) | omega_p |
| 2 | 阻止域端角周波数 | \(\omega_s\) | omega_s |
| 3 | 次数/2 | \(M\) | M |
| 4 | 阻止域に対する通過域のリプルの大きさ | \(\delta_p/\delta_s\) | delta_p2s |
処理結果
パラメータを以下の表のように設定してFIRフィルタを作成しました。
| パラメータ名 | 記号 | 変数名 | 値 |
|---|---|---|---|
| 通過域端角周波数 | \(\omega_p\) | omega_p | 1.0 |
| 阻止域端角周波数 | \(\omega_s\) | omega_s | 1.5 |
| 次数/2 | \(M\) | M | 20 |
| 阻止域に対する通過域のリプルの大きさ | \(\delta_p/\delta_s\) | delta_p2s | 1.0 |
| [0,π] の分割数 | \(L\) | L | 100000 |
| 最大繰り返し回数 | \(K\) | K | 1000 |
| 収束判定定数 | \(\epsilon\) | epsilon | (2π)/L |
作成したRemez法によるFIRフィルタの周波数特性は以下です。比較として窓関数法で作成したFIRフィルタも載せています。
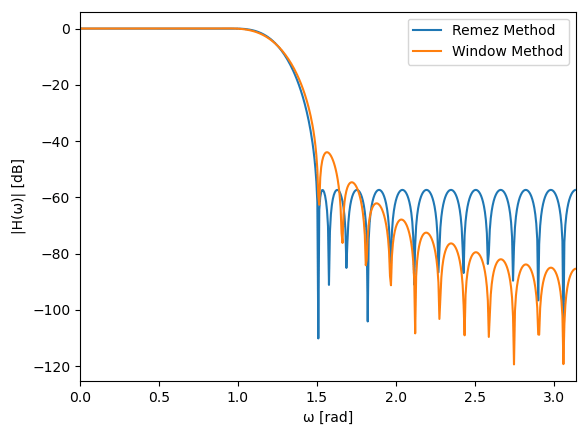
グラフからわかるようにRemez法で作成したフィルタは阻止域のリプルの大きさが等しくなります。一方、窓関数法で作成したフィルタは遷移域から離れるにつれてリプルの大きさが小さくなります。
\(1.7\ \leq \omega \leq \pi\ \) では窓関数法のフィルタのほうが周波数特性が良くなっていますが、\(1.5 \leq \omega \leq 1.7\ \) ではRemez法のフィルタのほうが周波数特性が良くなっています。一見すると窓関数法のほうが周波数特性が良く見えますが、阻止域の振幅特性の最大値はRemez法のほうが小さいため、実用的にはRemez法のほうが良い場合が多いです。
おわりに
本記事では、Remez法によるFIRフィルタ設計法を紹介いたしました。
繰り返し計算でFIRフィルタを作成するため、パラメータによっては安定したフィルタを作れないのが嫌な点ですが、遷移域のサイズを指定できるのは個人的に良い点です。
気になったフィルタ設計法を見つけたら、また紹介したいと思います。
参考文献
[1] Wikipedia, “Remezのアルゴリズム,” https://ja.wikipedia.org/wiki/Remezのアルゴリズム, (参照2025-01-21).
[2] 英語版 Wikipedia, “Parks–McClellan filter design algorithm,” https://en.wikipedia.org/wiki/Parks–McClellan_filter_design_algorithm, (参照2025-01-21).
[3] 谷荻隆嗣, ”ディジタルフィルタと信号処理,” コロナ社, pp149-165, 2001.
[4] 陶山健仁, ”ディジタルフィルタ原理と設計法,” 科学情報出版株式会社, pp.214-232, 2018.
■変更履歴
・2025/01/30:タグの変更
・2025/03/09:Remez法の概要の追加
