Pythonで打楽器音を合成してみた

今回は打楽器音の合成をしました。打楽器音の合成にはKarplus-Strong方式を使用しております。

合成方法

(1) 遅延数 \(\ p\ \) と確率 \(\ b\ \) を適当に決定。

(2) \(\ x_0 \cdots x_{p}\) に乱数（白色雑音）を入れる。\(x_n (n\geq p+1)\) には０を入れる。

(3) 以下の式によってデジタルフィルタをかける。

プログラム

Karplus Strong方式で打楽器音を合成するプログラムを作りました。

import sys
import scipy.signal as sg
import numpy as np
import soundfile as sf

# コマンドラインの引数を取得
args = sys.argv
if len(args)!=5:
    print("nusage: python Karplus.py amp filename p b")
    print("   amp        : amplitude")
    print("   filename   : file name of sound")
    print("   p          : Number of delays")
    print("   b          : Probability")
    raise Exception("Argument error ")

amp = float(args[1]) # 初期値の振幅範囲
filename = args[2]   # ファイル名
p = int(args[3])     # 遅延数
b = float(args[4])   # 確率

fs = 48000               # サンプリング周波数
interval = int(fs*0.5)   # 音符が変化する間隔
n_data = interval*7      # データの数
wave = np.zeros(n_data)  # 波形データを入れる場所 

for i in range(7):

    # 乱数生成
    n = i*interval
    wave[n:n+p+1] = (np.random.rand(p+1)-0.5)*amp
    rd = np.random.rand(interval)

    # デジタルフィルタに通す
    for m in range(interval):
        if m > p:
            wave[n+m] = 0.5*(wave[n+m-p]+wave[n+m-p-1])
            if rd[m] > b:
                wave[n+m] *= -1.0

sf.write(filename, wave, fs, subtype='PCM_16')

合成した打楽器音

サンプリング周波数 \(f_s=48{\rm kHz}\), \(p=400\), \(b=0.2, 0.5, 0.8\) で合成した打楽器音が以下です。

\(b=0.2\)

\(b=0.5\)

\(b=0.8\)

\(b\) が 0 や 1 に近いと、撥弦音と打楽器音が混ざったような音になりますね。

波形とスぺクトログラムの観察

合成した打楽器音の波形とスぺクトログラムは以下です。

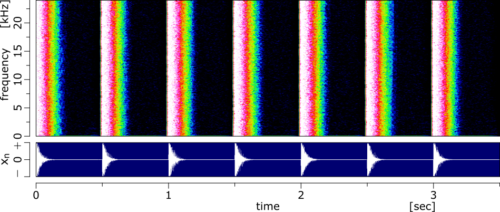
撥弦音の場合、ある特定の周波数成分だけがゆっくり減衰していたのに対して、打楽器音は全ての周波数成分がゆっくり減衰しています。\(p\) を長くすることで減衰時間が長くなるそうです。

おわりに

今回は打楽器音の合成を試してみました。打楽器だけで演奏しても何の曲を演奏しているかわからないと思いますので、他の楽器音と一緒に演奏しようと思います。

参考文献