管楽器のフルートの音を合成してみました。いままで撥弦音や打楽器音は合成していましたが、管楽器は試していなかったので気になって挑戦してみました。
また、参考文献[1] を半年前に購入してはいたのですが、ずっと読めずにいたので、これを機に主要な部分を読み進めようと思った次第です。
フルート音の解析
フルート音の波形とスペクトログラムを以下に示します。
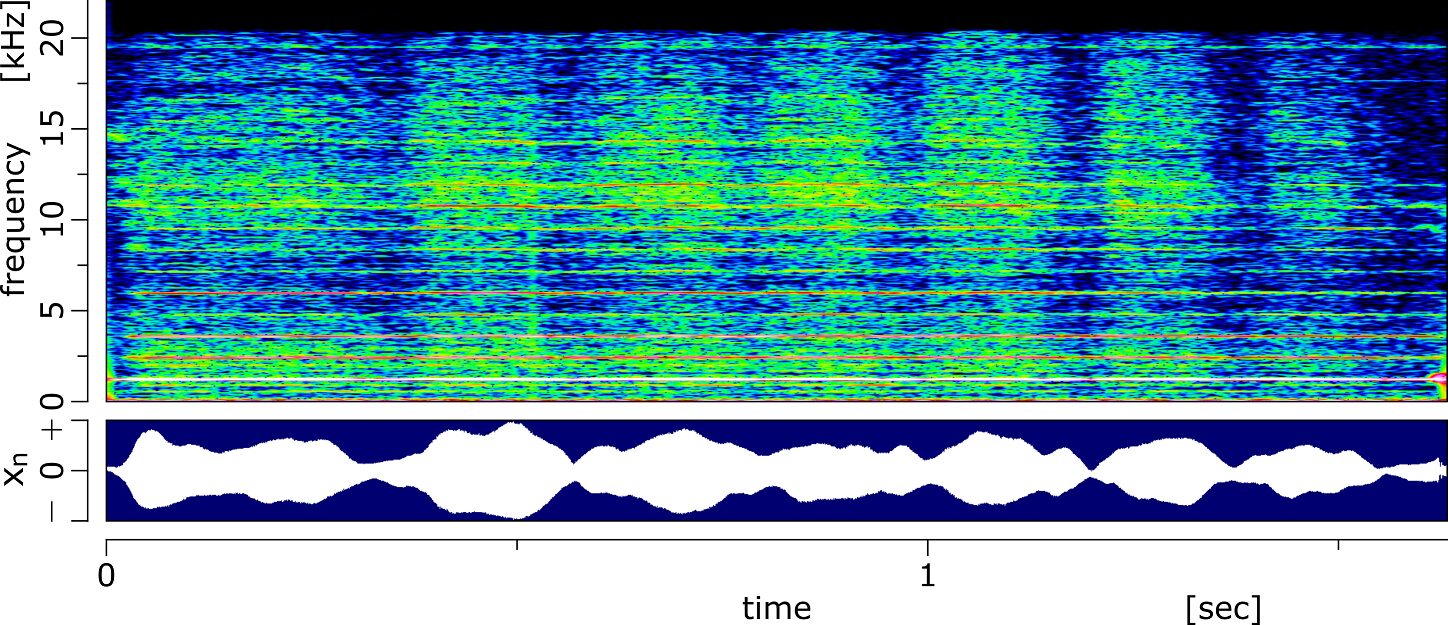
スペクトルグラムを見てみると基本音に比べて倍音の振幅がかなり小さくなっています。また、波形を見てみると時間エンベロープが台形のようになっています。
これらの特徴を持つように部分音ごとに合成をおこない、それらを加算してフルート音を合成します。
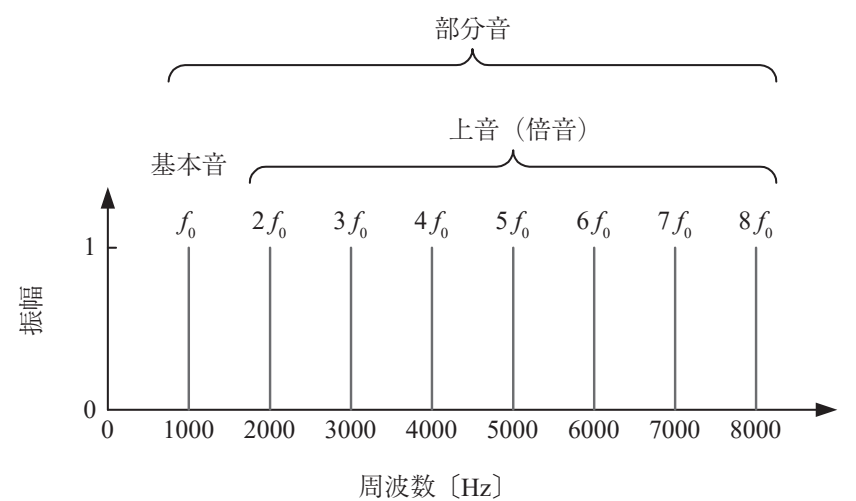
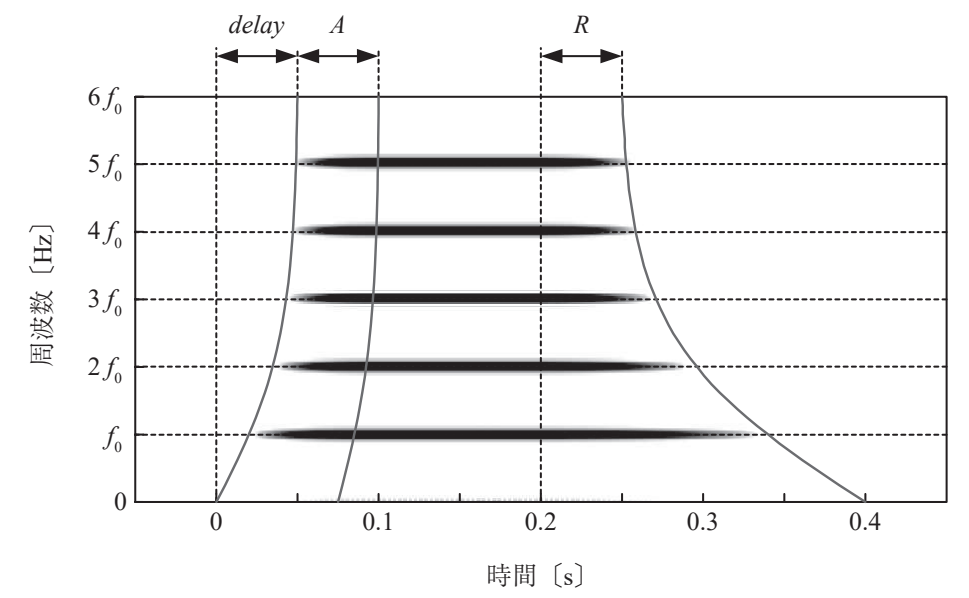
部分音:部分音とは下図のように基本音と倍音を合わせた音のことをいいます。
図:部分音について 引用元:青木直史, ”Python ではじめる音のプログラミング”, 株式会社オーム社, 2022, p.5.
フルート音の合成
合成についてはアナログシンセサイザのしくみを使っていきます。フルートの部分音の合成ブロック図を以下に示します。
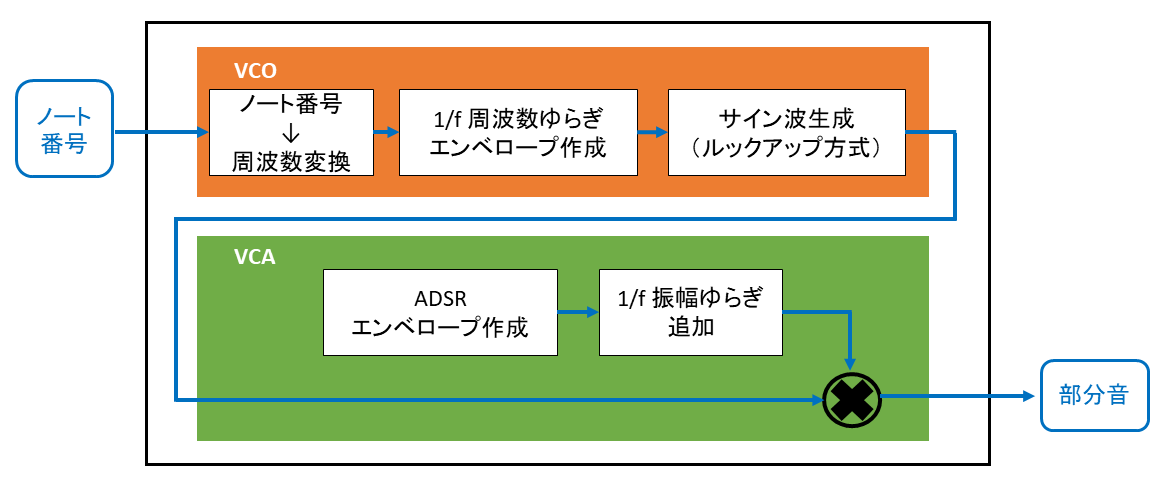
VCO で周波数が微妙に揺らいでいる正弦波を作成して、VCA で台形のような時間エンベロープをもつ波形にしていきます。
上記のブロック図で部分音を作成し、部分音を足し合わせてフルート音を合成します。
VCO
ノート番号→周波数 変換
ノート番号から周波数への変換は以下の計算式で行います。
$$
f_o = 440 \cdot 2^{\left(\cfrac{n_{note}-69}{12}\right)} \tag{1}
$$
ここで、\(n_{note}\) はノート番号です。
1/f 周波数揺らぎ
合成したフルート音が自然に聴こえるように周波数のゆらぎを追加します。周波数のゆらぎの生成ブロック図は以下のようになります。

生成した白色雑音をLPFに通して周波数のゆらぎ \(\Delta f[n]\ \)を生成します。
それから、ノート番号ごとに周波数のゆらぎの大きさを変更いたします。ゆらぎの大きさ\(\ a_{\Delta f}\ \)は以下の計算式で求めます。
\ a_{\Delta f} = \cfrac{p_4}{\left(1 + \exp\left(-\cfrac{(n_{note} - p_1)}{p_3}\right)\right)} + p_2 \tag{2}
$$
\(p_1=108\), \(\ p_2=1\), \(\ p_3=150/12\), \(\ p_4=20\) を代入するとゆらぎの大きさのグラフは以下のようになります。
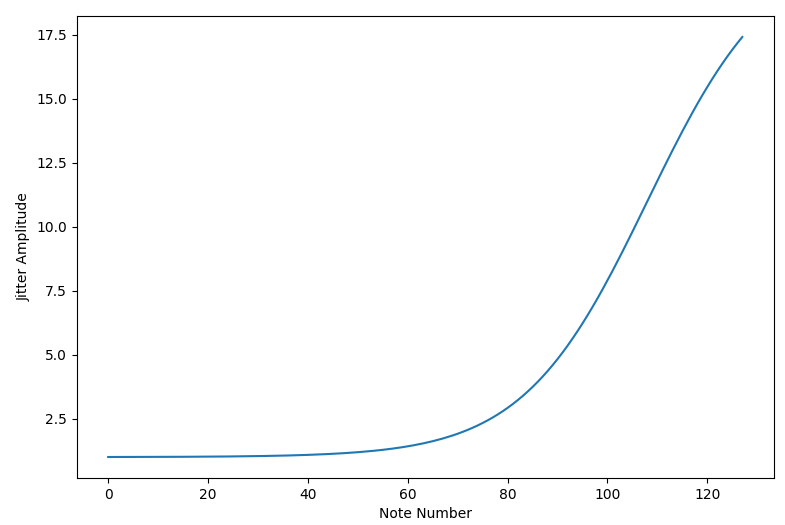
最後に以下の式で揺らいだ周波数を求めます。
$$
f'[n] = f + a_{\Delta f} \cdot \Delta f[n] \tag{3}
$$
サイン波生成
サイン波の生成にはルックアップ方式を用います。
ルックアップ方式を用いたサイン波の生成は以下のようになります。
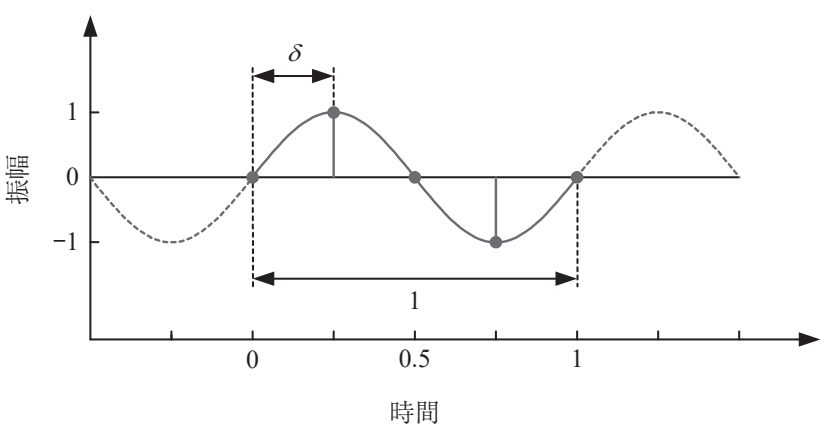
図:ルックアップ方式の更新 引用元:青木直史, ”Python ではじめる音のプログラミング”, 株式会社オーム社, 2022, p.94.
まず、周期 T=1 のサイン波を1周期用意します。それから、\(\ \delta[n]=f'[n]/f_s\ \)分だけ進めていき、進めた箇所の正弦波の値を出力することを繰り返して正弦波を生成します。進んだ先が1より大きい場合は0に戻って、また進ませます。
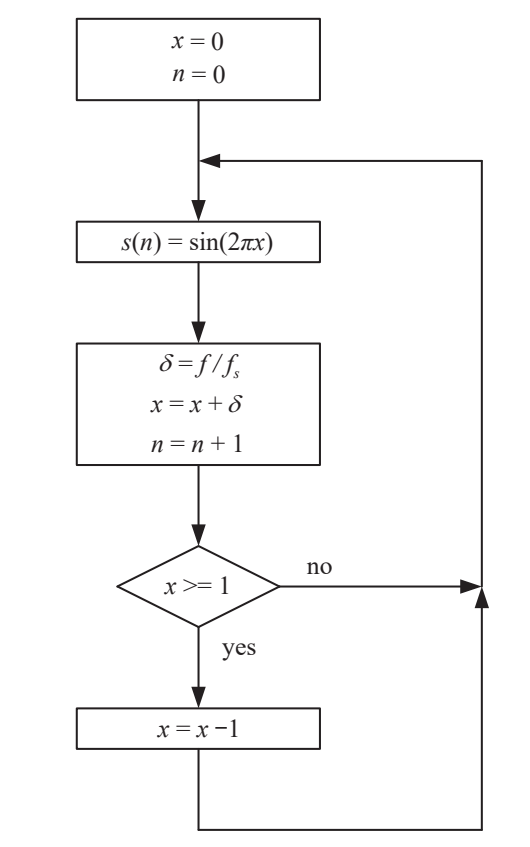
ブロック図は以下のようになります。
図:ルックアップ方式によるサイン波の生成 引用元:青木直史, ”Python ではじめる音のプログラミング”, 株式会社オーム社, 2022, p.94.
この方式の良い点としましては、以下があると思います。
- 周波数が時間変化する正弦波を生成できる
- デジタル回路などを使う場合、三角関数の計算機が必要ない
パソコンで計算する場合は、2つ目のメリットはありませんが、1つ目のメリットのためパソコン上の計算でも使われているかと思います。
また、デジタル回路やマイコンを使う場合、あらかじめメモリに1周期分の正弦波の値を格納しておけば、三角関数の計算機を使う必要がないため、リソースの削減になるというメリットがあります。おまけに値をメモリから取り出すだけのため、計算機を使う場合よりも計算が速くなるというメリットもあります。
VCA
ADSRエンベロープ作成
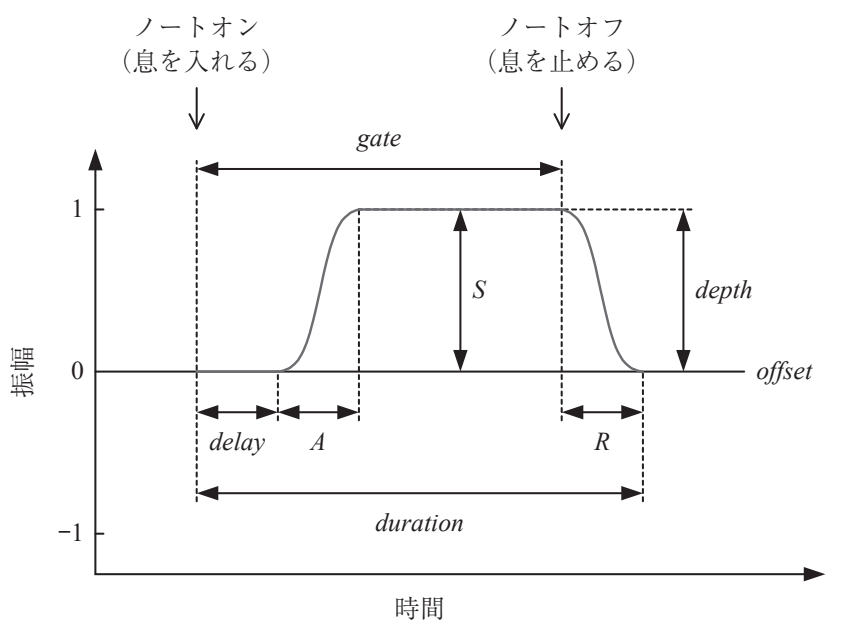
VCAで使用するエンベロープを以下の図のように作成していきます。
図:管楽器の時間エンベロープ 引用元:青木直史, ”Python ではじめる音のプログラミング”, 株式会社オーム社, 2022, p.220.
エンベロープの計算は以下になります。
e[n] =
\left\{
\begin{array}{ll}
0 & (0 \leq n < delay) \\[5pt] S\left(0.5-0.5\cos{\left(\cfrac{\pi(n-delay)}{A}\right)}\right) & (delay \leq n < delay+A) \\[5pt] S & (delay+A \leq n < gate) \\[5pt] S\left(0.5+0.5\cos{\left(\cfrac{\pi(n-gate)}{R}\right)}\right) & (gate \leq n < gate+R) \\[5pt] \end{array} \right. \tag{4} $$
パラメータ delay, A, R については下図のように周波数ごとに設定します。
図:フルート音のスペクトログラムの図 引用元:青木直史, ”Python ではじめる音のプログラミング”, 株式会社オーム社, 2022, p.225
パラメータ delay については(2)式の\(\ n_{note}\ \)を\(\ f\ \)に置き換えて計算します。\(\ p_1=0\), \(\ p_2=-0.1\), \(\ p_3=8000/12\), \(\ p_4=0.2\ \)を代入して計算すると以下のようなグラフになります。
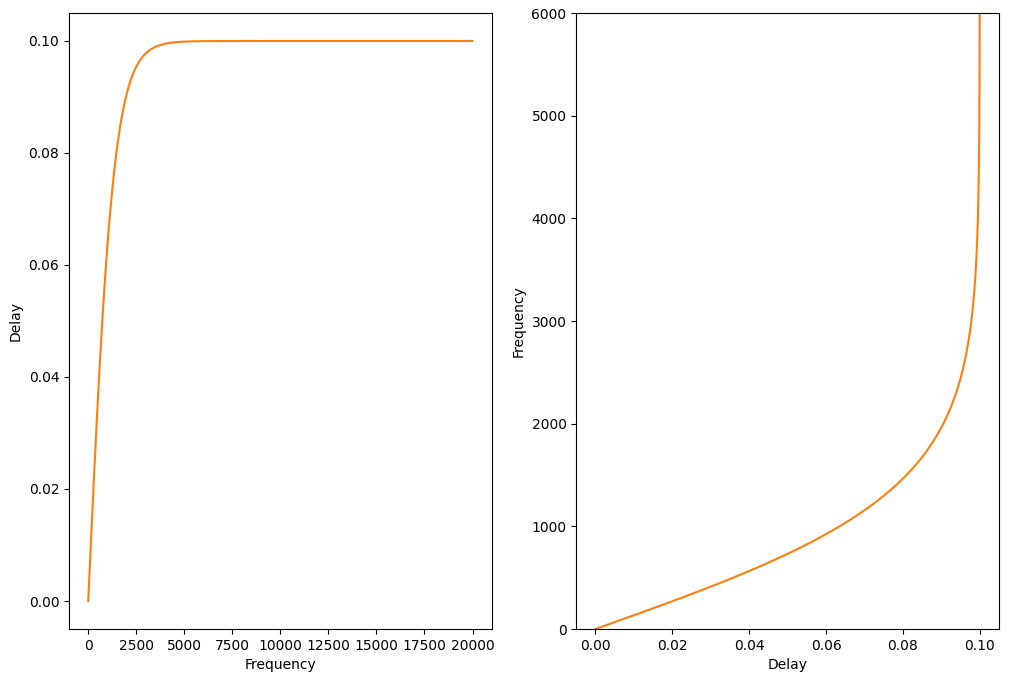
右図のx軸とy軸を反転した図を見ると「フルート音のスペクトログラムの図」の delay と似た形をしているのがわかると思います。
パラメータ A, R については以下の計算式で求めます。
{\rm A,\ R} = \left(1-\cfrac{1}{\left(1 + \exp\left(-\cfrac{(f - p_1)}{p_3}\right)\right)}\right)p_4 + p_2 \tag{5}
$$
表の\(\ p_1\)~\(p_4\ \)を代入するとグラフは以下のようになります。
| A | R | |
|---|---|---|
| \(p_1\) | 0 | 0 |
| \(p_2\) | 0.1 | 0.2 |
| \(p_3\) | 8000/12 | 8000/12 |
| \(p_4\) | 0.2 | 0.4 |
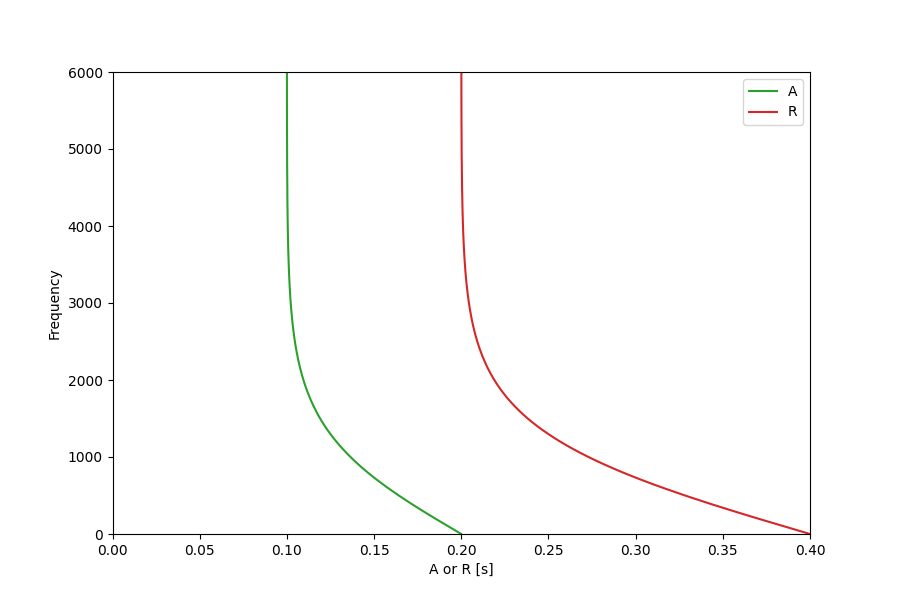
パラメータ S については S=1 とします。
パラメータ depth については参考文献[1]でノート番号と部分音ごとのdepthのテーブルがありましたので、それを使用します。
1/f 振幅揺らぎ
1/f 振幅揺らぎ\(\ \Delta e\ \)についても「3.2. 1/f 周波数ゆらぎ」と同じ手順でゆらぎを生成します。
振幅ゆらぎの大きさについては(2)式の\(\ n_{note}\ \)を「部分音の番号(基本周波数が1番目)」に置き換えて計算します。\(p_1=1\), \(\ p_2=-0.3\), \(\ p_3=10/12\), \(\ p_4=0.8\) を代入するとゆらぎの大きさのグラフは以下のようになります。
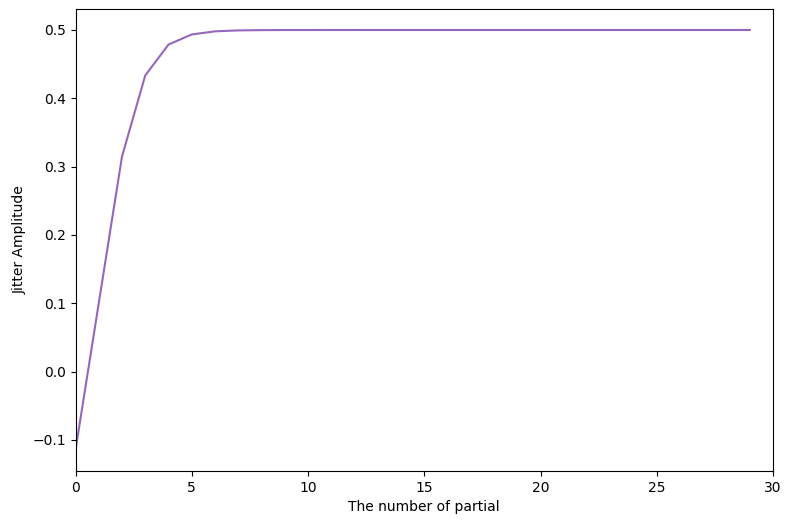
最終的な時間エンベロープは以下のように計算します。
$$
e'[n] = e[n](1+\Delta e[n]) \tag{6}
$$
プログラム
フルートの音を合成するプログラムをPythonで実装しました。ソースコードと実行方法について説明します。
ソースコード
フルートの音を合成するプログラムは以下です。
import numpy as np
import soundfile as sf
import scipy.signal as sg
def calc_2eq( input, p1, p2, p3, p4 ):
output = 1 / (1 + np.exp(-(input - p1) / p3)) * p4 + p2
return output
def calc_5eq( input, p1, p2, p3, p4 ):
output = (1 -1 / (1 + np.exp(-(input - p1) / p3))) * p4 + p2
return output
def gen_flute(fs, note_number, velocity, gate):
"""
ノート番号からフルートの合成データを取得。
Parameters
----------
fs (int) : サンプリング周波数
note_number (int) : ノート番号
velocity (int) : ベロシティ
gate (float) : ノートオンからノートオフの間の時間[s]
Returns
-------
y (np.array) : フルート合成音のデータ
"""
# duration を計算
duration = gate + 1
# 出力データの長さ
length_of_y = int(fs * duration)
y = np.zeros(length_of_y)
# ノート番号から基本周波数を計算
f0 = 440 * np.power(2, (note_number - 69) / 12)
# 部分音の数
number_of_partial = 30
# 時間エンベロープのdepth (ノート番号-59, 部分音)
vca_depth_tbl = np.array([[0.932, 0.042, 0.175, 0.014, 0.029, 0.008, 0.026, 0.015, 0.019, 0.010, 0.008, 0.004, 0.003, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.000, 0.001, 0.000, 0.000, 0.001, 0.000, 0.001, 0.000, 0.001],
[0.932, 0.091, 0.159, 0.021, 0.035, 0.015, 0.039, 0.016, 0.026, 0.010, 0.006, 0.004, 0.002, 0.002, 0.001, 0.001, 0.001, 0.001, 0.001, 0.000, 0.001, 0.000, 0.001, 0.001, 0.001, 0.001, 0.000, 0.001, 0.000, 0.001],
[0.932, 0.150, 0.108, 0.024, 0.040, 0.026, 0.039, 0.014, 0.018, 0.009, 0.002, 0.004, 0.002, 0.003, 0.001, 0.001, 0.001, 0.001, 0.000, 0.000, 0.001, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000],
[0.932, 0.165, 0.086, 0.027, 0.050, 0.033, 0.026, 0.010, 0.007, 0.007, 0.002, 0.003, 0.001, 0.002, 0.001, 0.001, 0.001, 0.001, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000],
[0.932, 0.215, 0.095, 0.032, 0.049, 0.047, 0.015, 0.011, 0.006, 0.006, 0.002, 0.002, 0.002, 0.001, 0.001, 0.001, 0.001, 0.001, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000],
[0.932, 0.448, 0.116, 0.070, 0.079, 0.058, 0.010, 0.009, 0.004, 0.005, 0.002, 0.002, 0.002, 0.001, 0.001, 0.001, 0.001, 0.001, 0.000, 0.000, 0.000, 0.000, 0.001, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000],
[0.932, 0.685, 0.149, 0.130, 0.119, 0.047, 0.012, 0.006, 0.005, 0.005, 0.003, 0.002, 0.002, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.000, 0.000, 0.000, 0.000, 0.001, 0.001],
[0.932, 0.594, 0.226, 0.147, 0.118, 0.046, 0.017, 0.007, 0.009, 0.004, 0.002, 0.002, 0.002, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.000, 0.000, 0.001, 0.001, 0.001, 0.001],
[0.932, 0.532, 0.267, 0.116, 0.113, 0.057, 0.020, 0.007, 0.008, 0.003, 0.002, 0.002, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001],
[0.932, 0.583, 0.190, 0.075, 0.074, 0.036, 0.013, 0.005, 0.004, 0.003, 0.002, 0.002, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001],
[0.932, 0.407, 0.128, 0.052, 0.025, 0.010, 0.005, 0.003, 0.002, 0.002, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.000, 0.000, 0.000, 0.000, 0.000, 0.001, 0.001, 0.000, 0.001, 0.000, 0.000, 0.000, 0.000],
[0.932, 0.213, 0.118, 0.039, 0.015, 0.006, 0.003, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000],
[0.932, 0.156, 0.105, 0.042, 0.014, 0.004, 0.002, 0.002, 0.001, 0.001, 0.001, 0.001, 0.001, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000],
[0.932, 0.128, 0.110, 0.063, 0.014, 0.004, 0.002, 0.002, 0.001, 0.001, 0.001, 0.001, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000],
[0.932, 0.092, 0.120, 0.051, 0.012, 0.004, 0.002, 0.001, 0.001, 0.000, 0.001, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000],
[0.932, 0.063, 0.107, 0.024, 0.007, 0.002, 0.001, 0.001, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000],
[0.932, 0.057, 0.093, 0.017, 0.004, 0.001, 0.001, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000],
[0.932, 0.068, 0.077, 0.013, 0.004, 0.001, 0.001, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000],
[0.932, 0.105, 0.051, 0.007, 0.004, 0.002, 0.001, 0.001, 0.001, 0.001, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000],
[0.932, 0.161, 0.053, 0.005, 0.002, 0.002, 0.001, 0.001, 0.001, 0.001, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000],
[0.932, 0.176, 0.065, 0.003, 0.003, 0.002, 0.001, 0.001, 0.001, 0.000, 0.000, 0.000, 0.001, 0.001, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000],
[0.932, 0.139, 0.049, 0.003, 0.003, 0.001, 0.001, 0.000, 0.000, 0.000, 0.000, 0.000, 0.001, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000],
[0.932, 0.087, 0.038, 0.002, 0.002, 0.000, 0.000, 0.001, 0.000, 0.000, 0.000, 0.000, 0.001, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000],
[0.932, 0.089, 0.052, 0.006, 0.004, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000],
[0.932, 0.194, 0.089, 0.017, 0.009, 0.003, 0.003, 0.002, 0.002, 0.001, 0.002, 0.001, 0.001, 0.001, 0.001, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000],
[0.932, 0.248, 0.103, 0.022, 0.011, 0.004, 0.004, 0.002, 0.002, 0.002, 0.002, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000],
[0.932, 0.148, 0.067, 0.013, 0.006, 0.003, 0.003, 0.001, 0.001, 0.002, 0.001, 0.001, 0.001, 0.000, 0.001, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000],
[0.932, 0.070, 0.036, 0.006, 0.004, 0.002, 0.001, 0.001, 0.002, 0.002, 0.001, 0.001, 0.001, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000],
[0.932, 0.082, 0.030, 0.006, 0.006, 0.003, 0.001, 0.001, 0.005, 0.002, 0.001, 0.001, 0.001, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000],
[0.932, 0.077, 0.034, 0.007, 0.005, 0.002, 0.001, 0.002, 0.005, 0.001, 0.001, 0.001, 0.001, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000],
[0.932, 0.041, 0.035, 0.006, 0.005, 0.002, 0.002, 0.002, 0.002, 0.001, 0.001, 0.001, 0.001, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000],
[0.932, 0.020, 0.024, 0.003, 0.003, 0.002, 0.002, 0.003, 0.001, 0.001, 0.001, 0.001, 0.001, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000],
[0.932, 0.019, 0.024, 0.005, 0.003, 0.002, 0.002, 0.002, 0.001, 0.001, 0.001, 0.001, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000],
[0.932, 0.019, 0.028, 0.008, 0.003, 0.002, 0.003, 0.001, 0.001, 0.001, 0.001, 0.001, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000],
[0.932, 0.023, 0.023, 0.006, 0.003, 0.009, 0.003, 0.002, 0.002, 0.002, 0.003, 0.001, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000],
[0.932, 0.038, 0.029, 0.006, 0.005, 0.021, 0.005, 0.004, 0.004, 0.004, 0.006, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000],
[0.932, 0.046, 0.037, 0.007, 0.006, 0.026, 0.007, 0.005, 0.005, 0.005, 0.006, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000],
[0.932, 0.046, 0.037, 0.007, 0.006, 0.026, 0.007, 0.005, 0.005, 0.004, 0.002, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000],
[0.932, 0.046, 0.037, 0.007, 0.006, 0.026, 0.007, 0.005, 0.005, 0.002, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0.000]])
# VCO で使用する値をあらかじめ計算
freq = np.arange(1, number_of_partial + 1) * f0
a_freq_jitter = calc_2eq( note_number, p1=108, p2=1, p3=150/12, p4=20 )
# VCA で使用する値をあらかじめ計算
vca_S = np.ones(number_of_partial)
vca_delay = calc_2eq( freq, p1=0, p2=-0.1, p3=8000/12, p4=0.2 )
vca_A = calc_5eq( freq, p1=0, p2=0.1, p3=8000/12, p4=0.2 )
vca_R = calc_5eq( freq, p1=0, p2=0.2, p3=8000/12, p4=0.4 )
a_amp_jitter = calc_2eq( freq/f0, p1=1, p2=-0.3, p3=10/12, p4=0.8 )
vca_depth = vca_depth_tbl[note_number-59, :]
# 部分音ごとに計算
for i in range(number_of_partial):
#----------------------------------------------
# VCO
#----------------------------------------------
## 白色雑音生成(周波数ゆらぎ生成)
random = np.random.rand(length_of_y)*2 - 1
## LPF(周波数ゆらぎ生成)
fc = 40
b, a = sg.iirfilter(2, fc/(fs//2), btype='lowpass')
jitter = sg.lfilter(b, a, random )
jitter /= np.max(np.abs(jitter))
## 揺らぎの大きさ変更(周波数ゆらぎ生成)
f_vco = freq[i] + a_freq_jitter * jitter
## ルックアップ方式によるサイン波生成
sin_wave = np.zeros(length_of_y)
x = 0
for n in range(length_of_y):
sin_wave[n] = np.sin(2 * np.pi * x)
delta = f_vco[n] / fs
x += delta
if x >= 1:
x -= 1
#----------------------------------------------
# VCA
#----------------------------------------------
## エンベロープ作成
env = np.zeros(length_of_y)
delay_n = int(vca_delay[i] * fs)
A_n = int(vca_A[i] * fs)
R_n = int(vca_R[i] * fs)
gate_n = int(gate * fs)
duration_n = int(duration * fs)
for n in range(delay_n, delay_n + A_n):
env[n] = vca_S[i] * (0.5 - 0.5 * np.cos(np.pi * (n - delay_n) / A_n))
for n in range(delay_n + A_n, gate_n):
env[n] = vca_S[i]
for n in range(gate_n, min(gate_n + R_n, duration_n)):
env[n] = vca_S[i] * (0.5 + 0.5 * np.cos(np.pi * (n - gate_n) / R_n))
env *= vca_depth[i]
## 白色雑音生成(振幅ゆらぎ生成)
random = np.random.rand(length_of_y)*2 - 1
## LPF(振幅ゆらぎ生成)
fc = 40
b, a = sg.iirfilter(2, fc/(fs//2), btype='lowpass')
jitter = sg.lfilter(b, a, random )
jitter /= np.max(np.abs(jitter))
## 揺らぎの大きさ変更(振幅ゆらぎ生成)
env_vca = env * ( 1 + a_amp_jitter[i] * jitter)
## 部分音生成
y += sin_wave * env_vca
#----------------------------------------------
y *= velocity / 127 / np.max(np.abs(y))
return y
# パラメータ
note_number_list = [60, 62, 64, 65, 67, 69, 71, 72] #ノート番号(C4-C5)
fs = 48000 # サンプリング周波数
velocity = 100 # ベロシティ
gate = 1 # ノートオン~ノートオフの期間
interval = int( fs*0.5 ) # 音の間隔
wav_out_name = "flute_synth.wav" # 出力WAVファイル名
# 出力データ初期化
y = np.zeros( interval )
interval_data = np.zeros( interval )
for i, note_number in enumerate( note_number_list ):
# フルートの音を合成
flute_sound = gen_flute(fs, note_number, velocity, gate)
# フルートの合成音を出力データに追加
y = np.append( y, flute_sound )
y = np.append( y, interval_data ) # インターバル追加
sf.write(wav_out_name, y, fs, subtype='PCM_16')43~82行目:VCAで作成するエンベロープのdepthのテーブルです。
84~94行目:for文の前に計算できる値はあらかじめ計算しておきます。
158行目:ベロシティによって音の大きさを変更しています。
実行方法
(1) プログラムを実行するディレクトリにソースコード(flute_synth.py)を格納する。
(2) ソースコード162~168行目のパラメータと出力データ名を変更する。
# パラメータ
note_number_list = [60, 62, 64, 65, 67, 69, 71, 72] #ノート番号(C4-C5)
fs = 48000 # サンプリング周波数
velocity = 100 # ベロシティ
gate = 1 # ノートオン~ノートオフの期間
interval = int( fs*0.5 ) # 音の間隔
wav_out_name = "flute_synth.wav" # 出力WAVファイル名
(3) 以下のコマンドで python を実行することで、フルートの合成音のWAVデータが出力される。
$ python flute_synth.py処理結果
上記のソースコードでドレミファソラシドのフルート音を合成いたしました。
フルートの合成音は以下になります。
フルート合成音
波形とスペクトログラムは以下です。
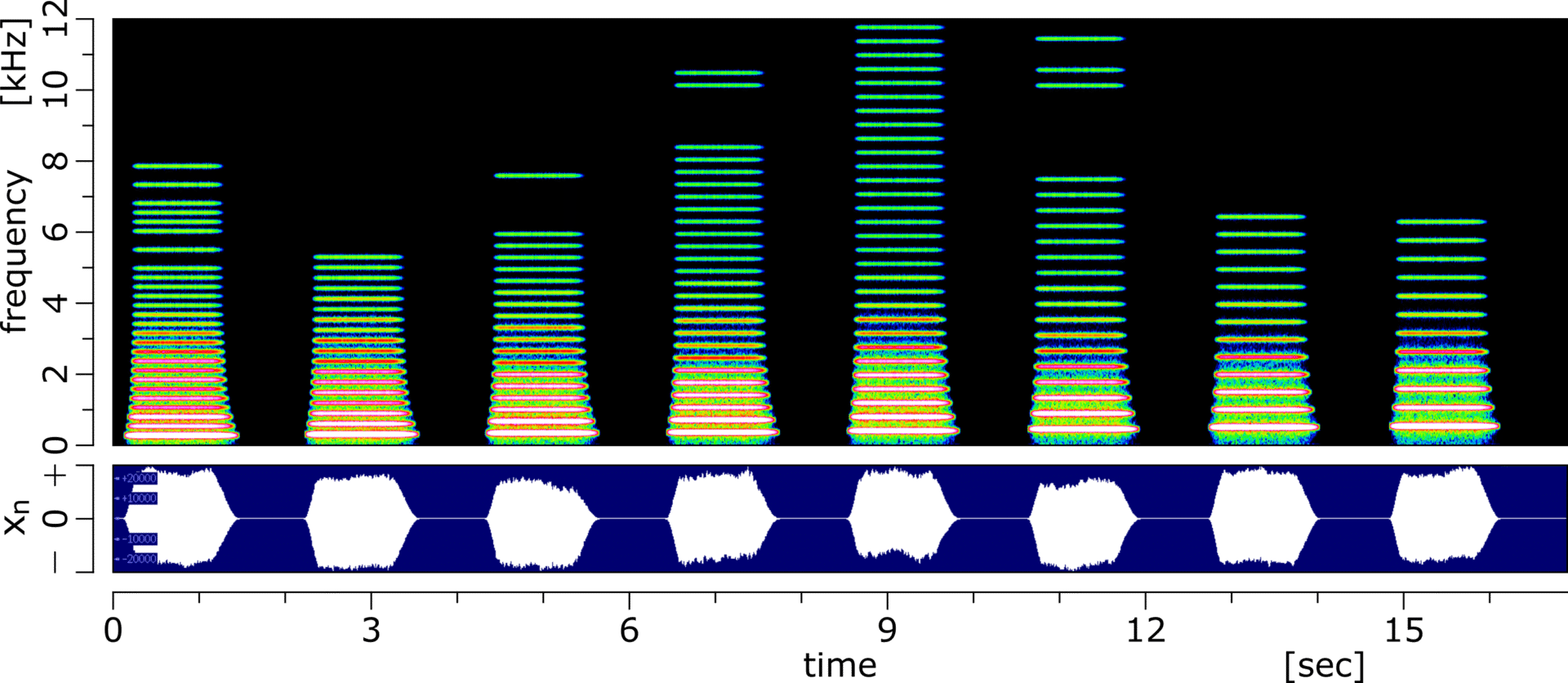
スペクトログラムを見比べてパラメータを調整すればもっとよくなりそうな気がします。
おわりに
本記事ではアナログシンセサイザーのしくみを用いてフルート音の合成を行いました。
アナログシンセサイザーのしくみを使えば、ほとんどの楽器を合成できそうですが、パラメータの調整がかなり大変だなと感じました。
時間があればMIDIデータを使って少し演奏してみたいと思います。
参考文献
[1] 青木直史, ”Python ではじめる音のプログラミング”, 株式会社オーム社, 2022.