本記事では、ヒルベルト変換についてまとめてみました。Python でヒルベルト変換を使った包絡線と瞬時周波数を求めるソースコードを作成しましたので、その処理結果について確認していきます。
ヒルベルト変換とは
ヒルベルト変換は端的にいえば、信号のすべての周波数成分の位相を \(\pi/2\) (90度)遅らせる処理となります[1]。
離散時間における周波数領域のヒルベルト変換は以下です。
$$
\begin{align}
&\hat{X}[k] = -j\ {\rm sgn}(k) X[k] \hspace{1em} \tag{1} \\[8pt]
&\left(k=-\frac{N-1}{2},\cdots ,\frac{N-1}{2}\right)
\end{align}
$$
ここで、\(X[k]\ \)は離散時間の周波数成分、\(k\ \)は周波数ビン番号、\(N\ \)はFFT点数、\({\rm sgn(\cdot)}\ \)は以下の式で表される符号関数となります。
$$
{\rm sgn}(k) =
\begin{cases}
1 & (k>0) \\[5pt]
0 & (k=0) \\[5pt]
-1 & (k<0)
\end{cases} \tag{2}
$$
Python でヒルベルト変換を行う場合は以下のように書けます。
# ヒルベルト変換
def hilbert(x):
# === FFT ===
fft = np.fft.rfft(x)
N = fft.shape[0] # FFT点数/2 を取得
# === ヒルベルト変換(周波数領域) ===
fft[1:N-1] = -1j*fft[1:N-1]
# === IFFT ===
x_hat = np.fft.irfft(fft)
return x_hat
np.fft.rfft, np.fft.irfftを使うことで、負の周波数成分については正の周波数成分の複素共役から計算されるため、計算を省略できます。
補足:連続時間のヒルベルト変換を考えると、\(-j\ {\rm sgn}(f)\ \)の逆フーリエ変換
$$
\begin{equation}
F^{-1}\{-j\ {\rm sgn(f)}\} = \frac{1}{\pi t} \tag{3}
\end{equation}
$$
から時間領域のヒルベルト変換は \(1/(\pi t)\ \)と\(\ x(t)\ \)の畳み込み演算によって以下のように求められます。
$$
\begin{equation}
\hat{x}(t) = \frac{1}{\pi}\int_{-\infty}^{\infty}\frac{1}{t-\tau}x(\tau)d\tau \tag{4}
\end{equation}
$$
上記の式についてはヒルベルト変換の公式として知られています。
ヒルベルト変換の用途
ヒルベルト変換の用途としては主に以下の2つです。
- 包絡線の抽出
- 瞬時位相・瞬時周波数の解析
これらの用途で、ヒルベルト変換は医用分野や通信分野で主に使われているそうです。医用分野では脳波の解析など、通信分野では変調・復調に使われます。
筆者の印象では、ヒルベルト変換が音響信号処理において使われているイメージはないです。ただ、ChatGPTによれば、トランジェント検出やステレオフェイザーなどで使われているみたい。
ソースコード
包絡線・瞬時周波数を解析するソースコードを作成しました。
import numpy as np
import matplotlib.pyplot as plt
import soundfile as sf
# ヒルベルト変換
def hilbert(x):
# === FFT ===
fft = np.fft.rfft(x)
N = fft.shape[0] # FFT点数/2 を取得
# === ヒルベルト変換(周波数領域) ===
fft[1:N-1] = -1j*fft[1:N-1]
# === IFFT ===
x_hat = np.fft.irfft(fft, n=len(x))
return x_hat
# WAVファイルを読み込む
x, fs = sf.read("input.wav")
# ヒルベルト変換
x_hat = hilbert(x)
# 包絡線作成
envelope = np.sqrt(x*x + x_hat*x_hat)
# 瞬時周波数の解析
phase = np.arctan2(x_hat, x)
phase = np.unwrap(phase)
freq = fs * np.diff(phase) / (2.0*np.pi)
## プロット
n1 = np.arange(len(x))
n2 = np.arange(len(x)-1)
fig=plt.figure(figsize=(10,8))
### 包絡線のプロット
ax1 = fig.add_subplot(211)
ax2 = fig.add_subplot(212)
ax1.plot(n1/fs, x, label='Signal')
ax1.plot(n1/fs, envelope, label='Envelope', linewidth=2)
ax1.set_xlim(0, len(x)/fs)
ax1.set_ylim(-1, 1)
ax1.set_xlabel("time [s]")
ax1.set_ylabel("x")
ax1.legend()
### 瞬時周波数のプロット
ax2.plot(n2/fs, freq, label='Frequency')
ax2.set_xlim(0, len(x)/fs)
ax2.set_ylim(0, 1000)
ax2.set_xlabel("time [s]")
ax2.set_ylabel("frequency [Hz]")
ax2.legend()
fig.savefig("graph.png")
包絡線の抽出
包絡線の抽出は、ヒルベルト変換で作成した直交波形 \(\ \hat{x}[n]\ \)ともとの波形 \(\ x[n]\ \)との2乗和の平方根((5)式)を計算することで求められます。
$$
\begin{equation}
envelope = \sqrt{x^{2}[n] + \hat{x}^{2}[n]} \tag{5}
\end{equation}
$$
ソースコードでは次の箇所にあたります。
# 包絡線作成
envelope = np.sqrt(x*x + x_hat*x_hat)
これで包絡線を抽出できる理由としては、\(x[n]=a\cos{(\omega n)}\ \)のように狭帯域信号の場合、直交波形は \(\ \hat{x}[n]=a\sin{(\omega n)}\ \)となり、
$$
\begin{align}
&\sqrt{x^{2}[n] + \hat{x}^{2}[n]} \\[5pt]
= &\sqrt{a^2\cos^2{(\omega n)} + a^2\sin^2{(\omega n)}} \\[5pt]
= &a \tag{6}
\end{align}
$$
で包絡線が抽出されるからです。
包絡線を抽出した結果が以下になります。
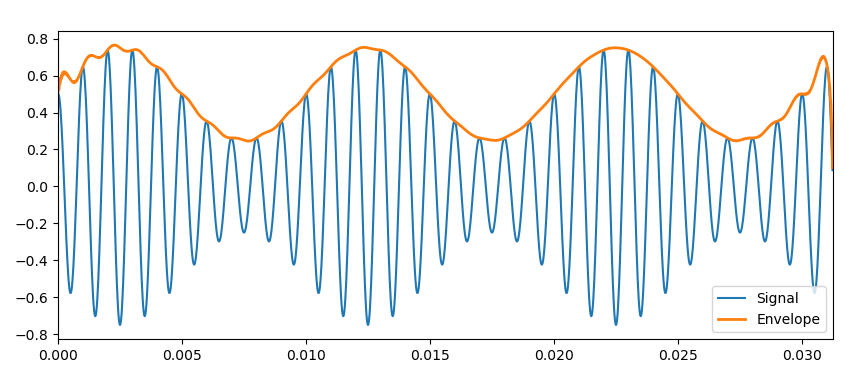
包絡線がうまく抽出されているのがわかると思います。
ただし、音声のような広帯域信号に対してヒルベルト変換の包絡線抽出を適用すると以下のように上手く包絡線が作成されません。
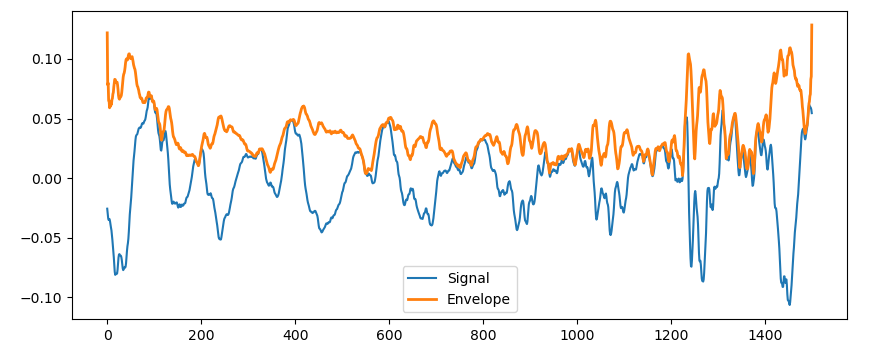
広帯域信号を包絡線抽出する場合、フィルタをかけて狭帯域信号にする必要があります。
瞬時周波数の計算
瞬時周波数については以下の手順で求められます。
1.瞬時位相 \(\theta[n]\ \)を以下の式から計算
$$
\theta[n] = \tan^{-1} \left(\frac{\hat{x}[n]}{x[n]}\right) \tag{7}
$$
2.隣り合うサンプルの位相差分を\(\ 2\pi\ \)で割って、サンプルレート \(\ F_{s}\ \)を掛けることで瞬時周波数を計算
$$
f[n] = \frac{\theta[n+1]-\theta[n]}{2\pi} F_{s} \tag{8}
$$
ソースコードでは次の箇所です。
# 瞬時周波数の解析
phase = np.arctan2(x_hat, x)
phase = np.unwrap(phase)
freq = fs * np.diff(phase) / (2.0*np.pi)
(7)式で瞬時位相を計算できる理由としては、先ほどと同様に\(\ x[n]=a\cos{(\omega n)}\ \)、\(\ \hat{x}[n]=a\sin{(\omega n)}\ \)の場合、
$$
\begin{align}
\tan^{-1} \left(\frac{a\sin{(\omega n)}}{a\cos{(\omega n)}}\right) &= \tan^{-1} \left(\tan{\theta}\right) \\[5pt]
&= \theta \tag{9}
\end{align}
$$
となり、位相を求められるからです。位相を微分することで周波数が求められます。
100Hz~1000Hzのチャープ信号に対して瞬時周波数を計算したグラフは以下となります。
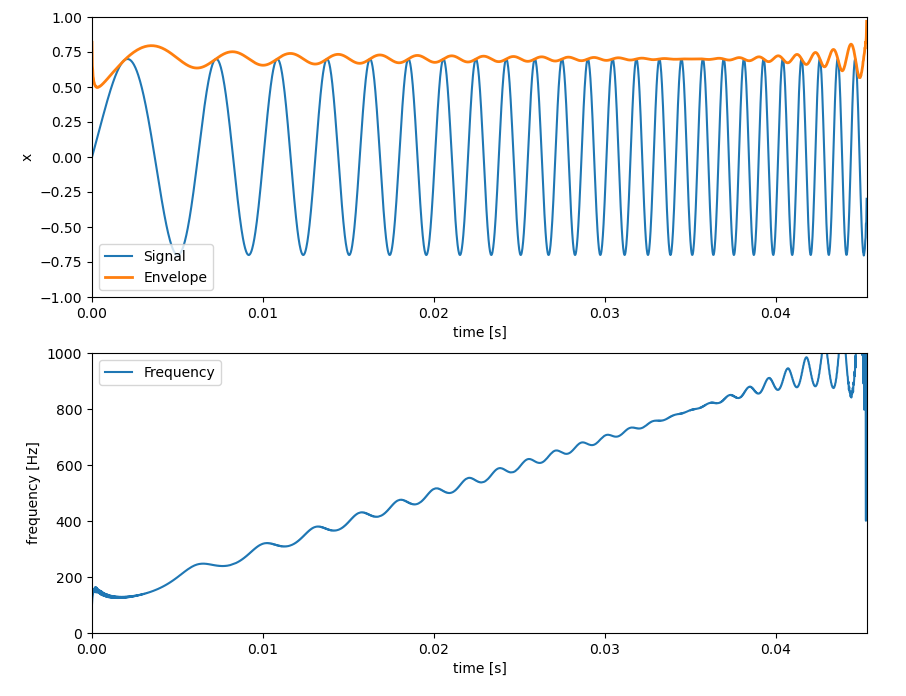
瞬時周波数は少し揺れていますが、きちんと求められます。
ヒルベルト変換の応用
ヒルベルト変換の音響信号処理への応用についてみていきます。
トランジェント検出
ChatGPTにトランジェント検出のソースコードを作っていただきました。
トランジェント検出のソースコード(クリックで展開)
import numpy as np
import scipy.signal as signal
import matplotlib.pyplot as plt
import soundfile as sf
# 音声読み込み
x, fs = sf.read("input.wav")
if x.ndim > 1:
x = x[:,0]
# ヒルベルト変換で包絡線抽出
analytic = signal.hilbert(x)
envelope = np.abs(analytic)
# 平滑化(移動平均)
win = 200
smoothed = np.convolve(envelope, np.ones(win)/win, mode='same')
# 微分 + しきい値
diff = np.diff(smoothed)
threshold = np.mean(diff) + 2 * np.std(diff)
transient_points = np.where(diff > threshold)[0]
# プロット
plt.figure(figsize=(10,4))
plt.plot(x, label="signal")
plt.plot(smoothed, label="envelope", alpha=0.7)
plt.scatter(transient_points, smoothed[transient_points], color="r", label="transients")
plt.legend()
plt.show()
1.ヒルベルト変換で包絡線を抽出。
# ヒルベルト変換で包絡線取得
analytic = signal.hilbert(x)
envelope = np.abs(analytic)
2.包絡線に対して200点の矩形窓を畳み込んで平滑化。
# 平滑化(移動平均)
win = 200
smoothed = np.convolve(envelope, np.ones(win)/win, mode='same')
3.隣接する信号値の差分が平均値+標準偏差の2倍以上だったらトランジェントの判定をする。
# 微分 + しきい値
diff = np.diff(smoothed)
threshold = np.mean(diff) + 2 * np.std(diff)
transient_points = np.where(diff > threshold)[0]
Audacityで作成したリズムトラックの音に対してトランジェント検出した結果は以下となります。
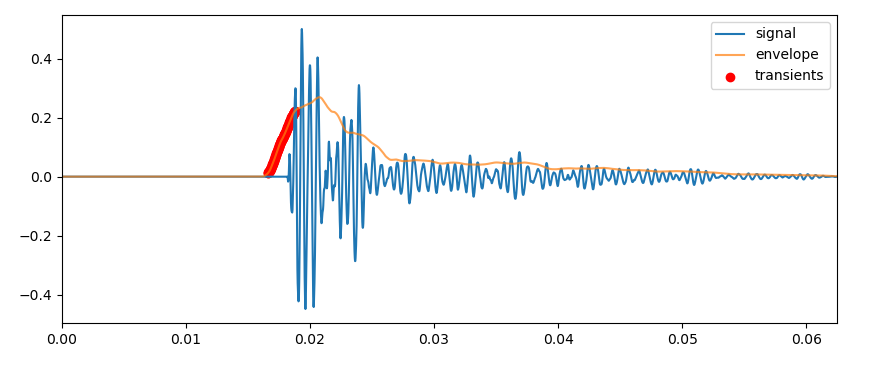
包絡線やトランジェント検出点を見ると、トランジェント検出の精度は高そうに見えます。
広帯域の包絡線の抽出が上手くいってなかったので、あまり期待していなかったのですが、平滑化することで結構よくなってそうです。
ステレオフェイザー
ステレオフェイザーは音に”揺らぎ”を加える空間系エフェクトの一種です。左右のステレオ感を強調するために主に使われます。
ステレオフェイザーのブロック図は以下です[2]。
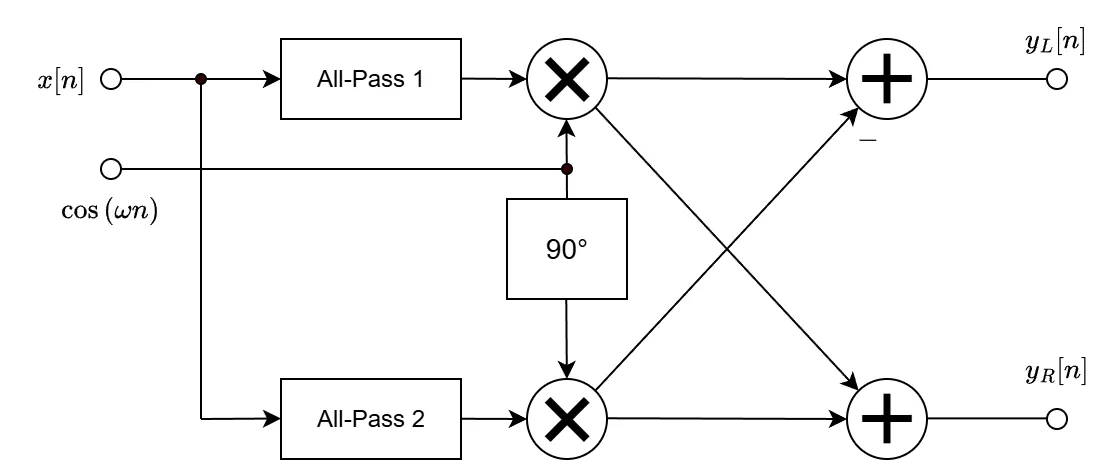
ステレオフェイザーでは、
- 位相ずれ信号と元の信号を混ぜることでうねりを発生
- 左右チャンネルでLFOの位相をずらして、信号のくぼみが時間的にずれる
これで、音が空間を回るように聞こえます。
ChatGPT で作成したステレオフェイザーのソースコードを少し変更したものが以下です(クリックで展開)。
ステレオフェイザーのソースコード(クリックで展開)
import numpy as np
import soundfile as sf
from scipy.signal import hilbert
# パラメータ
lfo_freq=1.0
depth=1.0
mix=0.8
# WAV読み込み
x, fs = sf.read("clean-guitar2.wav")
N = x.shape[0]
t = np.arange(N) / fs
# ヒルベルト変換
xa = hilbert(x)
x = np.real(xa)
x_hat = np.imag(xa) # 90deg shifted version
# LFO
omega = 2 * np.pi * lfo_freq
carrier_cos = depth * np.cos(omega * t)
carrier_sin = depth * np.sin(omega * t)
y_real = x * carrier_cos - x_hat * carrier_sin
y_imag = x * carrier_sin + x_hat * carrier_cos
# ピークを 0.9 にする
peak = max(np.max(np.abs(y_real)), np.max(np.abs(y_imag)), 1e-9)
y_real = y_real / peak * 0.9
y_imag = y_imag / peak * 0.9
# Mix dry and wet
left = (1.0 - mix) * x + mix * y_real
right = (1.0 - mix) * x + mix * y_imag
# Stack to stereo
y = np.vstack((left, right)).T
# final normalization (avoid clipping)
maxval = np.max(np.abs(y))
if maxval > 0.9999:
y = y / maxval * 0.9999
# WAV書き込む
sf.write("out.wav", y, fs, subtype="PCM_24")
1.ヒルベルト変換した信号(All-Pass2を通した信号)を作成。All-Pass1は何もしない。
# ヒルベルト変換
xa = hilbert(x)
x = np.real(xa)
x_hat = np.imag(xa)
2.LFOである \(\ \cos{(\omega n)}, \sin{(\omega n)}\ \) とAll-Passを通った信号から、出力信号\(\ y_{L}[n], y_{R}[n]\ \)を作成。
# LFO
omega = 2 * np.pi * lfo_freq
carrier_cos = depth * np.cos(omega * t)
carrier_sin = depth * np.sin(omega * t)
y_real = x * carrier_cos - x_hat * carrier_sin
y_imag = x * carrier_sin + x_hat * carrier_cos
3.元の信号 \(\ x[n]\ \) と出力信号 \(\ y[n]\ \)をミックスする。
# Mix dry and wet
left = (1.0 - mix) * x + mix * y_real
right = (1.0 - mix) * x + mix * y_imag
ステレオフェイザーを適用したギター音は以下となります。
・入力(ギター音)
・出力(ステレオフェイザー適用後)
おわりに
本記事では、ヒルベルト変換についてまとめました。ヒルベルト変換はデジタル信号処理で度々聞く用語ですので、デジタル信号処理を勉強している人は覚えておいてもよいかなと思います。
ただ、音響信号処理では頻繁に使用するものではないかな...。
■参考文献
[1] 城戸健一, ”ディジタルフーリエ解析(Ⅱ) ー上級編ー,” コロナ社, 2007.
[2] U.Zölzer(編), "DAFX: Digital Audio Effects. 2nd ed.," John Wiley & Sons, 2011.
■使用した楽曲について
この記事で信号処理した楽曲は Pixabay で提供されているものを使用させていただきました。
Music: "electric guitar chords5" by freesound_community — Pixabay
https://pixabay.com/sound-effects/electric-guitar-chords5-34367/
