
ヘリウムガスを吸い込んだときの特徴的な声はヘリウムボイスと呼ばれています。本記事では、信号処理でヘリウムボイスを擬似的に実現してみました。前回の記事で紹介したケプストラム分析を用いてスペクトル包絡の加工をします。
ヘリウムボイスの原理
参考文献 [1] によると、ヘリウムボイスは、ヘリウムガスを吸い込むことで音速が増大し、声道の共鳴周波数が変化することによって生じる現象のようです。
片方が閉じた管で人間の声道をモデル化して考えます。図のように管の長さが L [m] のとき、波長が\(\ \lambda=4L\) となる周波数、およびその奇数倍の周波数で共鳴が起こります。
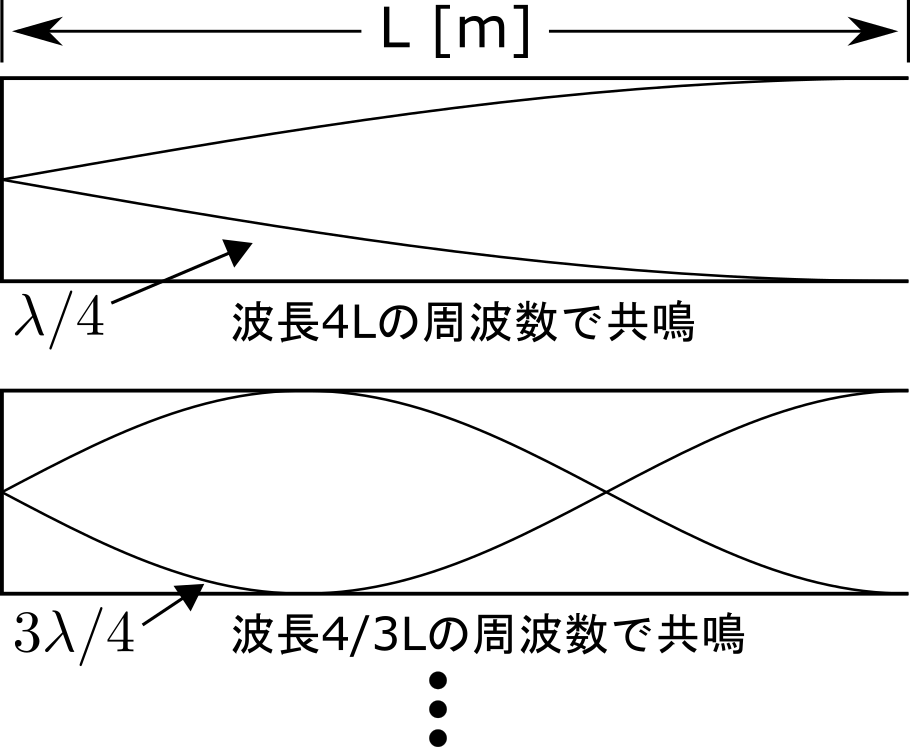
音速 c [m/s]、周波数 f [Hz]、波長 λ [m] には次式のような関係がありますので、
$$
c = f \lambda
$$
音速が r 倍になれば、共鳴する周波数は以下のようになります。
$$
f = \frac{rc}{4L} n \hspace{1em} (n=1,3,5,\cdots)
$$
したがって、音速が増大すれば共鳴周波数(フォルマント周波数)も大きくなるので、ヘリウムボイスはあのような特徴的な音声になります。
ヘリウムボイスの作成方法
ヘリウムボイスを信号処理で擬似的に実現する方法について説明したいと思います。
スペクトル包絡の伸縮
ヘリウムボイスの原理からフォルマント周波数をr倍、つまり対数スペクトル包絡\(H[k]\) を図のように周波数方向に r 倍伸縮すればヘリウムボイスを実現できます。
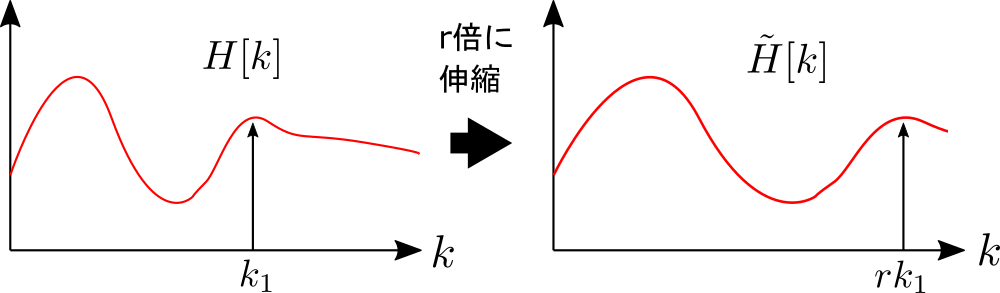
数式で表現すると以下のようになります。
$$
\tilde{H}[k]=H\left[\frac{k}{r}\right]
$$
しかし、k/r が整数になることはあまりないため、以下のような線形補間で\(\ \tilde{H}[k]\ \) を求めます。
$$
\tilde{H}[k]=(1-\alpha_k)H[k'] +\alpha_k H[k'+1]
$$
ただし、
$$
\begin{align}
\hspace{2em} k' &= \left\lfloor \frac{k}{r} \right\rfloor \\
\hspace{2em} \alpha_k &= \frac{k}{r} - k'
\end{align}
$$
参考文献 [1] によると、ヘリウムは空気の約3倍の音速ですが、市販のヘリウムガスは安全のため空気が混入しているそうです。そのため、1.5<r<2.0 としたときが実際のヘリウムボイスに近いみたいです。
ヘリウムボイス変換の流れ
音声をヘリウムボイスに変換するためのブロック図を以下に示します。
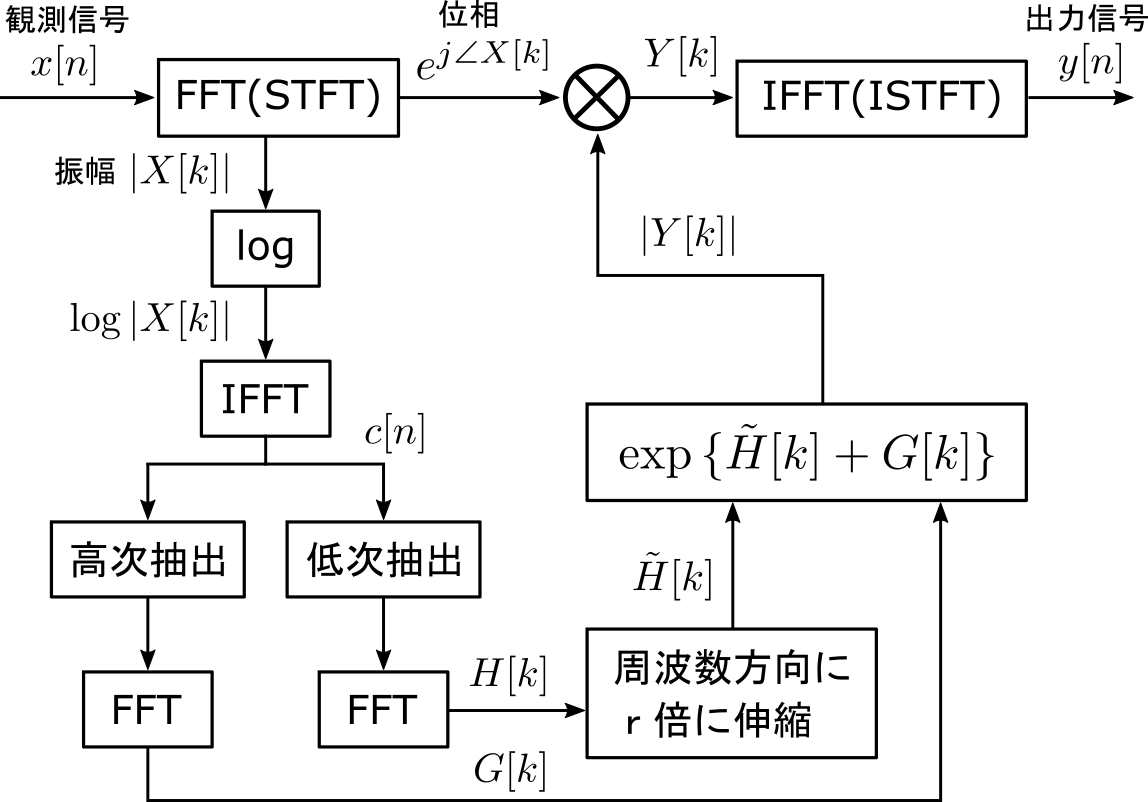
フレームごとにケプストラム分析で対数スペクトル包絡を求めて、r倍に伸縮しています。抽出していなかった高次のケプストラムについてもFFTして、伸縮した対数スペクトルに加算しています。それから、log の逆関数であるexpによって振幅を再合成します。位相については観測信号の位相をそのまま用いています。
プログラム
音声をヘリウムボイスに変換するソースコードは以下となっています。
import soundfile as sf
import numpy as np
from scipy.fft import rfft, irfft
import scipy.signal as sg
# パラメータ
wav_name = "ATR_PM00.wav" # 読み込むWAVデータの名前
out_name = "soundout.wav" # 出力するWAVデータの名前
window = "hann" # 窓関数の種類
N = 1024 # FFT点数
r = 1.5 # スペクトル包絡の伸縮率
# WAVファイルを読み込む
x, fs = sf.read(wav_name)
# 短時間フーリエ変換(STFT)を行う X.shape=(n_bin, n_frame)
_, _, X = sg.stft(x, fs, window=window, nperseg=N)
X_phase = np.angle(X) # 観測信号の位相
n_bin = X.shape[0] # ビン数
n_frame = X.shape[1] # フレーム数
# 各numpy配列を準備
ceps_l = np.zeros(N) # 低次のケプストラム用の配列
ceps_h = np.zeros(N) # 高次のケプストラム用の配列
H_tilde = np.zeros(n_bin) # 伸縮後のスペクトル包絡用の配列
Y_abs = np.zeros(X.shape, dtype=np.float64) # 出力信号の振幅用の配列
eps = np.finfo(np.float64).eps # マシンイプシロン
# フレームごとにr培に伸縮したスペクトル包絡を求める
for i in range(n_frame):
spec_log = np.log(np.abs(X[:,i])+eps) # 対数変換
ceps = irfft(spec_log) # IFFTしてケプストラムを求める
lifter = 72 # 低次のケプストラムを72点まで抽出
ceps_l[0:lifter] = ceps[0:lifter] # 低次の抽出(前半)
ceps_l[N-lifter+1:] = ceps[N-lifter+1:] # 低次の抽出(後半)
ceps_h[lifter:N-lifter+1] = ceps[lifter:N-lifter+1] # 高次の抽出
H = np.real(rfft(ceps_l)) # FFTして実部だけ取り出す
G = np.real(rfft(ceps_h)) # FFTして実部だけ取り出す
# 対数スペクトル包絡をr倍に伸縮
for k in range(n_bin):
k2 = int(k/r)
alpha = k/r - k2
if k2 < n_bin-1:
H_tilde[k] = (1-alpha)*H[k2] + alpha*H[k2+1] # 線形補間
else: # k2がn_binを超えた場合
H_tilde[k] = np.log(eps) # -∞ に近いものを代入
Y_abs[:,i] = np.exp(H_tilde+G) # 振幅スペクトルを求める
# 位相と振幅でスペクトログラムを合成
Y = Y_abs * np.exp(X_phase)
# 逆短時間フーリエ変換(ISTFT)を行う
_, y = sg.istft(Y, fs=fs, window=window, nperseg=N)
# ファイルに書き込む
y = y/np.max(np.abs(y)) # ノーマライズ
sf.write(out_name, y, fs, subtype="PCM_16")
6~11行目:読みこむWAVデータ名、出力するデータ名、窓関数の種類、FFTの点数、スペクトル包絡の伸縮率などを指定しています。
16~20行目:短時間フーリエ変換をしています。また、観測信号の位相を取得しています。
31~38行目:フレームごとにケプストラム分析をして、対数スペクトル包絡 H を求めています。また、高次抽出をして微細構造 G も求めています。子音を発するときなどは、ケプストラムに基本周波数のピークがないので、低次抽出する点数は72点で固定しています。
39~46行目:対数スペクトル包絡を r 倍に伸縮しています。r<1.0 のときは k2(k') にスペクトル包絡がない場合があるので、そのときはとても大きいマイナスの数を代入しています。
47行目:対数スペクトル包絡 H と微細構造 G を足し合わせて、指数関数 exp で振幅スペクトルを求めています。
49~50行目:再合成した振幅と観測信号の位相を用いて、出力信号のスぺクトログラムを求めています。
処理結果
パラメータを以下のように設定してヘリウムボイスの変換を行いました。一応、r=0.5 としたときの処理結果についても載せました。音速が遅い気体を吸い込んだらおそらくr=0.5のときのような声になると思います。
| パラメータ名 | 変数名 | 設定値 |
|---|---|---|
| 窓関数 | window | ハン窓 |
| FFT点数 | N | 1024 |
| フレームシフト点数 | なし* | 512 |
| スペクトル包絡の伸縮率 | r | 1.5 or 0.5 |
* sg.stftのデフォルトのフレームシフト点数がFFT点数の半分のため、フレームシフト点数の変数は「なし」です。
ヘリウムボイスに変換した女性の音声が以下です。
女声の音声
女声の音声の処理結果(r=1.5)
女声の音声の処理結果(r=0.5)
信号処理によるノイズ(ミュージカルノイズ)はありますが、ヘリウムガスを吸い込んだときのような声になりました。r=0.5のときは、野太い人の声になってますね。
おわりに
本記事ではケプストラム分析を用いて音声をヘリウムボイスに変換しました。よくあるボイスチェンジャーがどのようなアルゴリズムになっているか理解できてよかったです。
■参考文献
[1] 川村新、”音声音響信号処理の基礎と実践”、コロナ社、2021.
■使用したデータについて
この記事で信号処理した音声はあみたろの声素材工房で提供されている音声を使用させていただきました。
【音声情報】
音声素材:あみたろの声素材工房 https://amitaro.net/
■変更履歴
・2025/01/30:タグの削除
