HPSSによる音源分離

音源分離・音源定位

調波打楽器音分離(HPSS:Harmonic/Percussive Sound Separation)を今回試してみました。HPSSはモノラル信号を打楽器音とそれ以外の音に分離する手法となります。

文献[1]がHPSSを最初に提案した論文だと思いますが、この記事では主に日本語でわかりやすい文献[2]を参考にします。

1 HPSSの概要
2 HPSSの手順
- 2.1 フローチャート
- 2.2 更新式の導出
3 HPSSの実装
4 HPSSの実験
5 おまけ：多重HPSSで歌声抽出
6 おわりに

HPSSの概要

音楽の中の成分はハーモニック成分とパーカッション成分に大きく分けられます。

ハーモニック成分はスペクトログラム上で時間軸方向にパワーが滑らかな成分であり、管楽器や擦弦楽器などに多く含まれます。例として、下図のエレキギターのスペクトログラムを見ると、時間軸方向にパワーが広がっているのがわかると思います。

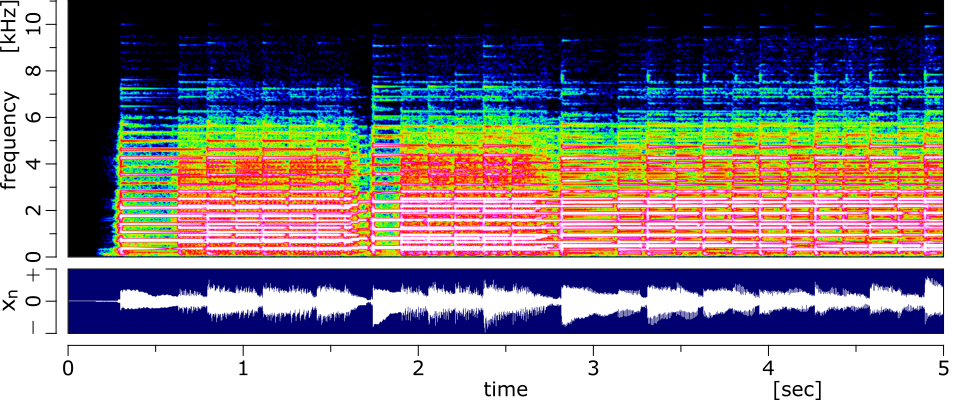
一方で、パーカッション成分は周波数軸方向にパワーが滑らかな成分であり、打楽器に多く含まれます。下図のスネアのスペクトログラムを見ると、周波数方向にパワーが広がっているのがわかると思います。

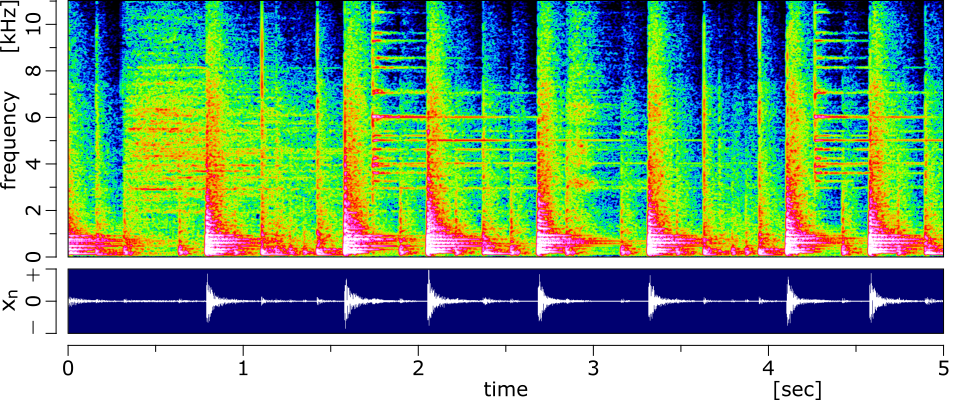
HPSS は楽器ごとにパワーの滑らかな方向が異なることを利用して、信号を下図のようにハーモニック成分とパーカッション成分に分離する手法となります。

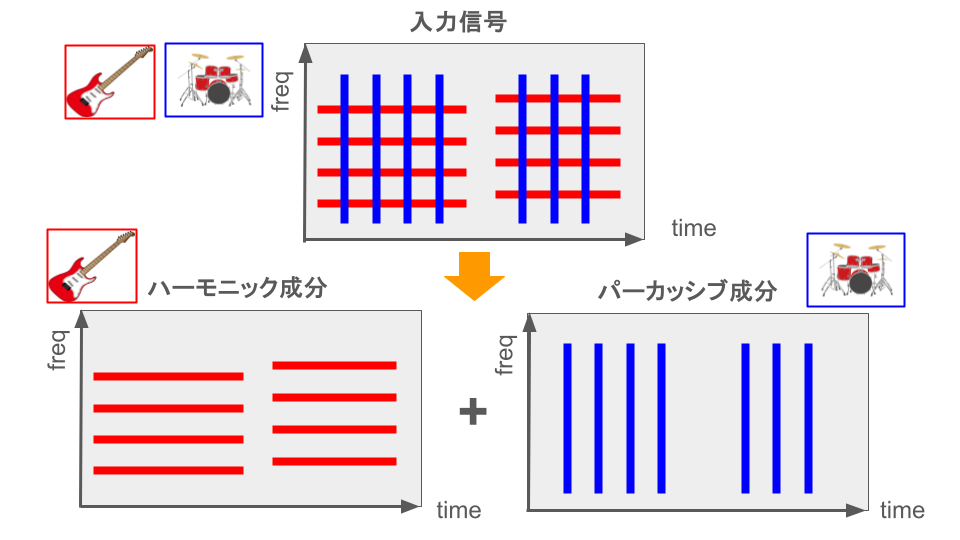
HPSSの手順

文献[2]のHPSSの手順について記載します。数式記号については文献[2]とは異なることに注意してください。

フローチャート

HPSSのフローチャートは下図のようになります。

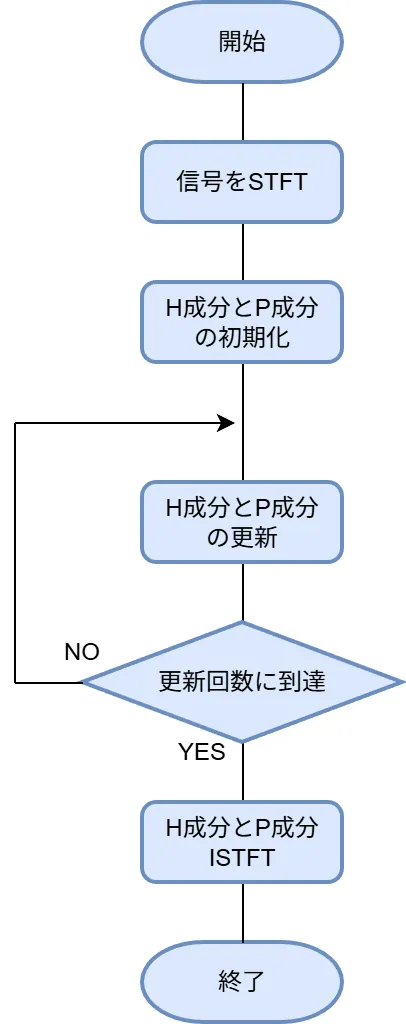
基本的にはH成分とP成分の更新を繰り返せばよいだけのシンプルな分離手法です。

H成分とP成分の更新式は以下となります。

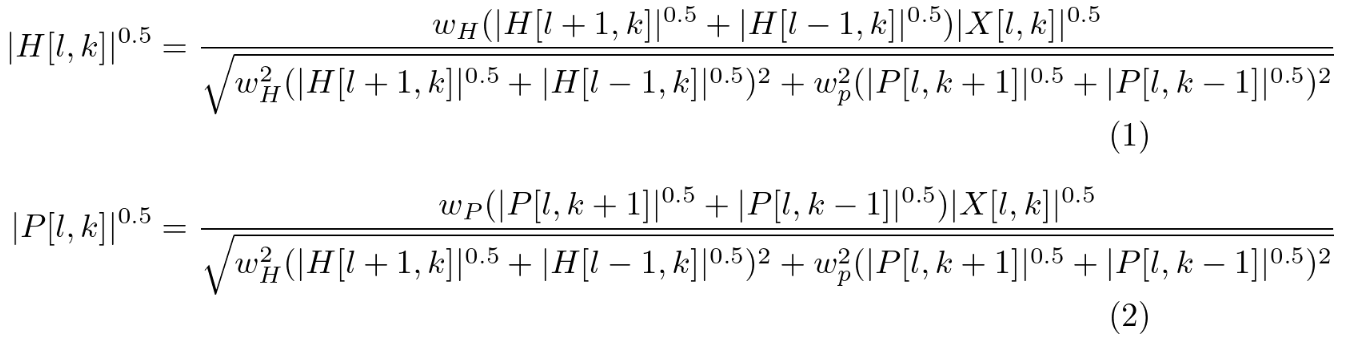
H成分とP成分の位相は入力信号と同じにします。各記号の意味は以下です。

更新式の導出

HPSSの更新式である(1)式と(2)式の導出を追っていきます。

目的関数と拘束条件

まず、以下の３つの指針

指針１：H成分は、スペクトログラム上において、時間軸方向に滑らかである。

指針２：P成分は、スペクトログラム上において、周波数方向に滑らかである。

指針３：H成分とP成分を足し合わせると、入力信号と等しくなる。

に基づいて目的関数を定義します[2]。

指針１,２を反映した目的関数 $\ J\ $が以下です。

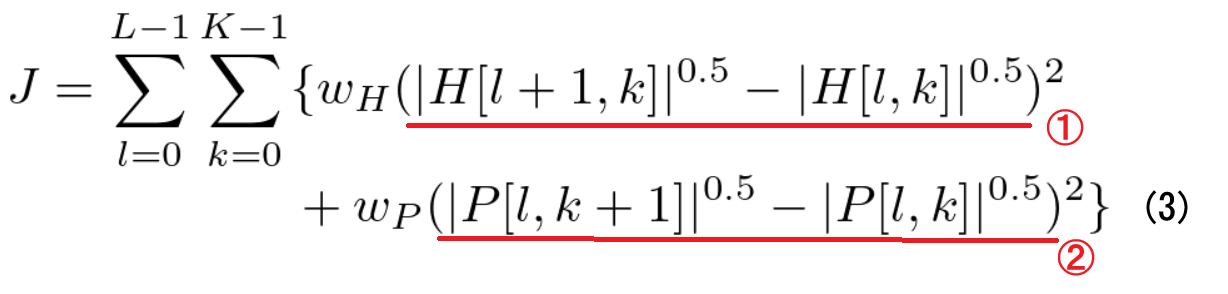
この目的関数を最小化することで、

①の時間軸方向の差分が小さくなり、H成分が時間軸方向に滑らかに
②の周波数方向の差分が小さくなり、P成分が周波数方向に滑らかに

なっていきます。

これに加えて、指針３を以下の式

$$
\begin{align}
|X[l,k]| = |H[l,k]|+|P[l,k]| \tag{4} \\[5pt] \angle X[l,k] = \angle H[l,k] = \angle P[l,k] \tag{5} \\[5pt] \end{align}
$$

で表し、これを拘束条件にします。

拘束条件の消去

拘束条件を満たしながら、目的関数を最小化するのは難しいため、ラグランジュの未定乗数法によって、拘束条件を消去します。

ラグランジュの未定乗数法から、新たな目的関数 $J'$は以下となります。

$$
\begin{equation}
J' = J-\sum_{l=0}^{L-1}\sum_{k=0}^{K-1} \lambda_{l,k}(|H[l,k]|+|P[l,k]|-|X[l,k]|) \tag{6}
\end{equation}
$$

$\lambda_{l,k}$ は未定乗数です。

目的関数の偏微分

$J'\ $に対する$\ |H[l,k]|^{0.5}, |P[l,k]|^{0.5}, \lambda_{l,k}\ $の偏微分を求めます。

最初に$\ J’\ $ではなく$\ J\ $に対する$\ |H[l,k]|^{0.5}$の偏微分を考えると、$|H[l,k]|^{0.5}\ $ 以外は定数とみなせる（$|H[l+1,k]|^{0.5}\ $とかも定数）ので、

$$
\begin{align}
J &\rightarrow \sum_{l=0}^{L-1}\sum_{k=0}^{K-1} w_{H}(|H[l+1,k]|^{0.5}-|H[l,k]|^{0.5})^{2} \\[5pt] &\rightarrow w_{H}(|H[l,k]|^{0.5}-|H[l-1,k]|^{0.5})^{2} \\[5pt] &\hspace{2em}+ w_{H}(|H[l+1,k]|^{0.5}-|H[l,k]|^{0.5})^{2} \tag{7}
\end{align}
$$

のように(7)式の$\ |H[l,k]|^{0.5}$の偏微分を求めればよくなる。よって、

$$
\begin{align}
\hspace{1.5em}\frac{\partial J}{\partial |H[l,k]|^{0.5}} &= 2w_{H}(|H[l,k]|^{0.5}-|H[l-1,k]|^{0.5}) \\[1pt] &\hspace{1em} -2w_{H}(|H[l+1,k]|^{0.5}-|H[l,k]|^{0.5}) \\[8pt] &= 4w_{H}|H[l,k]|^{0.5} \\[6pt] &\hspace{1em} -2w_{H}(|H[l+1,k]|^{0.5}+|H[l-1,k]|^{0.5}) \tag{8}
\end{align}
$$

(6)式の第２項についても同じように偏微分すると、$\ J'\ $に対する$\ |H[l,k]|^{0.5}$の偏微分は

$$
\begin{align}
\frac{\partial J’}{\partial |H[l,k]|^{0.5}} &= \frac{\partial J}{\partial |H[l,k]|^{0.5}}
- 2\lambda_{l,k}|H[l,k]|^{0.5} \\[5pt] &= 2(2w_{H}-\lambda_{l,k})|H[l,k]|^{0.5} \\[5pt] &\hspace{1em} -2w_{H}(|H[l+1,k]|^{0.5}+|H[l-1,k]|^{0.5}) \tag{9}
\end{align}
$$

同様に$\ J'\ $に対する$\ |P[l,k]|^{0.5}$の偏微分は

$$
\begin{align}
\frac{\partial J’}{\partial |P[l,k]|^{0.5}} &= 2(2w_{P}-\lambda_{l,k})|P[l,k]|^{0.5} \\
&\hspace{1em} -2w_{P}(|P[l,k+1]|^{0.5}+|P[l,k-1]|^{0.5}) \tag{10}
\end{align}
$$

$\ J'\ $に対する$\ \lambda_{l,k}\ $の偏微分は

$$
\begin{equation}
\frac{\partial J’}{\partial \lambda_{l,k}} = |X[l,k]|-|H[l,k]|-|P[l,k]| \tag{11}
\end{equation}
$$

更新式の導出

(9)式、(10)式、(11)式から、

$$
\begin{align}
&\frac{\partial J’}{\partial |H[l,k]|^{0.5}}=0, \\[8pt] &\frac{\partial J’}{\partial |P[l,k]|^{0.5}}=0, \\[8pt] &\hspace{1em} \frac{\partial J’}{\partial \lambda_{l,k}}=0 \\
\tag{12}
\end{align}
$$

を満たす $|H[l,k]|,\ |P[l,k]|,\ \lambda_{l,k}$を求める。(9)式と(10)式と(12)式から

$$
\begin{align}
|H[l,k]|^{0.5} &= w_{H}\frac{(|H[l+1,k]|^{0.5}+|H[l-1,k]|^{0.5})}{2w_{H}-\lambda_{l,k}} \tag{13} \\[5pt] |P[l,k]|^{0.5} &= w_{P}\frac{(|P[l,k+1]|^{0.5}+|P[l,k-1]|^{0.5})}{2w_{P}-\lambda_{l,k}} \tag{14} \\[5pt] \end{align}
$$

(13)式と(14)式を(11)式に代入して、$w_{H}\approx w_{P}\approx 1 $と仮定すると、

$$
\begin{align}
0=&|X[l,k]|-|H[l,k]|-|P[l,k]| \\[5pt] \approx&|X[l,k]|-w_{H}^{2}\frac{(|H[l+1,k]|^{0.5}+|H[l-1,k]|^{0.5})^{2}}{(2-\lambda_{l,k})^{2}} \\[5pt] &-w_{P}^{2}\frac{(|P[l,k+1]|^{0.5}+|P[l,k-1]|^{0.5})^{2}}{(2-\lambda_{l,k})^{2}} \tag{15}
\end{align}
$$

(15)式をさらに変形すると

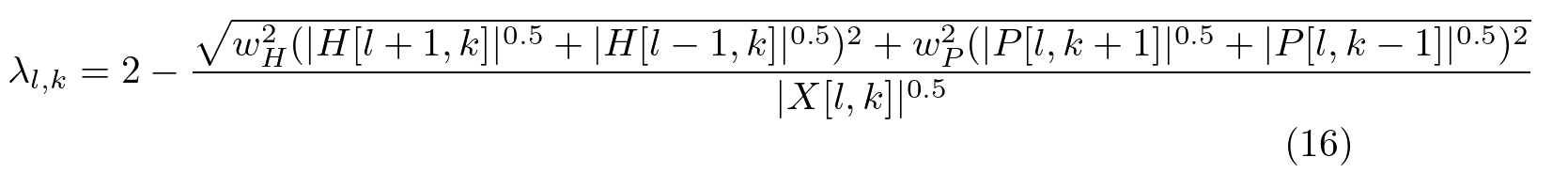
(16)式を(13)式と(14)式に代入することで

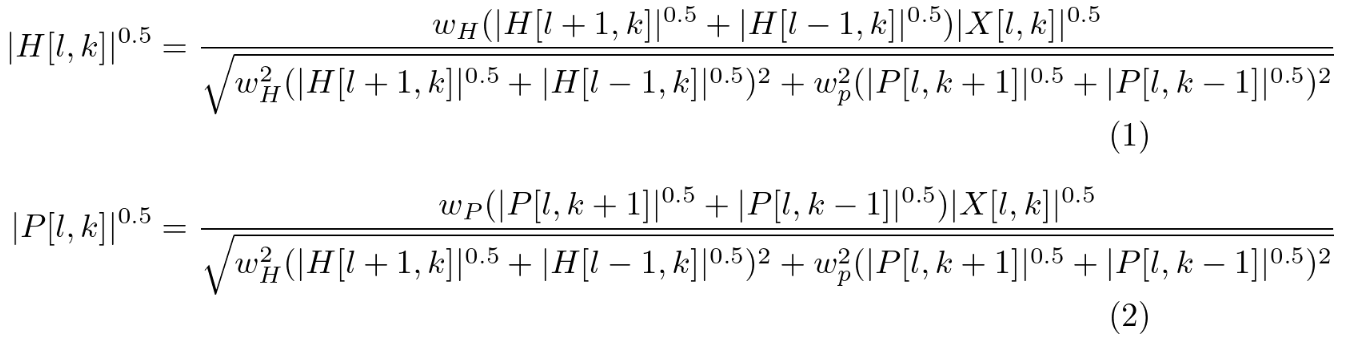
となり、(1)式と(2)式が導出されます。右辺にはまだ変数が含まれており、2LK元1次連立方程式となりますが、これを陽に解くことは困難なため、各右辺を評価した式を逐次的に左辺に代入することで、HPSSの近似解を得ます。

HPSSの実装

HPSSをPythonで実装しました。Pythonのソースコード hpss.py は以下となります。

import numpy as np
import resampy
import soundfile as sf
import scipy.signal as sg

# 次の２の累乗を計算
def next_power_of_two(n):
    if n <= 0:
        return 1
    return 1 << (n - 1).bit_length()

def hpss(x, win, N_fft, fs):
    # STFT
    SFT = sg.ShortTimeFFT(win, hop=N_fft//2, fs=fs)
    X_stft = SFT.stft(x)
    H_stft = np.zeros_like(X_stft)
    P_stft = np.zeros_like(X_stft)

    # H成分、P成分の初期化
    H_abs = np.zeros(X_stft.shape, dtype=np.float64)
    P_abs = np.zeros(X_stft.shape, dtype=np.float64)
    H_abs = np.sqrt(0.5 * np.abs(X_stft))
    P_abs = np.sqrt(0.5 * np.abs(X_stft))

    # 変数初期化
    bin_n = H_abs.shape[0]
    time_n = H_abs.shape[1]
    H_abs = np.insert(H_abs, 0, 0.0, axis=1)
    H_abs = np.insert(H_abs, time_n+1, 0.0, axis=1)
    H_tmp = np.zeros(X_stft.shape, dtype=np.float64)
    P_tmp = np.zeros(X_stft.shape, dtype=np.float64)
    X_abs = np.zeros(X_stft.shape, dtype=np.float64)

    # HPSS
    for i in range(iteration):

        # 更新式の準備
        # |H[l+1,k]|^(0.5) + |H[l-1,k]|^(0.5)
        H_tmp[:,:] = H_abs[:,0:time_n] + H_abs[:,2:time_n+2]

        # |P[l,k+1]|^(0.5) + |P[l,k-1]|^(0.5)
        P_tmp[1:bin_n-1,:] = P_abs[0:bin_n-2,:] + P_abs[2:bin_n,:]
        P_tmp[0,:] = P_abs[0,:]               # k=0 そのまま
        P_tmp[bin_n-1,:] = P_abs[bin_n-1,:]   # k=K-1 そのまま

        # |W[l,k]|^(0.5)
        X_abs[:,:] = H_abs[:,1:time_n+1]**2 + P_abs[:,:]**2
        X_abs[:,:] = np.sqrt(X_abs)

        # H成分更新
        H_abs[:,1:time_n+1] = w_H*H_tmp[:,:]*X_abs[:,:]
        H_abs[:,1:time_n+1] = H_abs[:,1:time_n+1]/np.sqrt((w_H**2)*H_tmp[:,:]**2+(w_P**2)*P_tmp[:,:]**2)

        # P成分更新
        P_abs[:,:] = w_P*P_tmp[:,:]*X_abs[:,:]
        P_abs[:,:] = P_abs[:,:]/np.sqrt((w_H**2)*H_tmp[:,:]**2+(w_P**2)*P_tmp[:,:]**2)

    H_abs[:,1:time_n+1] = H_abs[:,1:time_n+1]**2
    P_abs = P_abs**2

    H_stft = X_stft * H_abs[:,1:time_n+1]/(H_abs[:,1:time_n+1]+P_abs)
    P_stft = X_stft * P_abs/(H_abs[:,1:time_n+1]+P_abs)

    # 逆短時間フーリエ変換
    h = SFT.istft(H_stft, k1=length_x)
    p = SFT.istft(P_stft, k1=length_x)

    return h, p

# parameter
iteration = 50     # 繰り返し回数
w_H = 0.95         # ハーモニック成分重み
w_P = 1.00         # パーカッシブ成分重み
fs_new = 16000     # サンプリングレート
frame_length = 0.03 # フレームの長さ [s]

# WAVファイルを読み込む
x, fs = sf.read('sample1/input.wav')

# リサンブリング
if fs != fs_new: 
    x = resampy.resample(x, sr_orig=fs, sr_new=fs_new)

# FFT点数
length_x = len(x)                    # xのデータ長
N_fft = int(fs_new * frame_length)   # FFT点数
N_fft = next_power_of_two(N_fft)     # FFT点数を2の累乗にする

# 窓関数作成
win = sg.windows.hann(N_fft)  # ハン窓作成

# 短時間フーリエ変換
h, p = hpss(x, win, N_fft, fs_new)

# WAV書き込む
sf.write("sample1/harmonic.wav", h, fs_new, subtype="PCM_24")
sf.write("sample1/percussive.wav", p, fs_new, subtype="PCM_24")

● 短時間フーリエ変換(STFT)

    # STFT
    SFT = sg.ShortTimeFFT(win, hop=N_fft//2, fs=fs)
    X_stft = SFT.stft(x)
    H_stft = np.zeros_like(X_stft)
    P_stft = np.zeros_like(X_stft)

13行目～17行目でSTFTを行ってます。フレームシフト量はフレーム幅の半分となってます。

● H成分とP成分の初期化

    # H成分、P成分の初期化
    H_abs = np.zeros(X_stft.shape, dtype=np.float64)
    P_abs = np.zeros(X_stft.shape, dtype=np.float64)
    H_abs = np.sqrt(0.5 * np.abs(X_stft))
    P_abs = np.sqrt(0.5 * np.abs(X_stft))

H成分とP成分の絶対値の初期値は入力信号の半分としています。

● 変数の初期化

    # 変数初期化
    bin_n = H_abs.shape[0]
    time_n = H_abs.shape[1]
    H_abs = np.insert(H_abs, 0, 0.0, axis=1)
    H_abs = np.insert(H_abs, time_n+1, 0.0, axis=1)
    H_tmp = np.zeros(X_stft.shape, dtype=np.float64)
    P_tmp = np.zeros(X_stft.shape, dtype=np.float64)
    X_abs = np.zeros(X_stft.shape, dtype=np.float64)

28行目と29行目でH成分のスペクトログラムの時間軸の両端に一列ずつ付け足して、両端も更新できるようにします。周波数軸の両端（Fs=0Hzとナイキスト周波数）は処理しないので追加しないです。

● H成分とP成分の更新

        # H成分更新
        H_abs[:,1:time_n+1] = w_H*H_tmp[:,:]*X_abs[:,:]
        H_abs[:,1:time_n+1] = H_abs[:,1:time_n+1]/np.sqrt((w_H**2)*H_tmp[:,:]**2+(w_P**2)*P_tmp[:,:]**2)

        # P成分更新
        P_abs[:,:] = w_P*P_tmp[:,:]*X_abs[:,:]
        P_abs[:,:] = P_abs[:,:]/np.sqrt((w_H**2)*H_tmp[:,:]**2+(w_P**2)*P_tmp[:,:]**2)

あらかじめ37行目～48行目で計算できるところを求めて、50行目～56行目でH成分とP成分を更新します。

● 最終的なH成分とP成分

    H_stft = X_stft * H_abs[:,1:time_n+1]/(H_abs[:,1:time_n+1]+P_abs)
    P_stft = X_stft * P_abs/(H_abs[:,1:time_n+1]+P_abs)

入力にH成分とP成分の絶対値から求めたマスクを掛けて、最終的なH成分とP成分を求める。

● 逆短時間フーリエ変換(ISTFT)

    # 逆短時間フーリエ変換
    h = SFT.istft(H_stft, k1=length_x)
    p = SFT.istft(P_stft, k1=length_x)

ISTFTを行います。出力が元の入力信号の長さと同じになるように k1 に入力信号の長さを入れます。

HPSSの実験

以下のパラメータでジャズをHPSSで音源分離してみました。

表：HPSSのパラメータ
パラメータ名	変数名	設定値
サンプリングレート	fs_new	16 kHz
フレーム長	frame_length	0.03 秒
更新回数	iteration	50 回
窓関数	win	ハン窓
H成分の重み	w_H	0.95
P成分の重み	w_P	1.00

分離結果は以下となります。

入力音（ジャズ）

ハーモニック成分

パーカッシブ成分

せとち

おー、H成分のWAVでは打楽器の音が抑制されていますね。逆にP成分のWAVでは調波音を持つ楽器音が抑制されてます。

スペクトログラムでは以下のようになっています。

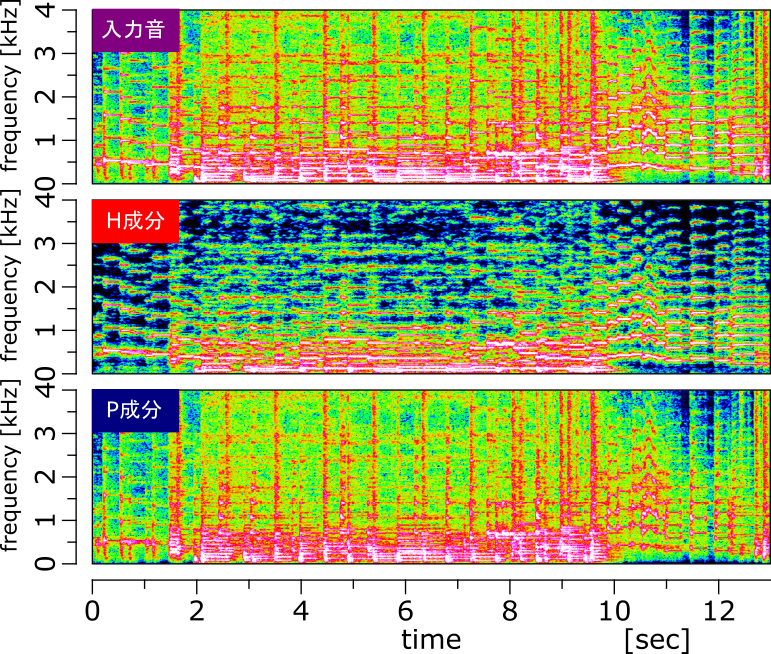
スペクトログラムから見ても、P成分の出力に時間軸方向の成分が多く含まれるのを確認できます。ただ、ピアノやトランペットのアタック部分がP成分に含まれてしまっているので、アタック部分の対策は必要だなと感じます。

おまけ：多重HPSSで歌声抽出

文献[2]では多重HPSSによる歌声抽出を実装していたので、それも紹介しておきます。

歌声についてはSTFTのフレームサイズによってHPSSで H成分・P成分のどちらになるかが異なります。

歌声は 5～8Hz のスペクトル揺らぎがあるため、フレームサイズを 200ms くらいにすれば、周波数分解能が 5Hz になり、揺らぎを識別でき、P成分として判定されやすくなります。

一方で、フレームサイズが 30ms くらいの場合、周波数分解能が 33Hz になり、周波数方向の揺らぎが観測できず、H成分として判定されやすくなります。

このことを利用して、HPSSを2回使って歌声を以下のように抽出します。

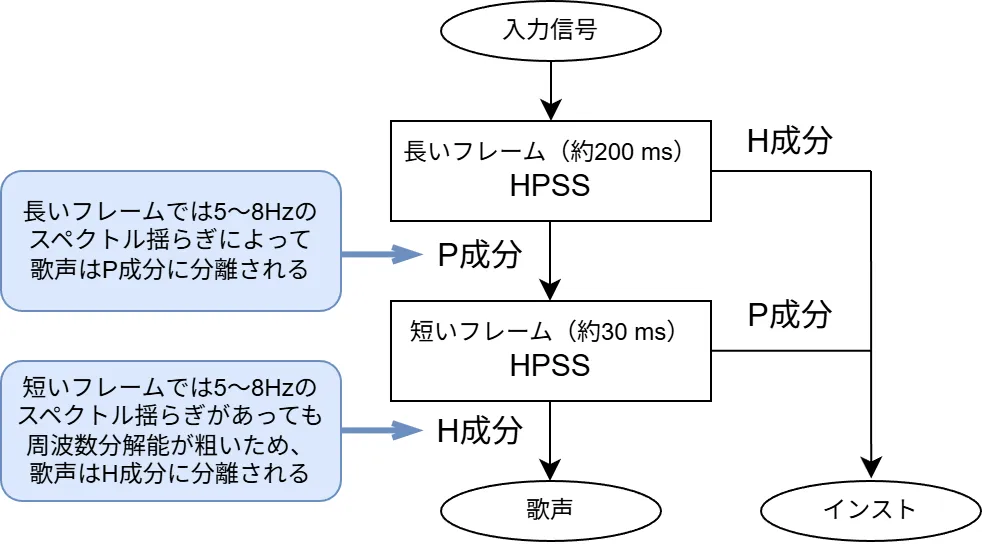
一回目に長いフレームのHPSSを使用して、調波音をもつ楽器をH成分として分離します。2回目に短いフレームのHPSSを使用して、打楽器をP成分として分離して、歌声を抽出するという流れとなります。

多重HPSSを使用した歌声抽出のソースコードは以下です。

多重HPSSソースコード（クリックで展開）

import numpy as np
import resampy
import soundfile as sf
import scipy.signal as sg

# 次の２の累乗を計算
def next_power_of_two(n):
    if n <= 0:
        return 1
    return 1 << (n - 1).bit_length()

def hpss(x, w_H, w_P, win, N_fft, fs):
    # STFT
    SFT = sg.ShortTimeFFT(win, hop=N_fft//2, fs=fs)
    X_stft = SFT.stft(x)
    H_stft = np.zeros_like(X_stft)
    P_stft = np.zeros_like(X_stft)

    # H成分、P成分の初期化
    H_abs = np.zeros(X_stft.shape, dtype=np.float64)
    P_abs = np.zeros(X_stft.shape, dtype=np.float64)
    H_abs = np.sqrt(0.5 * np.abs(X_stft))
    P_abs = np.sqrt(0.5 * np.abs(X_stft))

    # 変数初期化
    bin_n = H_abs.shape[0]
    time_n = H_abs.shape[1]
    H_abs = np.insert(H_abs, 0, 0.0, axis=1)
    H_abs = np.insert(H_abs, time_n+1, 0.0, axis=1)
    H_tmp = np.zeros(X_stft.shape, dtype=np.float64)
    P_tmp = np.zeros(X_stft.shape, dtype=np.float64)
    W_abs = np.zeros(X_stft.shape, dtype=np.float64)

    # HPSS
    for i in range(iteration):

        # 更新式の準備
        # |H[l+1,k]|^(0.5) + |H[l-1,k]|^(0.5)
        H_tmp[:,:] = H_abs[:,0:time_n] + H_abs[:,2:time_n+2]

        # |P[l,k+1]|^(0.5) + |P[l,k-1]|^(0.5)
        P_tmp[1:bin_n-1,:] = P_abs[0:bin_n-2,:] + P_abs[2:bin_n,:]
        P_tmp[0,:] = P_abs[0,:]               # k=0 そのまま
        P_tmp[bin_n-1,:] = P_abs[bin_n-1,:]   # k=K-1 そのまま

        # |W[l,k]|^(0.5)
        W_abs[:,:] = H_abs[:,1:time_n+1]**2 + P_abs[:,:]**2
        W_abs[:,:] = np.sqrt(W_abs)

        # H成分更新
        H_abs[:,1:time_n+1] = w_H*H_tmp[:,:]*W_abs[:,:]
        H_abs[:,1:time_n+1] = H_abs[:,1:time_n+1]/np.sqrt((w_H**2)*H_tmp[:,:]**2+(w_P**2)*P_tmp[:,:]**2)

        # P成分更新
        P_abs[:,:] = w_P*P_tmp[:,:]*W_abs[:,:]
        P_abs[:,:] = P_abs[:,:]/np.sqrt((w_H**2)*H_tmp[:,:]**2+(w_P**2)*P_tmp[:,:]**2)

    H_abs[:,1:time_n+1] = H_abs[:,1:time_n+1]**2
    P_abs = P_abs**2

    H_stft = X_stft * H_abs[:,1:time_n+1]/(H_abs[:,1:time_n+1]+P_abs)
    P_stft = X_stft * P_abs/(H_abs[:,1:time_n+1]+P_abs)

    # 逆短時間フーリエ変換
    h = SFT.istft(H_stft, k1=length_x)
    p = SFT.istft(P_stft, k1=length_x)

    return h, p

# parameter
iteration = 50     # 繰り返し回数
w_Hl = 1.00        # ハーモニック成分重み
w_Pl = 0.95        # パーカッシブ成分重み
w_Hs = 0.95        # ハーモニック成分重み
w_Ps = 1.00        # パーカッシブ成分重み
fs_new = 16000     # サンプリングレート
frame_length_short = 0.03 # フレームの長さ 短い [s]
frame_length_long = 0.20 # フレームの長さ 長い [s]

# WAVファイルを読み込む
x, fs = sf.read('input.wav')

# リサンブリング
if fs != fs_new: 
    x = resampy.resample(x, sr_orig=fs, sr_new=fs_new)

# FFT点数
length_x = len(x)  # xのデータ長
N_fft_long = int(fs_new * frame_length_long)    # FFT点数
N_fft_long = next_power_of_two(N_fft_long)      # FFT点数を2の累乗にする
N_fft_short = int(fs_new * frame_length_short)  # FFT点数
N_fft_short = next_power_of_two(N_fft_short)    # FFT点数を2の累乗にする
print(N_fft_long)
print(N_fft_short)

# 窓関数作成
win_long = sg.windows.hann(N_fft_long)    # ハン窓作成
win_short = sg.windows.hann(N_fft_short)  # ハン窓作成

# 短時間フーリエ変換
h_long, p_long = hpss(x, w_Hl, w_Pl, win_long, N_fft_long, fs_new)
h_short, p_short = hpss(p_long, w_Hs, w_Ps, win_short, N_fft_short, fs_new)

# 歌声抽出
inst  = h_long + p_short
vocal = h_short

# WAV書き込む
sf.write("vocal.wav", vocal, fs_new, subtype="PCM_24")
sf.write("inst.wav", inst, fs_new, subtype="PCM_24")

パラメータを以下のように設定して多重HPSSで歌声抽出しました。

表：HPSSのパラメータ
パラメータ名	変数名	設定値
サンプリングレート	fs_new	16 kHz
長いフレーム長	frame_length_long	0.2 秒
短いフレーム長	frame_length_short	0.03 秒
更新回数	iteration	50 回
窓関数	win	ハン窓
H成分の重み(長いフレーム)	w_Hl	1.00
P成分の重み(長いフレーム)	w_Pl	0.95
H成分の重み(短いフレーム)	w_Hs	0.95
P成分の重み(短いフレーム)	w_Ps	1.00

分離結果は以下となります。

入力音声

歌声

インスト

たしかに歌声の抽出結果においてはインストが抑制され、インストでは歌声が抑制されてますね。ただ、インストの中にまだ歌声が残っていたり、抽出した歌声の発音が聞き取りづらかったりで、多重HPSSに課題は多そうという印象です。

おわりに

本記事では、HPSSで音源分離を試してみました。シンプルな方法で音源分離できてすごく面白いなと思いました。

ただし、各楽器のアタック部分がP成分の出力に含まれてしまうので、やはりそこに課題があるなと感じます。

■参考文献
[1] N. Ono, K. Miyamoto, J. Le Roux, H. Kameoka and S. Sagayama, "Separation of a Monaural Audio Signal into Harmonic/Percussive Components by Complementary Diffusion on Spectrogram," 2008 16th European Signal Processing Conference, Lausanne, Switzerland, 2008, pp. 1-4.
[2] 橘秀幸, 小野順貴, 嵯峨山茂樹, “スペクトルの時間変化に基づく音楽音響信号からの歌声成分の強調と抑圧,” 情報処理学会研究報告, vol. 2009-MUS-81(12), pp. 1-6, 2009.

■使用した楽曲について
この記事で使用した楽曲は Pixabay で提供されているものを使用させていただきました。

Music: "Jazz Music Free" by PulseBox — Pixabay
https://pixabay.com/ja/music/伝統的なジャズ-jazz-no-copyright-440559/

Music: "Tera Pyar Mera Junoon" by Greenz-Music — Pixabay
https://pixabay.com/music/pop-tera-pyar-mera-junoon-334753/