周波数領域 ICA を使用した音源分離

周波数領域における独立成分分析(frequency domain ICA: FDICA)を使用した音源分離を試してみました。

独立成分分析のやり方は前回の記事（独立成分分析による音源分離）で紹介しましたが、今回は周波数領域における独立成分分析のやり方となります。

参考文献[1]がすでに完成された説明となっているため、その内容をほとんどなぞるだけですが、FDICAについて説明していきたいと思います。

注意点としまして、参考文献[1]と記号の表記が異なることに気をつけてください。

1 FDICA の問題設定
2 最尤推定によるICA
3 FDICAの問題
4 プログラム
- 4.1 ソースコード
- 4.2 実行方法
5 シミュレーション実験
- 5.1 方法
- 5.2 音源分離の結果
6 おわりに

FDICA の問題設定

短時間フーリエ変換（STFT）した観測信号$\ {\boldsymbol X}[l,k]\ $は以下のように表せると考えます。

$$
{\boldsymbol X}[l,k] = {\boldsymbol A}[k] {\boldsymbol S}[l,k] \tag{1}
$$

表現を変えると以下です。

$$
\begin{equation}
\begin{bmatrix}
X_{1}[l,k] \\
\vdots \\
X_{m}[l,k] \\
\vdots \\
X_{M}[l,k] \end{bmatrix}
= {\boldsymbol A}[k] \begin{bmatrix}
S_{1}[l,k] \\
\vdots \\
S_{i}[l,k] \\
\vdots \\
S_{I}[l,k] \end{bmatrix} \tag{2}
\end{equation}
$$

ここで、$\ m\ $は観測信号の番号、$\ i\ $は音源信号の番号、$\ l\ $はフレーム番号、$\ k\ $は周波数ビン番号、$\ {\boldsymbol A}[k]\ $は M x I の混合行列、$\ S_{i}[l,k]\ $はSTFT後の音源信号です。

また、マイクの数$\ M\ $と音源数$\ I\ $は等しいと仮定します。

FDICA では、混合行列$\ {\boldsymbol A}[k]\ $の逆行列である$\ {\boldsymbol W}[k]\ $を推定することで、音源を分離していきます。

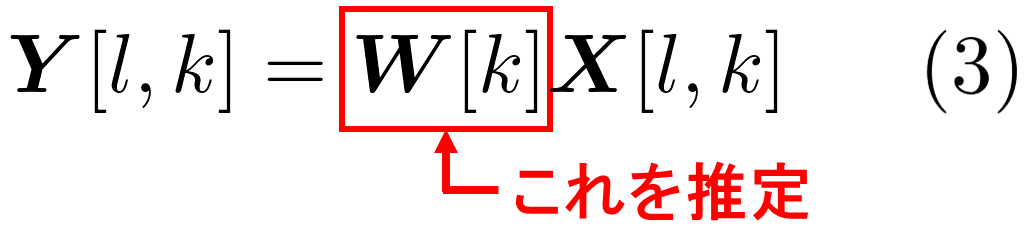
このとき、${\boldsymbol X}[l,k]\ $以外は未知として、信号の到来方向もわからないものとします。

最尤推定によるICA

前回の記事（独立成分分析による音源分離）では非ガウス性（尖度）を最大化することで各音源信号が独立となるように分離しました。実は独立成分分析にはこの他にもいろいろなやり方があります。

今回は各音源信号が独立であると仮定したとき、観測信号の尤度が最大となるように分離行列を決定していきます。今回は信号が複素数であることに注意してください。

尤度の導出

まず、音源信号が統計的に独立であると仮定した場合、分離信号の確率密度関数は以下のように表現できます。

$$
p({\boldsymbol Y}[l,k]) = \prod_{i=1}^{I} p(Y_{i}[l,k]) \tag{4}
$$

また、線形変換時の確率密度関数は以下のように表せます。

$$
p({\boldsymbol X}[l,k]) = |{\rm det} {\boldsymbol W}[k]|^2 p({\boldsymbol Y}[l,k]) \tag{5}
$$

(4)式、(5)式から、観測信号の確率密度関数は以下のように表せます。

$$
p({\boldsymbol X}[l,k]) = |{\rm det} {\boldsymbol W}[k]|^2 \prod_{i=1}^{I} p(Y_{i}[l,k]) \tag{6}
$$

また、分離行列を

$$
{\boldsymbol W}[k] = [{\boldsymbol w}_{1}^{*}[k] \cdots {\boldsymbol w}_{i}^{*}[k] \cdots {\boldsymbol w}_{I}^{*}[k] ]^T \tag{7}
$$

のように表せば（$\ \cdot^{*}$は複素共役）、観測信号の確率密度関数は以下のように表せます。

$$
p({\boldsymbol X}[l,k]) = |{\rm det} {\boldsymbol W}[k]|^2 \prod_{i=1}^{I} p({\boldsymbol w}_{i}^{H} {\boldsymbol X}[l,k]) \tag{8}
$$

このとき、尤度関数$\ \mathcal{L}\ $は以下のように表せます。

$$
\begin{align}
\mathcal{L}({\boldsymbol W}[k]) &= \prod_{l=1}^{L} p({\boldsymbol X}[l,k]) \\
&= \prod_{l=1}^{L} \prod_{i=1}^{I} \left\{p({\boldsymbol w}_{i}^{H} {\boldsymbol X}[l,k])\right\} \hspace{2pt} |{\rm det} {\boldsymbol W}[k]|^2 \tag{9}
\end{align}
$$

尤度関数よりも対数尤度関数のほうが取り扱いが簡単なため、対数尤度関数を求めると以下の式になります。

$$
\log{\mathcal{L}({\boldsymbol W}[k])} = \sum_{l=1}^{L} \sum_{i=1}^{I} \log{p({\boldsymbol w}_{i}^{H} {\boldsymbol X}[l,k])} + 2L\log{|{\rm det} {\boldsymbol W}[k]|} \tag{10}
$$

(10)式が最大となるように分離行列を決めればよいのですが、一般的には(10)式に(-1/L)を掛けた(11)式を最小化する場合が多いです。

$$
{\rm minimize} \hspace{1em} \frac{1}{L}\sum_{l=1}^{L} \sum_{i=1}^{I} -\log{p({\boldsymbol w}_{i}^{H} {\boldsymbol X}[l,k])} - 2\log{|{\rm det} {\boldsymbol W}[k]|} \tag{11}
$$

また、以下の音源信号の負の対数尤度関数はコントラスト関数と呼ばれています。

$$
G(Y_{i}[l,k]) = -\log{p(Y_{i}[l,k]={\boldsymbol w}_{i}^{H}{\boldsymbol X}[l,k])} \tag{12}
$$

(12)式を使用すると(11)式は以下のように表せます。

$$
{\rm minimize} \hspace{1em} \frac{1}{L}\sum_{l=1}^{L} \sum_{i=1}^{I} G(Y_{i}[l,k]) - 2\log{|{\rm det} {\boldsymbol W}[k]|} \tag{13}
$$

パラメータの最適化

(13)式を最小化するために勾配法を用いると分離行列の更新式は以下のようになります。

$$
\begin{align}
{\boldsymbol W}^{(t+1)}[k] &= {\boldsymbol W}^{(t)}[k] - \mu \cfrac{\partial \frac{1}{L}\sum_{l=1}^{L} \sum_{i=1}^{I} G(Y_{i}[l,k]) - 2\log{|{\rm det} {\boldsymbol W}[k]|}}{\partial {\boldsymbol W}^{*}[k]} \\
&= {\boldsymbol W}^{(t)}[k] - \mu \left(\frac{1}{L}\sum_{l=1}^{L} \phi({\boldsymbol Y}[l,k]){\boldsymbol X^{H}}[l,k] - ({\boldsymbol W^{H}}[k])^{-1}\right) \tag{14}
\end{align}
$$

$$
\begin{equation}
\phi({\boldsymbol Y}[l,k])
=
\begin{bmatrix}
\phi(Y_{1}[l,k]) \\
\vdots \\
\phi(Y_{i}[l,k]) \\
\vdots \\
\phi(Y_{I}[l,k])
\end{bmatrix} \tag{15}
\end{equation}
$$

$$
\begin{equation}
\phi(Y_{i}[l,k]) = \frac{\partial G(Y_{i}[l,k])}{\partial Y_{i}^{*}[l,k]} \tag{16}
\end{equation}
$$

ここで、$t$ は繰り返し計算の繰り返し回数のインデックス、$\mu$ は学習係数です。

勾配法の場合、(14)式のように逆行列の計算が必要となってしまうので、少しメンドクサイです。

そのため、自然勾配法がよく使われています。自然勾配法では勾配に右から${\boldsymbol W^{H}}[k]{\boldsymbol W}[k]$ をかけたものを新たな勾配として用います。それを新たな勾配として用いてよいのかという疑問があるかと思いますが、筆者もわかりません！今度調べたいと思います。

自然勾配法では更新式は以下となります。

$$
{\boldsymbol W}^{(t+1)}[k] = {\boldsymbol W}^{(t)}[k] + \mu \left({\boldsymbol I} - \frac{1}{L}\sum_{l=1}^{L} \phi({\boldsymbol Y}[l,k]){\boldsymbol Y^{H}}[l,k] \right) {\boldsymbol W}^{(t)}[k] \tag{17}
$$

(14)式の導出：(14)式の導出を記載いたしました。内容に誤りがある場合はご指摘をお願いいたします。

まず、以下を導出する。

$$
\cfrac{\partial}{\partial {\boldsymbol W}^{*}[k]} 2\log{|{\rm det}{\boldsymbol W}[k]|} = ({\boldsymbol W^{H}}[k])^{-1}
$$

上記の式は以下のように導出できる。

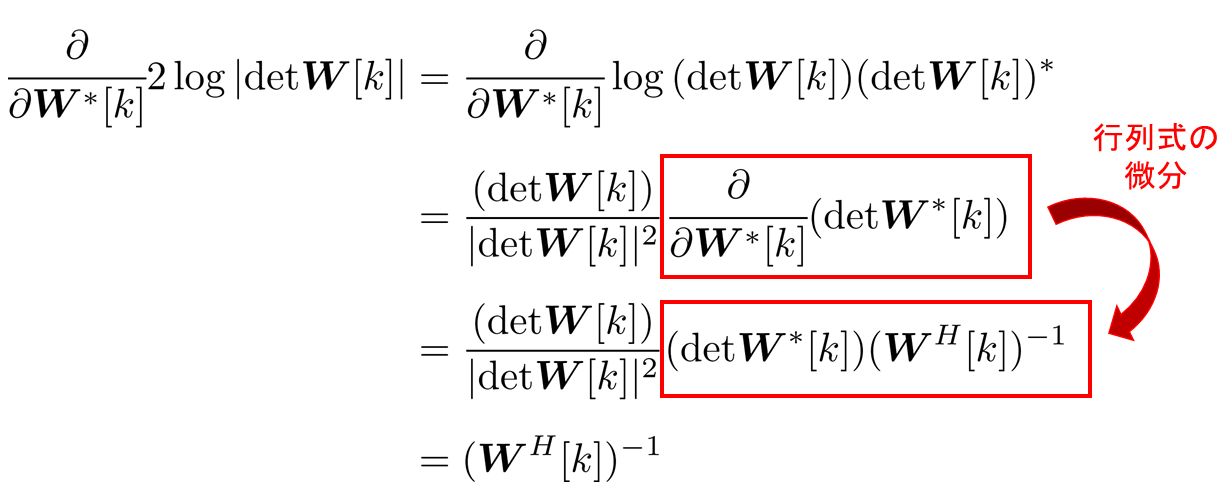
次に、以下を導出する。

$$
\cfrac{\partial}{\partial {\boldsymbol W}^{*}[k]} \sum_{i=1}^{I} G(Y_{i}[l,k]) = \phi({\boldsymbol Y}[l,k]){\boldsymbol X^{H}}[l,k] $$

行列の微分を行うと以下のようになります。

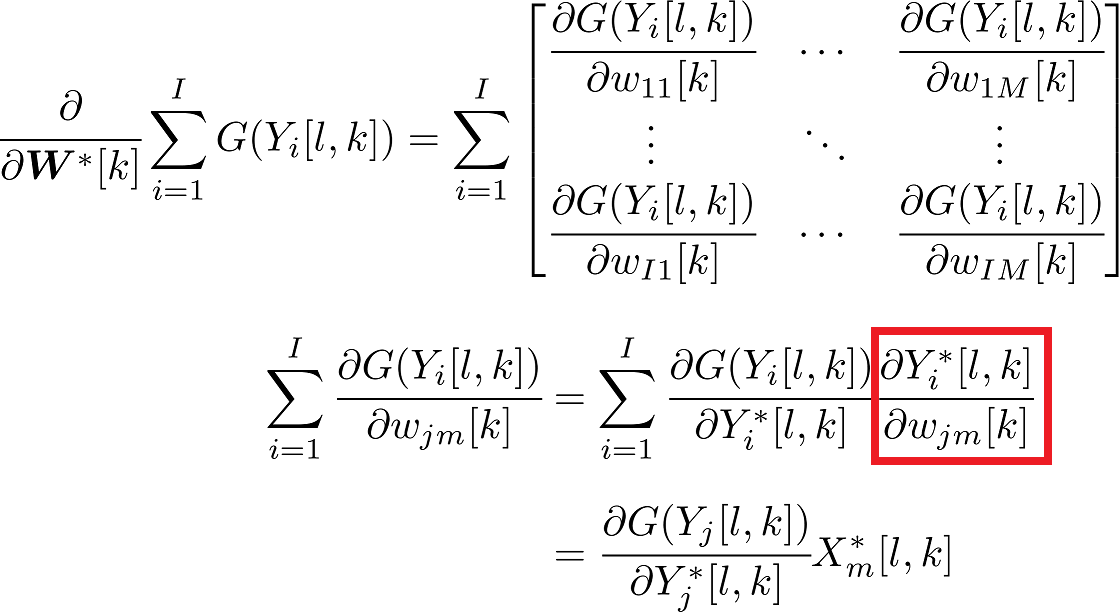
ここで上記の赤い四角の計算は以下のようにしました。

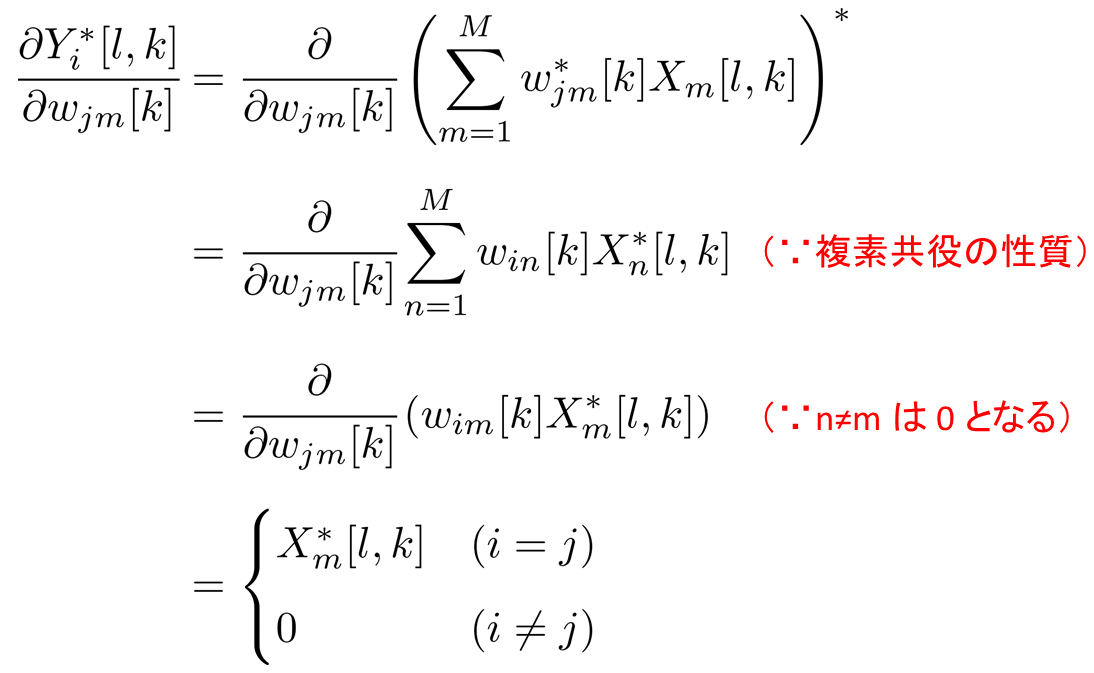
したがって、

音源モデル

(17)式を分離行列が収束するまで繰り返し計算すれば分離行列が求められます。ただ、$\phi({\boldsymbol Y}[l,k])$ がこのままではわからず計算できないです。

$\phi({\boldsymbol Y}[l,k])$ を計算するために、$p(Y_{i}[l,k])$の分布を仮定していきます。この仮定する分布を音源モデルと呼びます。

今回は音声を分離するため、音源モデルとしてラプラス分布を使用したいと思います。

音源モデルをラプラス分布とした場合、 $p(Y_{i}[l,k])\ $は以下の式となります。

$$
p(Y_{i}[l,k]) = \alpha \exp{\left(-\frac{|Y_{i}[l,k]|}{b}\right)} \tag{18}
$$

$\alpha$は定数、$b$は尺度母数です。

分布の形状についてはガウス分布と比較してラプラス分布は以下のようになります。

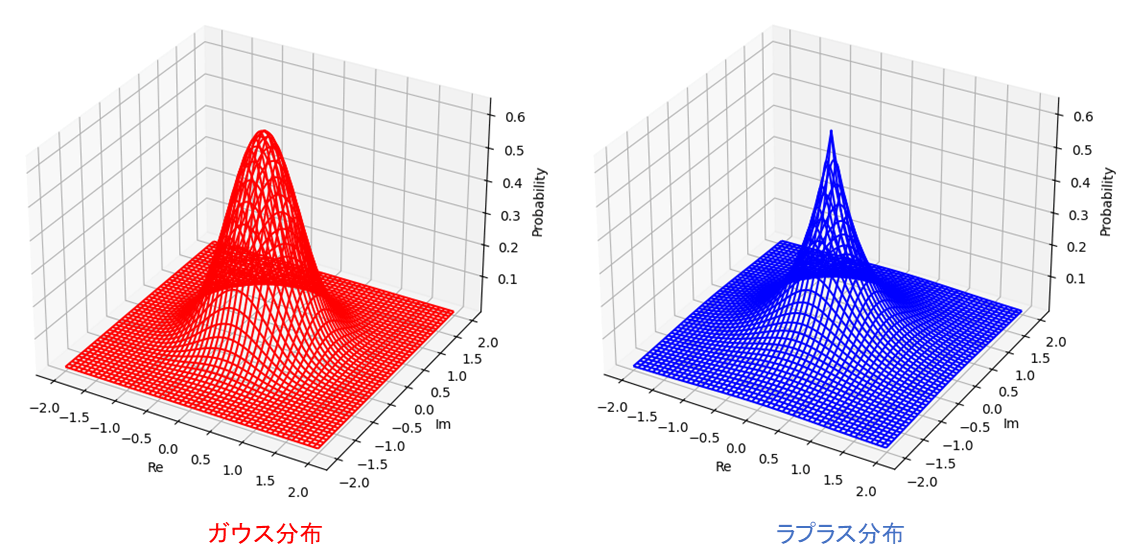
音源モデルをラプラス分布としたとき、以下のようになります。

$$
\begin{align}
\phi(Y_{i}[l,k]) = &\frac{\partial G(Y_{i}[l,k])}{\partial Y_{i}^{*}[l,k]} \\[5pt] = &\frac{\partial}{\partial Y_{i}^{*}[l,k]} \left(-\log{\alpha \exp{\left(-\frac{|Y_{i}[l,k]|}{b}\right)}} \right) \\[5pt] = &\frac{\partial}{\partial Y_{i}^{*}[l,k]} \left(-\log{(\alpha)} + \frac{|Y_{i}[l,k]|}{b}\right) \\[5pt] = &\frac{1}{b}\frac{\partial}{\partial Y_{i}^{*}[l,k]} |Y_{i}[l,k]| \\[5pt] = &\frac{1}{2b}\frac{Y_{i}[l,k]}{|Y_{i}[l,k]|}　\\[5pt] = &\frac{Y_{i}[l,k]}{|Y_{i}[l,k]|} \hspace{1em} (b=1/2)\tag{19}
\end{align}
$$

$b\ $ については信号の大きさに影響するパラメータですが、後に説明する音量の不定性の問題で信号の大きさを調節するため、値はなんでもよいです。計算しやすいように$\ b=1/2\ $ とします。

これで、(17)式が計算できます。

FDICAの問題

以上で周波数ごとの分離行列が求まったため、これで終わりかと思いきや、FDICAでは次に説明するICAの２つの不確定性の問題があるため、それを解決する必要があります。

周波数間パーミュテーション問題

ICAでは以下の図のように出力された分離信号の順番がわからないという問題があります。

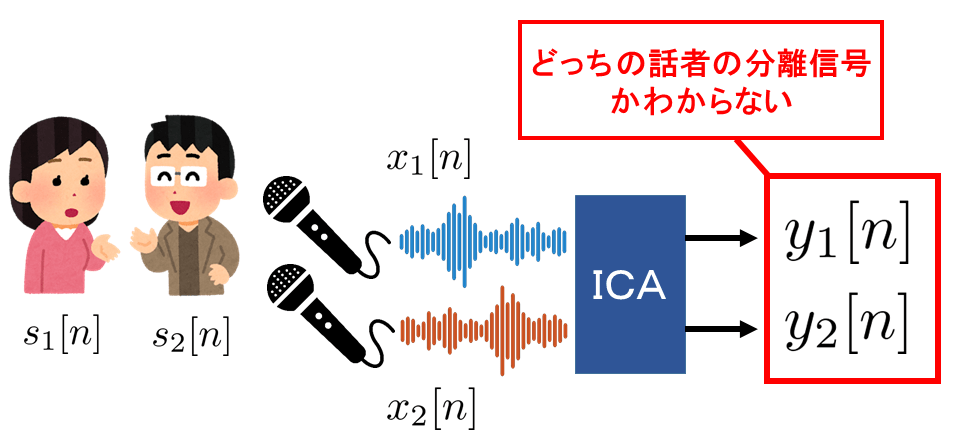
STFTを使わない場合、分離結果を聞き分ければ良いだけですが、FDICAの場合、周波数ごとのICAの結果を組み合わせるため問題となってきます。

このままだと周波数ごとに音源が異なる出力音声となるため、処理前よりもひどい音になりかねません。

出力信号の音量の不定性の問題

また、ICAでは以下の図のように出力された分離信号の音量がわからないという問題があります。

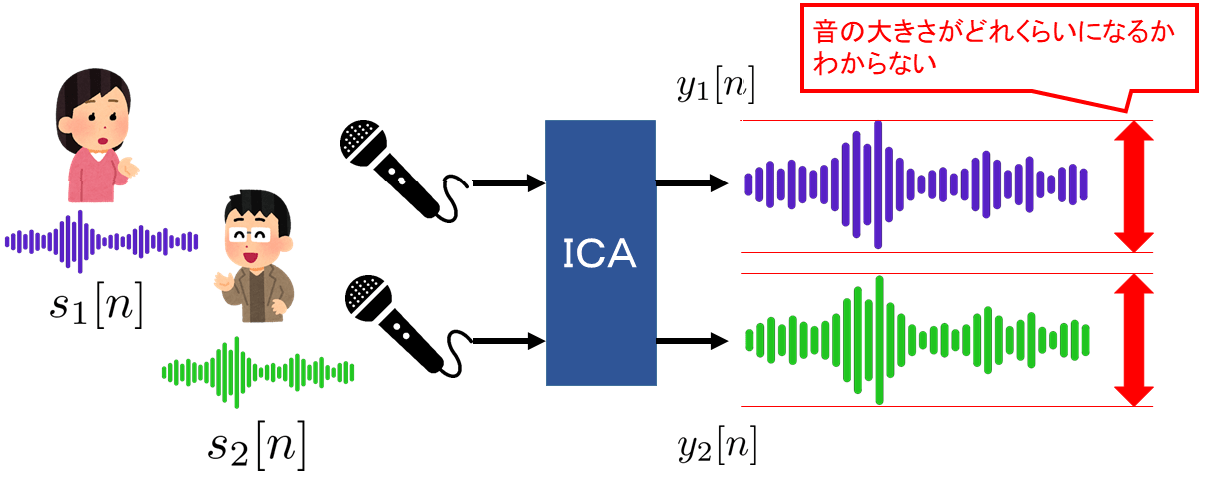
これもFDICAの場合、ある周波数ではエネルギーが大きくて、違う周波数では小さくなるということが起きてしまいます。

また、周波数ごとの音の大きさが異なる場合、音色がかわってしまうため、変な音声となってしまう可能性があります。

周波数間パーミュテーション解決策

周波数間パーミュテーション問題の解決策はいくつかあるようですが、ここでは文献[1]で紹介されている音量の時間パターンの類似性を使用した方法を紹介したいと思います。

手順は以下となります。

分離信号の大きさを正規化する
正規化した分離信号の大きさを用いて、音源間の相関から分離精度が良い周波数の順番を求める
分離精度が良い周波数の順に、周波数間の相関が高くなるように音源の順番を並べ替える

分離信号の大きさを正規化

まず、以下の式で分離信号の大きさを正規化します。

$$
Z_{i}[l,k] = \cfrac{|Y_{i}[l,k]|}{\sum_{j=1}^{I}|Y_{j}[l,k]|} \tag{20}
$$

$(l, k)$ における分離信号の大きさの比のようなものかなと解釈しています。

音源間の相関から分離精度を求める

次に周波数ごとに$Z_{i}[l,k]$の音源間の相関$\ C[k]\ $を以下のように計算します。

$$
C[k] = \sum_{l=1}^{L}\sum_{i=1}^{I}\sum_{j=1}^{I} Z_{i}[l,k]Z_{j}[l,k]\tag{21}
$$

この相関が高いほど分離信号どうしが似ているということなので、分離がうまくいっていないということになります。

この指標を用いて、分離精度の良い周波数の順を求めていきます。

周波数間の相関から音源の順番を並べ替え

分離精度が良い順に音源の順番を並べ替えていきます。

$C[k]$ が$\ n$ 番目に小さい周波数ビン番号を $k^{(n)}$ として、基準の振幅スペクトルパターンを以下とします。

$$
A_{i}[l] = Z_{i}[l,k^{(1)}] \tag{22}
$$

それから、次に分離精度がよい周波数ビン番号$\ k^{(2)}\ $との相関

$$
\sum_{l=1}^{L}\sum_{i=1}^{I} A_{i}[l] Z_{i}[l,k^{(2)}] \tag{23}
$$

が最大となるように周波数ビン番号$\ k^{(2)}\ $における分離信号の順番を並べ替えます。

同じ音源の周波数成分どうしであれば、下図のように音量の変化の仕方も類似するはずですので上記の相関が高くなるいうことです。

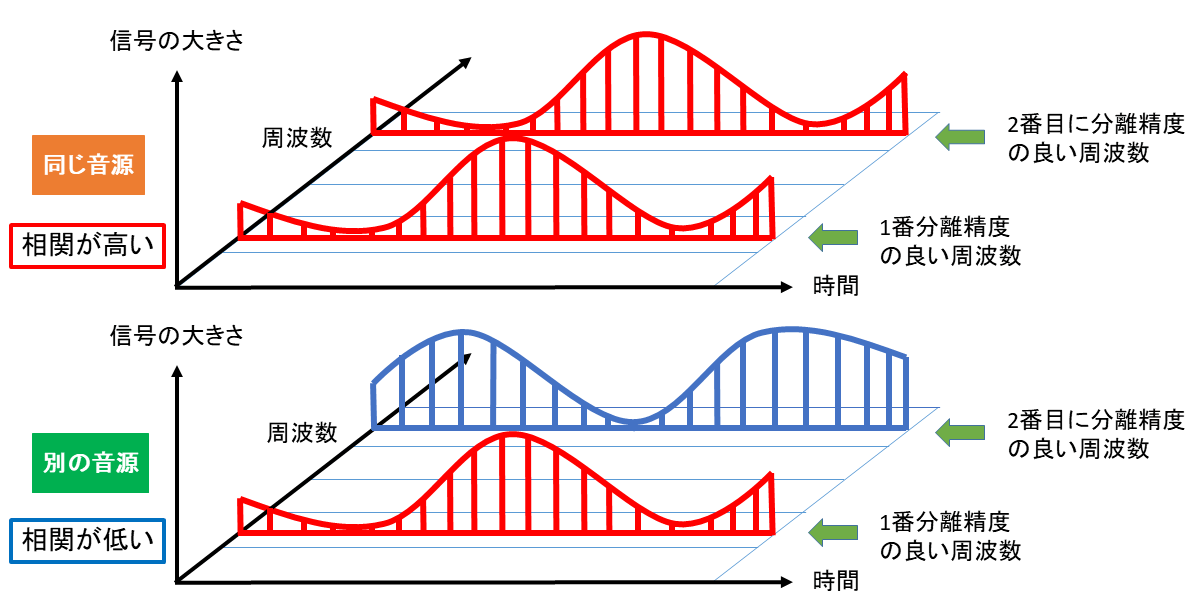
逆に違う音源であれば、音量の変化の仕方が異なり相関が低くなるはずです。

周波数ビン番号$\ k^{(2)}\ $における分離信号の順番を並べ替えたら、基準の振幅スペクトルパターンを以下の式で更新いたします。

$$
A_{i}[l] \leftarrow A_{i}[l] + Z_{p(i)}[l,k^{(2)}] \tag{24}
$$

ここで、$p(i)$ は並べ替え後の分離信号の順番です。上記の処理を $n=3,4,\cdots $ と繰り返していき、最終的に全ての周波数の分離信号の順番を並べ替えます。

出力信号の音量の不定性の解決策

音量の不定性の問題の解決策についてはプロジェクションバックという方法があります。

プロジェクションバックは図のように特定の観測信号に含まれる音源の大きさに戻す方法となります（$\ a_{11}, a_{12}\ $は混合行列$\boldsymbol{A}$の要素）。

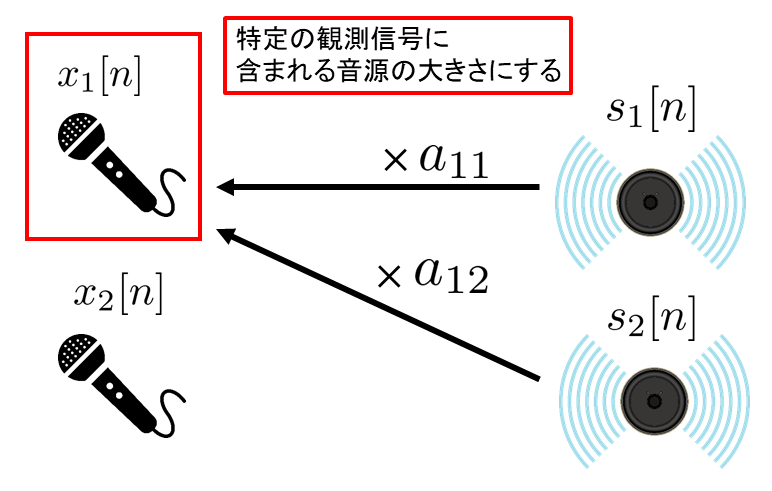
混合行列$\boldsymbol{A}$ については推定した分離行列の逆行列を計算することで求めます。

$m$番目の観測信号を使用したプロジェクションバックの場合、数式で表現すると以下となります。

$$
Y'_{i}[l,k] = a_{mi}[k] Y_{i}[l,k] \tag{25}
$$

以上がFDICAの手順となります。

プログラム

FDICAのプログラムをPythonで書いてみました。

ソースコード

結構長いですが、FDICAで音源分離するソースコード fdica.py は以下です。ほとんど参考文献[1]のソースコードのマネですが…。

import soundfile as sf
import numpy as np
import scipy.signal as sg
import itertools as itertools

# パラメータ
n_fft   = 512       # 窓の大きさ
hop     = n_fft//2  # フレームシフトサイズ
window  = "hann"    # 窓の種類
mu      = 0.1       # 学習係数
n_mic   = 3         # 観測信号の数
n_iter  = 200       # 繰り返し計算回数
mic_dir = "mic/"    # 録音データがあるディレクトリ
out_dir = "out/"    # 出力データを格納するディレクトリ

#############################################
# パーミュテーション問題解決のための並べ替え
# Y_stft: 分離信号(STFT) (n_mic, n_K, n_L)
#############################################
def solve_permutation_problem( Y_stft ):

    # 分離信号の大きさの正規化
    Y_stft_abs = np.abs( Y_stft )
    Y_stft_abs_sum = np.sum( Y_stft_abs, axis=0, keepdims=True )
    Z = Y_stft_abs / np.maximum( Y_stft_abs_sum, 1.e-18 )

    # 音源間の相関から分離精度を求める
    C = np.einsum('ikl,jkl->k', Z, Z)
    freq_order = np.argsort( C )

    # 周波数間の相関から音源の順番を並べ替え
    ## 取りうる順列の作成
    permutations = list(itertools.permutations(range(n_mic)))
    perm_result = {}
    is_first = True
    #permutations = [(0, 1, 2), (0, 2, 1), … (2, 1, 0)]

    ## 分離精度が良い周波数から並べ替え
    for freq in freq_order:

        if is_first==True:
            is_first=False
            A = Z[:,freq_order[0],:]
            perm_result[freq] = range(n_mic) 

        else:
            ### 相関が最大となる順番を探索
            max_corr = 0
            max_corr_perm = None
            for perm in permutations:

                #### 相関を求める 
                Z_k_temp = Z[list(perm),freq,:]
                corr = np.sum( A * Z_k_temp )

                #### 初期設定
                if max_corr_perm is None:
                    max_corr = corr
                    max_corr_perm = list(perm)                
                #### 相関が最大ならば
                elif corr > max_corr:
                    max_corr = corr
                    max_corr_perm = list(perm)

            ### 音源の順番を並べ替える
            perm_result[freq] = max_corr_perm

            ### 振幅スペクトルパターンの更新
            A += Z[max_corr_perm,freq,:]

    return perm_result    

#############################################
# プロジェクションバックの関数
# Y_stft: 分離信号(STFT) (n_mic, n_K, n_L)
# W: 分離行列 (n_K, n_mic, n_mic)
#############################################
def projection_back( Y_stft, W ):

    # 推定した分離行列から混合行列を求める
    A = np.linalg.pinv( W )

    # 0番目のマイクの音源の大きさに合わせる
    Y_dash_stft = np.einsum('ki,ikl->ikl', A[:,0,:], Y_stft)

    return Y_dash_stft

# WAVファイル名のリスト作成
wav_list = []
for i in range( n_mic ):
    wav_list.append( "mic" + str(i) + ".wav" )

# WAVファイルを読み込む
for i, wav_name in enumerate( wav_list ):
    x_tmp, fs = sf.read( mic_dir + wav_name )
    if i==0:
        x=np.zeros((n_mic, len(x_tmp)))
        x[0,:] = x_tmp 
    else:
        x[i,:] = x_tmp

# 窓関数の作成
w_func = sg.get_window( window, n_fft )

# 短時間フーリエ変換(STFT)
SFT = sg.ShortTimeFFT(win=w_func, hop=hop, fs=fs)
X_stft = SFT.stft(x)

# 初期化
_, n_K, n_L = X_stft.shape
W = np.zeros((n_K, n_mic, n_mic), dtype=complex)
W = W + np.eye(n_mic,n_mic)[None,:,:]

# 繰り返し分離行列を更新
for t in range( n_iter ):

    # 音源分離信号を得る
    Y_stft = np.einsum('kim,mkl->ikl', W, X_stft)

    # コントラスト関数を計算
    G = 2 * np.abs(Y_stft)

    # コスト計算
    cost = np.sum(np.mean(G,axis=-1))-np.sum(2*np.log(np.abs(np.linalg.det(W))))
    print(cost)

    # コントラスト関数の微分
    phi = Y_stft/np.maximum(np.abs(Y_stft), 1.e-18)

    # 勾配を計算
    I = np.eye(n_mic,n_mic)
    phi_s = np.einsum('ikl,jkl->klij', phi, np.conjugate(Y_stft))
    phi_s = np.mean(phi_s, axis=1)

    deltaW = np.einsum('kij,kjm->kim', I[None,:,:]-phi_s, W)

    # 分離行列を更新
    W = W + mu*deltaW

# 出力信号を分離
Y_stft = np.einsum('kim,mkl->ikl', W, X_stft)

# パーミュテーションを解く
perm_result = solve_permutation_problem( Y_stft )

# プロジェクションバック
Y_stft = projection_back( Y_stft, W )

# 音源の並び順を変える
for k in range(n_K):
    Y_stft[:,k,:]=Y_stft[perm_result[k],k,:]

# 逆短時間フーリエ変換
y = SFT.istft( Y_stft, k1=x.shape[1] )

# WAVファイルを書き込む
for i in range( n_mic ):
    wav_out_name = out_dir + "out" + str(i) + ".wav"
    sf.write( wav_out_name, y[i,:], fs, subtype='PCM_16' )

実行方法

(1) プログラムを実行するディレクトリに以下を用意する。

ソースコード(fdica.py)
複数の入力 WAV データを格納するディレクトリ
出力WAVデータを格納するディレクトリ

(2) ソースコード6～14行目のパラメータを修正する。

# パラメータ
n_fft   = 512       # 窓の大きさ
hop     = n_fft//2  # フレームシフトサイズ
window  = "hann"    # 窓の種類
mu      = 0.1       # 学習係数
n_mic   = 3         # 観測信号の数
n_iter  = 200       # 繰り返し計算回数
mic_dir = "mic/"    # 録音データがあるディレクトリ
out_dir = "out/"    # 出力データを格納するディレクトリ

(3) 以下のコマンドで python を実行することで、音源分離のデータが指定したディレクトリに格納される。

$ python fdica.py

シミュレーション実験

室内音響シミュレーションで作成した混合音をFDICAで音源分離してみました。

方法

室内音響シミュレーションにはPythonのライブラリであるPyRoomAcousticsを用いました。

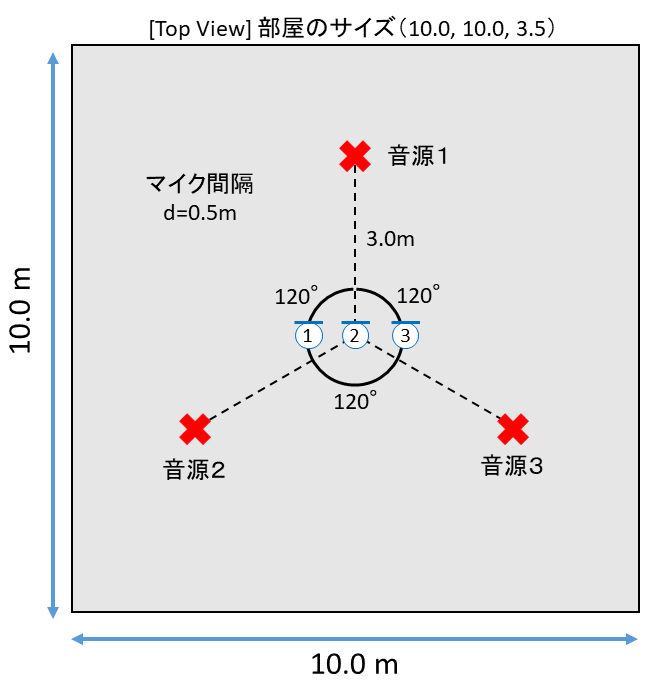
シミュレーション上で図のように音源とマイクを配置して、3個のマイクで音声データを録音しました。

以下をクリックするとシミュレーションに用いたソースコードが展開されます。

room_sim.py（クリックで展開）

import numpy as np
import pyroomacoustics as pra
import soundfile as sf
from librosa import resample

fs = 16000  # リサンプリング後の周波数 
rt60_tgt = 0.2    # 残響時間
room_size = [10, 10, 3.5]  # 部屋の大きさ(x, y, z)
SNR = 90          # SN比
dir_src = "src/"  # 音源のフォルダ
dir_mic = "mic/"  # 録音したデータのフォルダ
src_list = ["sound1.wav", "sound2.wav", "sound3.wav"]

# 音源とマイクの位置を決定
center = [5.0, 5.0]  # 中心の位置 
n_src  = 3     # 音源の数
phi0   = 90    # 一個目の音源の方向 [度]
radius = 3     # 音源の中心からの距離 [m]
n_mic  = 3     # マイクの数
d      = 0.5   # マイクの間隔 [m]
pos_z  = 1.25  # マイクと音源のz軸上の位置

# 音源を円状アレイで配置
phi0 = np.radians( phi0 ) # deg -> rad 変換
s_locs = pra.circular_2D_array(center, n_src, phi0, radius)
s_locs = np.insert(s_locs, 2, pos_z, axis=0) # z軸追加
print(s_locs)

# マイクを線状アレイで配置
m_locs = pra.linear_2D_array(center, n_mic, 0, d)
m_locs = np.insert(m_locs, 2, pos_z, axis=0) # z軸追加
print(m_locs)

# WAVファイルを読み込む
audio = []
for i, src_name in enumerate(src_list):
    x, fs_tmp = sf.read(dir_src+src_name)
    x = resample(x, orig_sr=fs_tmp, target_sr=fs)
    audio.append(x)
audio = np.array(audio)

# 残響時間と部屋の大きさから吸音率と反射回数を決定
e_absorption, max_order = pra.inverse_sabine(rt60_tgt, room_size)

# 部屋の作成
room = pra.ShoeBox(
    room_size, fs=fs, materials=pra.Material(e_absorption), max_order=max_order
)

# 部屋に音源を配置
for i in range(n_src):
    room.add_source(s_locs[:,i], signal=audio[i,:], delay=0)

# 部屋にマイクを配置
room.add_microphone_array(
    pra.MicrophoneArray(m_locs, fs=fs)
)

# シミュレーションする
room.simulate(snr=SNR)

# マイクで録音した音を書き出す
mic_data = room.mic_array.signals
mic_data = mic_data/np.max(np.abs(mic_data)) # ノーマライズ
for i in range(n_mic):
    name = dir_mic+"mic"+str(i)+".wav"
    sf.write(name, mic_data[i,:], fs, subtype='PCM_16')

録音された音源は以下となります。

観測信号 x1

観測信号 x2

観測信号 x3

何も聴きとれないですね。

音源分離の結果

FDICAで音源分離した結果は以下のようになりました。

分離信号 y1

分離信号 y2

分離信号 y3

せとち

ちょっと他の音声も混ざっていますが、結構分離できてますね。やはり残響があると音源分離の難易度が上がってきます。

おわりに

過去一長くなりましたが、本記事では FDICA について記載いたしました。

正直なハナシ、参考文献[1]については私が学生のころに読んで、その説明のわかりやすさに驚きました。それでも、ところどころ式変形がわからなかったりして、理解を深めるのに苦労した覚えがあります。いまでも何故そうなるのかわからない部分は多くありますが（例えば(5)式や(17)式）、理解できた箇所につきましては皆さんに共有したいと思い、この記事を執筆致しました。

学生の頃の私と同じように苦労している方に参考文献[1]の補助として見てもらえれば幸いです。

参考文献
[1] 戸上真人, ”Python で学ぶ音源分離機械学習実践シリーズ”, 株式会社インプレス, 2020．

Pythonで学ぶ音源分離機械学習実践シリーズ

¥3,850 （2024/10/26 22:46時点 | Amazon調べ）

Amazon

楽天市場

Yahooショッピング

メルカリ

ポチップ

■使用した音声について
この記事で使用した音声は Mozilla Foundation で提供されている音声を使用させていただきました。

【音声のページ】
・ "Common Voice: A Massively-Multilingual Speech Corpus" 2020 Mozilla Foundation (Licensed under CC-0) https://huggingface.co/datasets/mozilla-foundation/common_voice_14_0