
音に広がりを持たせるコーラスとフランジャーを実装しました。
コーラスは合唱のように微妙にずれた音を作り出すエフェクターです。一方でフランジャーはジェットサウンドと呼ばれるジェット機のような音を作りだすエフェクターとなります。
コーラスとフランジャーは違うエフェクターとしてありますが、原理は全く同じであり、パラメータの値が違うだけのため一緒に紹介します。
実装方法
コーラス・フランジャーは以下のようにビブラートによってずれた音と原音を足し合わせることで実装できます[1]。
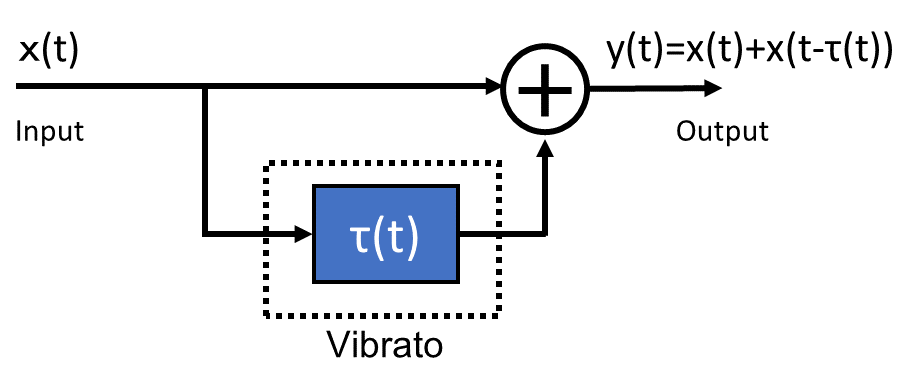
遅延は以下のようにします。
$$
\tau(t) = d+depth\sin(2\pi r t)
$$
ここで、depth はビブラートの深さ(DEPTH)、r はビブラートの周波数(RATE)を表す。d は平均遅延時間です。
デジタルで処理する場合は遅延を以下のようにします。
$$
\tau[n] = F_s \left(d + depth \sin\left(2\pi r \frac{n}{F_s}\right)\right)
$$
コーラスとフランジャーの差異
コーラスとフランジャーの違いはパラメータの値だけとなります。
参考文献[2]によれば、フランジャーでは d とdepth を小さく設定(約2ms)して、コーラスでは大きく設定(約20ms)するみたいです。また、r についてはフランジャーでは高めに設定します。
d=0.025[s]、depth=0.010[s]、r=0.1[Hz]に設定したコーラスの周波数特性は以下のようになります。
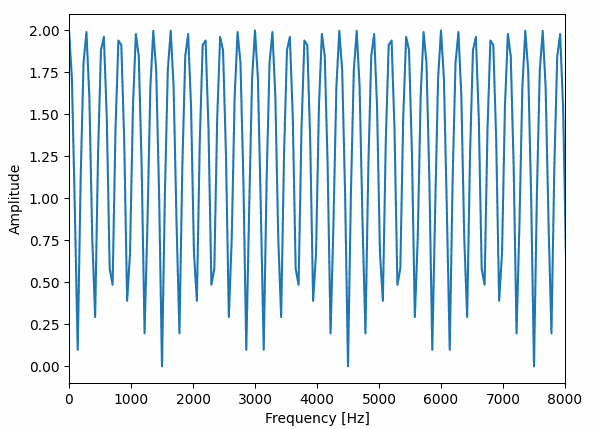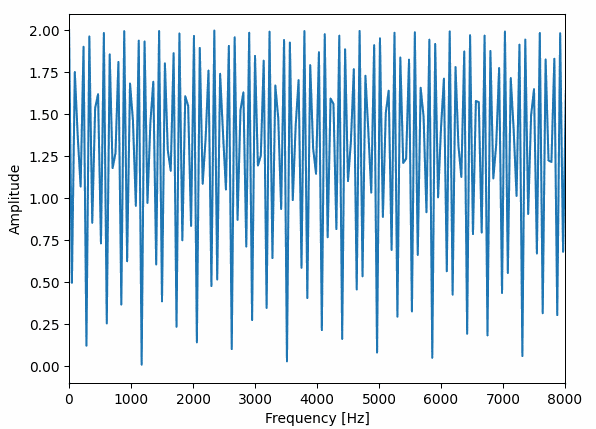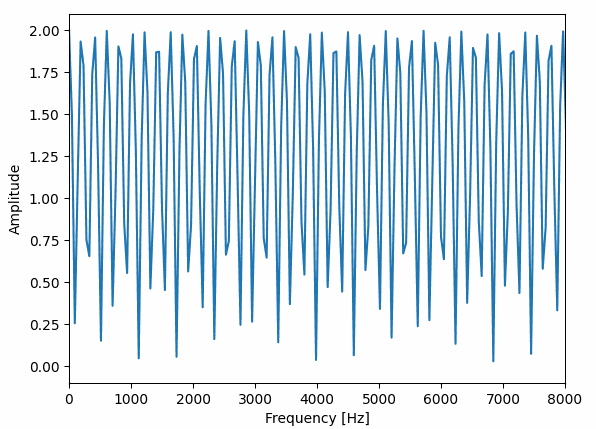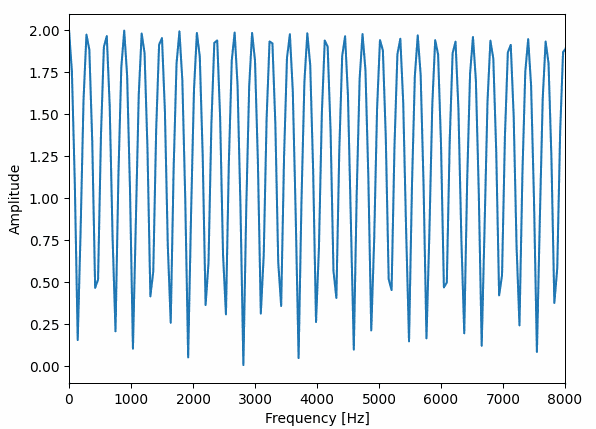
一方で d=0.002[s]、depth=0.002[s]、r=0.5[Hz]に設定したフランジャーの周波数特性は以下のようになります。
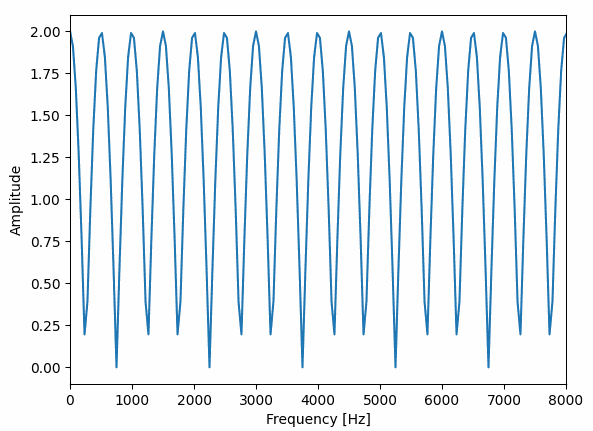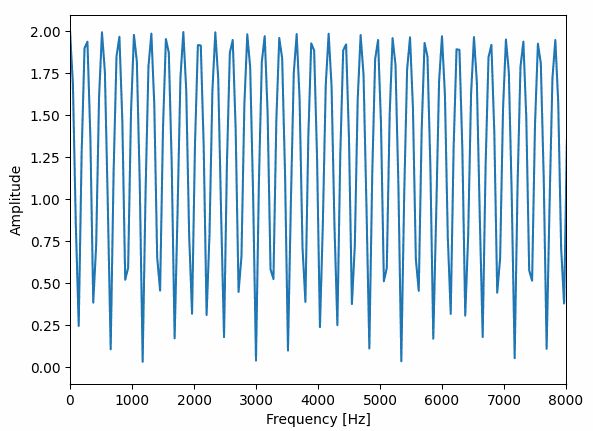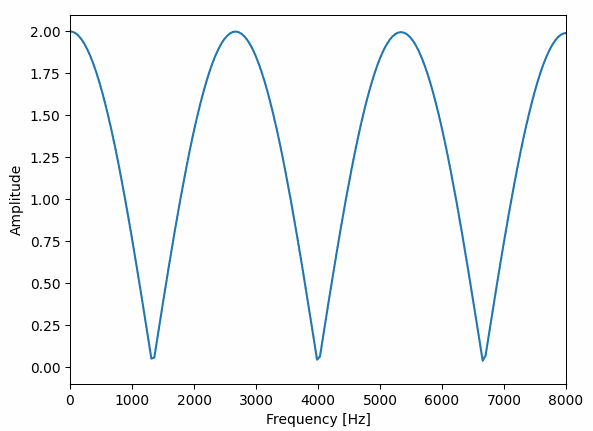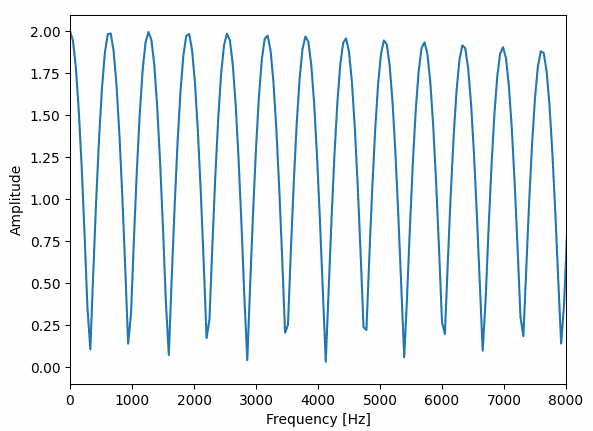
コーラスは短い時間でいろいろな形に変化していて、フランジャーはバネのように伸び縮みしている感じですね。
これだけ周波数特性に違いがあると別々のエフェクターの名前がつく理由もわかる気がします。
プログラム
コーラス・フランジャをかけるプログラムをPythonで実装しました。ソースコードと実行方法について説明します。
ソースコード
コーラス・フランジャーのソースコード chorus_flanger.py は以下です。
import soundfile as sf
import numpy as np
import math
# パラメータ
d = 0.025 # 平均遅延時間 [s]
r = 0.1 # RATE [Hz]
depth = 0.01 # DEPTH [s]
wav_in_name = "input.wav" # 入力WAVデータ名
wav_out_name = "output.wav" # 出力WAVデータ名
# WAVファイルを読み込む
x, fs = sf.read(wav_in_name)
# 必要な値を設定
length_x = x.shape[0] # 入力信号の長さ
y = np.zeros(length_x) # 出力信号
d = d * fs # [s]->[sample]
depth = depth * fs # [s]->[sample]
# 繰り返し処理
for n in range(length_x):
# 遅延時間
tau = d + depth * math.sin(2*math.pi*r*n/fs)
t = n - tau
# 線形補間
m = int(t)
if m+1 >= length_x: # 入力信号がなければ
break # 繰り返し処理を終了.
delta = t - m
y[n] = x[n]
y[n] += delta * x[m+1] + (1.0 - delta) * x[m]
if np.max(np.abs(y)) > 1.0:
y = y/np.max(np.abs(y)) # ノーマライズ
sf.write(wav_out_name, y, fs, subtype='PCM_16')24行目:ビブラートの遅延時間 τ を設定する。
27~33行目:ビブラートの遅延時間は整数とは限らず、サンプルとサンプルの中間値を求める必要がある。ここでは、以下のように線形補間によってその中間値を求める。
$$
\begin{align}
y[n] &= x[n] + \delta \cdot x[m] + (1-\delta) \cdot x[m+1] \\[4pt]
t &= n-\tau \\[4pt]
\delta &= t-m
\end{align}
$$
\(m\ \) は\(\ m\leq t < m+1\ \)という関係を満足する整数です。
36~37行目:オーバーフローしたとき、ノーマライズする。
実行方法
(1) プログラムを実行するディレクトリにソースコード(chorus_flanger.py)と入力 WAV データを格納する。
(2) ソースコード5~10行目のパラメータと入出力データ名を修正する。
# パラメータ
d = 0.025 # 平均遅延時間 [s]
r = 0.1 # RATE [Hz]
depth = 0.01 # DEPTH [s]
wav_in_name = "input.wav" # 入力WAVデータ名
wav_out_name = "output.wav" # 出力WAVデータ名
(3) 以下のコマンドで python を実行することで、コーラス・フランジャーのエフェクトをかけたWAVデータが出力される。
$ python chorus_flanger.py処理結果
以下のようにパラメータを設定して、ギターの音にエフェクトをかけました。
| パラメータ名 | 変数名 | 設定値 |
|---|---|---|
| 平均遅延時間 | d | 0.025 [s] |
| ビブラートの周波数 | r | 0.1 [Hz] |
| ビブラートの深さ | depth | 0.010 [s] |
| パラメータ名 | 変数名 | 設定値 |
|---|---|---|
| 平均遅延時間 | d | 0.002 [s] |
| ビブラートの周波数 | r | 0.5 [Hz] |
| ビブラートの深さ | depth | 0.002 [s] |
エフェクトをかけたギター音は以下のようになります。イヤホンやヘッドホンで聴かないと違いがわかりにくいです。
入力データ
コーラス後のデータ
フランジャー後のデータ
コーラスについては音の厚みが上がったように感じましたが、気のせいな感じもします。ちょっと入力のギター音が悪いですね。
フランジャーはたしかにジェット機のような音が聞こえたため、ジェットサウンドと呼ばれている理由がわかる気がします。
スペクトログラムを以下に示します。
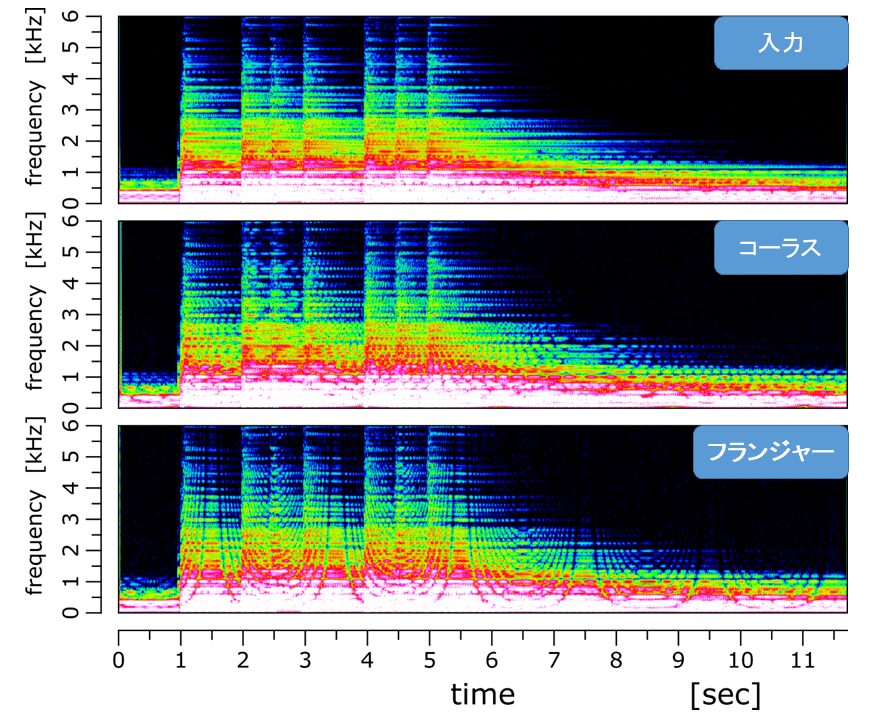
コーラスは各周波数成分が強調と抑制を繰り返しているのがわかります。
フランジャーは抑制されている箇所が模様のようになっており、規則的に抑制されている感じです。これがジェットサウンドの要因なのですかね?わからないけども...。
おわりに
本記事では、コーラスとフランジャーを実装してみました。いろいろ調べるとコーラスとフランジャーが同じ原理にもかかわらず、違う名前のエフェクターとなっている理由がわかる気がします。
入力に使用したギターについては自分で弾いたものを使用しました。出力結果との違いがわかるようにもう少しギターの練習はしておこうと思います。
■参考文献
[1] 青木直史、”C言語ではじめる音のプログラミング”、オーム社、2008.
[2] 川村新、”プログラム101付き音声信号処理”、CQ社、2021.
