頭部伝達関数(HRTF: Head-Related Transfer Function)を使って8D立体音響を Python で実装してみました。8D立体音響というのは正直言って私も厳密な定義はわかりませんが、この記事で言っているのはYoutubeによくある頭の周りをクルクルまわる音源のことです。
「左右のチャネルの音量を変えれば作れるのでは?」という声を聞きますが、それではできず、頭部伝達関数というものを使う必要があります。
注意点として、8D立体音響を作るソフトがどのように処理しているかはわからないため、細かいところは異なることをご承知おきください。
頭部伝達関数(HRTF)
頭部伝達関数とはヒトが音の方向を知覚するために重要な役割を果たすものです。
参考文献 [1] では、頭部伝達関数を以下のように定義しています。
音波は鼓膜に届く直前に頭や耳介,あるいは胴体の影響を受ける。このような,頭部周辺による入射音波の物理特性の変化を周波数領域で表現したものを頭部伝達関数という。
つまり、頭や耳、鼻などが与える音への影響のことです。
例えば、図のように左側に音源があるとき、音源と左耳の間には何もないため、音はあまり変化なく左耳に伝わります。一方、音源と右耳の間には頭や鼻という障害物があるため、右耳に伝わる音は減衰したり、左耳と比べると遅れて音が届いたりします。
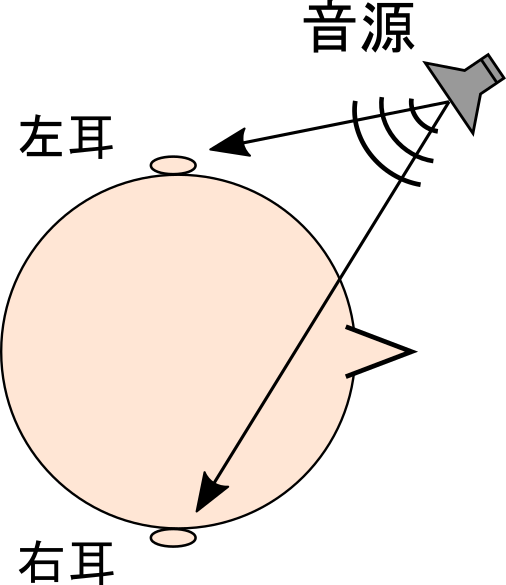
このように左右の耳で異なる音の伝わり方をすることで、ヒトは音の位置や方向を知覚できるそうです。冷静に考えると驚くハナシで、信号処理では音が到来する2次元方向を把握するのも結構難しいので、音源の3次元の方向や位置がわかる人間はすごいなと思います。
8D立体音響を作成する場合は、測定した頭部伝達関数を音データに作用させることで左右前後に音源があると錯覚させることができます。
頭の形などは個人差があるので、他人の頭部伝達関数を使うと前後方向については上手く錯覚させることはできませんが、左右方向については上手く錯覚させることができます。
頭の周りをまわる音源の作成
Youtube によくある頭の周りをまわる音源を作成したいと思います。
音源の位置の計算
音源が頭の周りをまわっている様子を図に示します。
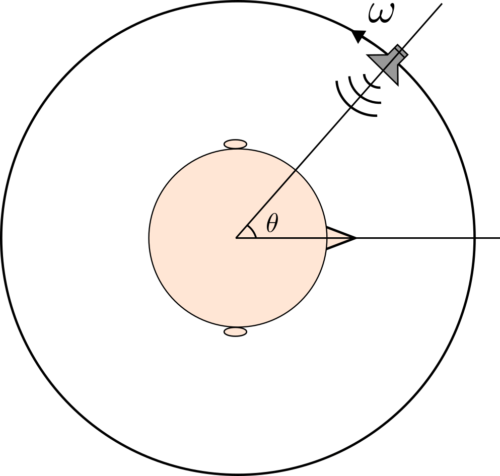
音源が図のように角速度\(\ \omega\) [deg/s] でまわっているとき、サンプル番号 n のときの音源方向角度\(\ \theta \) [deg] は以下のように求まります。
$$
\theta = \omega \frac{n}{f_s}
$$
ここで、\( f_s\) はサンプリング周波数です。
音源方向角度が360度以上の場合、プログラム上扱いにくいので、0度以上360度未満になるように360度の倍数で引きます。
頭部伝達関数の補間
今回使用するHRTFのデータベースは5度間隔でHRTFが測定されています。そのため、音源方向角度が7度や8度のような中途半端な場合、どのようなHRTFを使えばいいかという問題があります。
今回は、参考文献 [2] に記述されている線形2点補間を用いて、HRTFの補間を行います。計算は簡単で以下のようにHRTFを補間します。
$$
H[k] = rH_1[k] + (1-r)H_2[k]
$$
ここで、\(r\) は\(\ 0\leq r \leq 1\ \) の2つのHRTFの内分比を表します。例えば、音源方向角度が8度の場合、\( H_1 \)は5度のHRTF、\( H_2 \) は10度のHRTFを用いて、\( r \) は0.4とします。
補足:今回行う線形2点補間は参考文献 [2] のやり方とは少し異なっています。
参考文献 [2] ではHRTFの振幅応答を補間して求めて、位相応答はHRTFが最小位相フィルタとなるように求めています。
私の補間の仕方では位相が打ち消しあって、変な音になる可能性がありますが、処理した音はそこまで問題がなかったのでこのままにしています。
オーバーラップ加算法
いままでデータベースの中にはHRTFが入っているような言い方をしていましたが、厳密には頭部インパルス応答(HRIR:Head-Related Impulse Response)が入っています。HRIRをFFTすることでHRTFになります。
HRIRを波形データに畳み込めば、クルクルまわる音源ができますが、処理に時間がかかってしまいます。Pythonではfor文の処理が遅いため、なおさら計算時間がかかります。
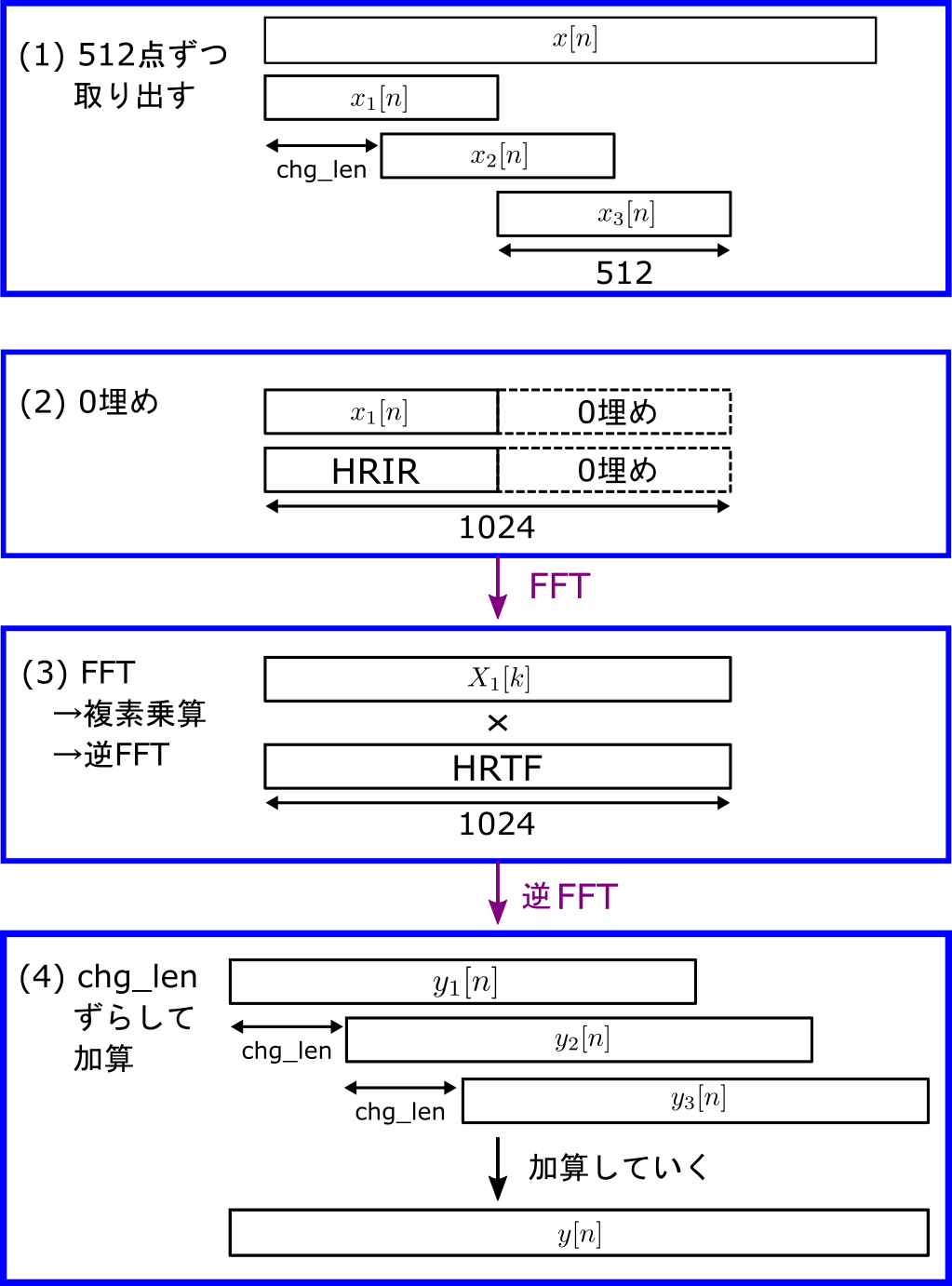
そこで、文献 [1] に記述されているオーバーラップ加算法 を行います。オーバーラップ加算法の手順は以下です。
- 音源信号 x からchg_len ずつずらしながらHRIRの長さ512点を取り出していく。
- 取り出した音源信号とHRIRに512点の0埋めを行う。
- FFT、複素乗算、逆FFTを施してデータ長 1024点の結果を得る。
- 処理した結果を加算していって、出力信号 y とする。
プログラム
8D立体音響を作成するプログラムは以下です。
更新(2024/04/20):SOFA形式の頭部伝達関数を使用する Python コードに変更しました。
import soundfile as sf
import numpy as np
from scipy.fft import rfft, irfft
import scipy.signal as sg
import pysofaconventions
from resampy import resample
# パラメータ
wav_name = "input.wav" # 読み込むWAVデータの名前
out_name = "output.wav" # 出力するWAVデータの名前
sofa_name = 'Subject1_HRIRs.sofa' # SOFAの名前
elev = 0 # 仰角
N = 2048 # HRTFの点数
chg_len = 128 # HRTFを変える間隔
omega = 90 # 角速度 [deg/s]
# WAVファイルを読み込む
x, fs = sf.read(wav_name)
x_len = len(x)
# 方位角0°~355°のHRIRを読み込む
## SOFAFileオブジェクトを読み込む
sofa = pysofaconventions.SOFAFile(sofa_name, 'r')
## サンプリング周波数を確認
sofa_fs = sofa.getVariableValue('Data.SamplingRate')
## WAVファイルをリサンプリング
x = resample(x, fs, sofa_fs[0])
## HRIR を抽出
hrir_all = sofa.getDataIR().data
## 仰角0度,距離0.76mのIRデータを抜き出す
sourcePositions = sofa.getVariableValue('SourcePosition')
hrir_l = np.zeros((72, N))
hrir_r = np.zeros((72, N))
for i, angle in enumerate(range(0,360,5)):
index = np.where(np.logical_and(sourcePositions[:,0]==angle, sourcePositions[:,1] == elev, sourcePositions[:,2] == 0.76))[0]
hrir = np.squeeze(hrir_all[index])
hrir_l[i,:] = hrir[0]
hrir_r[i,:] = hrir[1]
# FFT をして HRTF 作成
HRTF_L = np.zeros((72, N+1), dtype=np.complex128)
HRTF_R = np.zeros((72, N+1), dtype=np.complex128)
for m in range(72):
h = np.pad(hrir_l[m,:], [0,N], 'constant') # 0埋め
HRTF_L[m,:] = rfft(h)
h = np.pad(hrir_r[m,:], [0,N], 'constant') # 0埋め
HRTF_R[m,:] = rfft(h)
# 変数を初期化
n_frame = len(x) // chg_len + 1 # フレーム数
x = np.pad(x, [0,2*N])
y = np.zeros((len(x), 2))
# フレームごとに異なるHRTFを掛ける
for i in range(n_frame):
# 移動音源がどの角度にあるか計算
theta = omega * i * chg_len / fs
while int(theta) > 359: # 0<theta<360にする
theta = theta - 360
# HRTFを線形2点補間するためのパラメータを求める
m = theta / 5
m1 = int(m)
m2 = m1 + 1
if m2 == 72:
m2 = 0
r2 = m - int(m)
r1 = 1.0 - r2
# 取り出した x を FFT する
x_N = np.pad(x[i*chg_len:i*chg_len+N], [0,N], 'constant') # 0埋め
X = rfft(x_N)
# 補間したHRTF と X を掛ける
YL = X * (r1*HRTF_L[m1,:]+r2*HRTF_L[m2,:])
YR = X * (r1*HRTF_R[m1,:]+r2*HRTF_R[m2,:])
# 逆FFT をして足し合わせる
y[i*chg_len:i*chg_len+2*N, 0] += irfft(YL)
y[i*chg_len:i*chg_len+2*N, 1] += irfft(YR)
# ファイルに書き込む
if np.max(np.abs(y)) > 1:
y = y/np.max(y) # ノーマライズ
y = resample(y, sofa_fs[0], fs, axis=0)
sf.write(out_name, y[:x_len,:], fs, subtype="PCM_16")
21~42行目:pysofaconventionsを使って0度から355度のHRIRをnumpy配列に読みこんでいます。SOFAの読み込みは以下の方のブログを参考にしています。
需要が高まってきているバイノーラル処理にチャレンジする場合、まずはWeb上のSOFA形式のHRTFデータで試すことが多い…
44~51行目:読み込んだHRIRを0埋めして、FFTすることでHRTFを作成しています。
61~64行目:フレームごとに移動音源の角度を求めています。
66~73行目:HRTFを線形2点補間するためのパラメータを求めています。例えば、音源方向角度が17度の場合、17/5=3.4 でm1=3, m2=4 となります。インデックス3と4に対応するHRIRは15度と20度です。また、r2=3.4-3=0.4 、r1=1-r2=0.6 となり、線形補間のパラメータが求まります。
75~77行目:x から512点取り出して、0埋めをして、FFTをしています。
79~85行目:補間して求めたHRTFとXを乗算して、逆FFTをして、加算しています。
処理結果
頭部伝達関数を使って作成した8D立体音響は以下のようになります。仰角は0度、chg_lenは128点で作成しました。ヘッドホンやイヤホンでお聴きください。
入力音源
処理結果(角速度ω:30 [deg/s])
処理結果(角速度ω:120 [deg/s])
左右と後ろについては上手く定位されていますが、前方についてはあまり定位されていないように感じると思います。
音源が角速度ω:120 [deg/s] はさすがに少し気持ち悪くなりますね。
おわりに
HRTFを使って8D立体音響を実装してみました。Youtubeの8D立体音響ではボーカルだけこのような処理をして、他の伴奏とかは普通にミックスしているのかもしれません。あとはコンサートホールなどのインパルス応答も畳み込んだりして、いい感じにしているのだろうと思います。
■参考文献
[1] 飯田 一博、”頭部伝達関数の基礎と3次元音響システムへの応用”、コロナ社、2017.
[2] 西野隆典, 梶田将司, 武田一哉, 板倉文忠, "水平方向及び仰角方向に関する頭部伝達関数の補間," 日本音響学会誌, 57巻, 11号, pp.685-692, 2001.
■使用したデータについて
この記事で信号処理した楽曲は Pixabay で提供されているものを使用させていただきました。
【楽曲情報】
"Whistle Joyride" 2024 Top-Flow (Public Domain)
頭部伝達関数につきましてはThe 3D3A Lab at Princeton University のデータベースから使用させていただきました。
【頭部伝達関数データベース情報】
[1]. R. Sridhar and E. Choueiri. The 3D3A Lab Head-Related Transfer Function Database. 3D3A Lab Technical Report #3, October 2021 (upcoming).
[2]. R. Sridhar, J. G. Tylka, and E. Y. Choueiri. A database of head-related transfer function and morphological measurements. In Audio Engineering Society Convention 143, October 2017.