
Python で片側 t 検定を行うプログラムを実装いたしました。
音声・音響信号処理の研究では提案手法が従来手法よりも優れていることを示すために聴取実験による主観評価を行うことが多いです。
その際、提案手法の評価値の平均が従来手法よりも上回っているかだけでなく、有意差があるかどうか調べる必要があります。有意差があることを確認するために片側 t 検定を行いました。
片側 t 検定
今回、従来手法と提案手法を5段階評価してもらい、以下のデータに対して「提案手法が従来手法よりも評価が高い」かどうかを t 検定で調べました。
| 番号 | 従来手法 | 提案手法 |
|---|---|---|
| 1 | 1 | 3 |
| 2 | 2 | 3 |
| 3 | 2 | 4 |
| 4 | 2 | 2 |
| 5 | 3 | 2 |
| 6 | 4 | 4 |
| 7 | 2 | 3 |
| 8 | 3 | 3 |
| 9 | 4 | 4 |
| 10 | 4 | 3 |
| 11 | 3 | 3 |
| 12 | 5 | 5 |
| 13 | 2 | 2 |
| 14 | 3 | 3 |
| 15 | 3 | 4 |
| 16 | 3 | 2 |
| 17 | 4 | 4 |
| 18 | 4 | 4 |
仮説を立てる
サンプルサイズ n、従来手法の評価値を\(x_{i} (i=1,\cdots,n)\)、提案手法の評価値を \(y_{i}\)、評価値の差を \(d_{i} = y_{i} - x_{i} \)、評価値の差の母平均を \(\mu\) として、仮説は以下のように立てました。
・帰無仮説 \(H_0\): \(\mu = 0\)
・対立仮説 \(H_1\): \(\mu > 0\)
片側 t 検定を用いて帰無仮説を棄却することで「評価値の差の母平均は0より大きい」を採択し、「提案手法が従来手法よりも評価が高い」と主張できるようにします。
有意水準αを設定する
有意水準とは帰無仮説が真にもかかわらずに、それを棄却する可能性のことです。一般には、有意水準αは 5% か 1% を設定するそうです。
今回は α=5% としました。
棄却限界値 c を決定する
評価値の差の分布 D が正規分布に従うとき、
$$
T = \frac{\overline{X}_{D}-\mu}{S/\sqrt{n}}
$$
は自由度 n-1 の t 分布に従います。ここで、\( \overline{X}_D\) は評価値の差の標本平均の分布、S は評価値の差の標本標準偏差の分布を表します。
今回、サンプルサイズは n=18 のため、T は自由度 n-1=17 の下図の t 分布に従います。累積分布関数 F(X) も載せておきます。
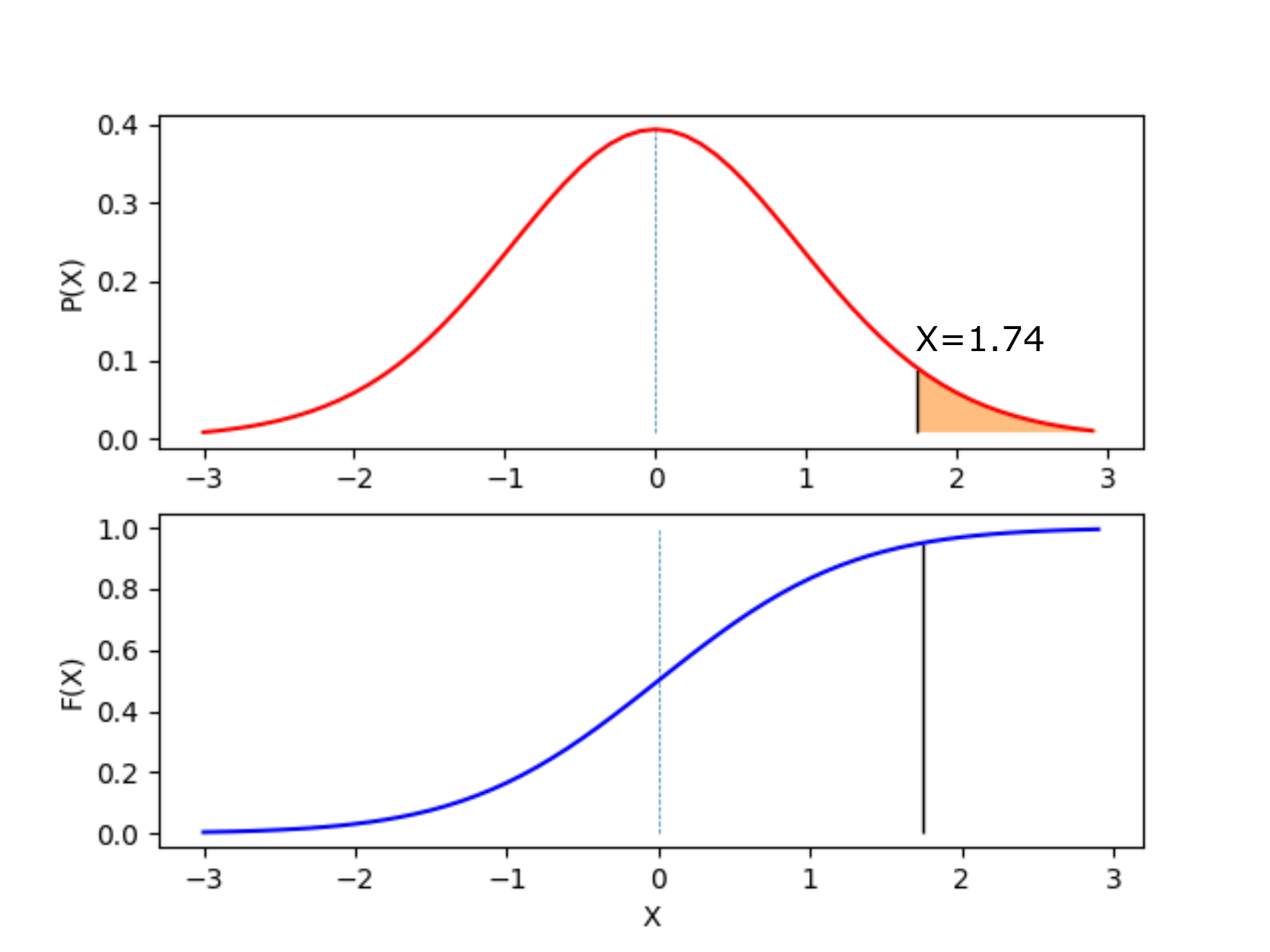
自由度 n-1=17 の t 分布の分布関数 F(X) が \(1-\alpha=0.95\) となるときは \(X=1.74\) であるため、棄却限界値は \(c=1.74\) となります。
それなので、帰無仮説を棄却するためには、今回の評価値で計算された t の値が t>c でなければなりません。
検定統計量 t を求める
今回、\(\mu=0\ \)と帰無仮説を立て、\(\overline{X}_{D}\) と \(S\) の観測値は \(\overline{d}=0.222\)、\(s=0.878\) であったため、
$$
t = \frac{0.222-0}{0.878/\sqrt{18}} \fallingdotseq 1.073
$$
で、c>t となってしまいました。このため、帰無仮説は棄却できず、提案手法と従来手法の間に有意差を確認できませんでした。
プログラム
Pythonで t 検定を行うプログラムを実装しました。
ソースコード
2つのデータに対して t 検定で有意差を確認するソースコード (t_test.py) は以下です。
import numpy as np
from scipy.stats import t
path = "eval_value.txt" # データファイル
alpha = 0.05 # 有意水準
x = [] # 従来手法の評価値の配列
y = [] # 提案手法の評価値の配列
# ファイルから評価値取得
with open(path) as f:
for s_line in f:
x_temp, y_temp = s_line.split()
x.append(float(x_temp))
y.append(float(y_temp))
x = np.array(x)
y = np.array(y)
d = y-x
n = d.size # サンプルサイズ
# 棄却限界値を求める
c = t(n-1).ppf(1.0-alpha)
# 評価値の差の平均を求める
mu = np.mean(d)
# 評価値の差の標準偏差を求める
s = np.sqrt(np.sum((d - mu)**2)/(n-1))
# t値を求める
t = mu*np.sqrt(n)/s
if t > c:
print("提案手法と従来手法に有意差を確認しました。")
else:
print("提案手法と従来手法に有意な差は確認できませんでした")
# 各値の表示
print("size=%d, mean=%f, sd=%f" % (n, mu, s))
print("c=%f, t=%f" % (c, t))実行方法
(1) プログラムを実行するディレクトリにソースコード(t_test.py)を格納する。また、以下のように1列目に従来手法の評価値、2列目に提案手法の評価値が並んでいるファイルを格納する。
1 3
2 3
2 4
2 2
3 2
4 4
2 3
3 3
4 4
4 3
3 3
5 5
2 2
3 3
3 4
3 2
4 4
4 4(2) ソースコード4, 5行目のt検定するデータファイル名と有意水準を修正する。
path = "eval_value.txt" # データファイル
alpha = 0.05 # 有意水準
(3) 以下のコマンドで python を実行することで、t検定の結果が出力される。
$ python t_test.py
提案手法と従来手法に有意な差は確認できませんでした
size=18, mean=0.222222, sd=0.878204
c=1.739607, t=1.073565おわりに
本記事では、Python で 片側 t 検定を行うプログラムを実装致しました。結果は残念でしたが、有意差がないことを確認できてよかったです。
■参考文献
[1] E.クライツィグ著、田栗正章訳「確率と統計 (技術者のための高等数学)」、培風館、2004年
[2] 24-2. 母平均の検定(片側t検定) | 統計学の時間 | 統計WEB、閲覧日: 2024年1月20日
