Pythonで正弦波モデルを実装

Pythonを使って正弦波モデルを実装しました。ソースコードがネット上にあまりないため、頑張って自力で書きました。 今回は、M&Qアルゴリズムとよばれる方法で実装を行っています。

目次

正弦波モデルとは

正弦波モデルとは正弦波に似ている信号を足し合わせて音声や楽音などを表現する方法です。

音声のスペクトログラムの例を以下に示します。

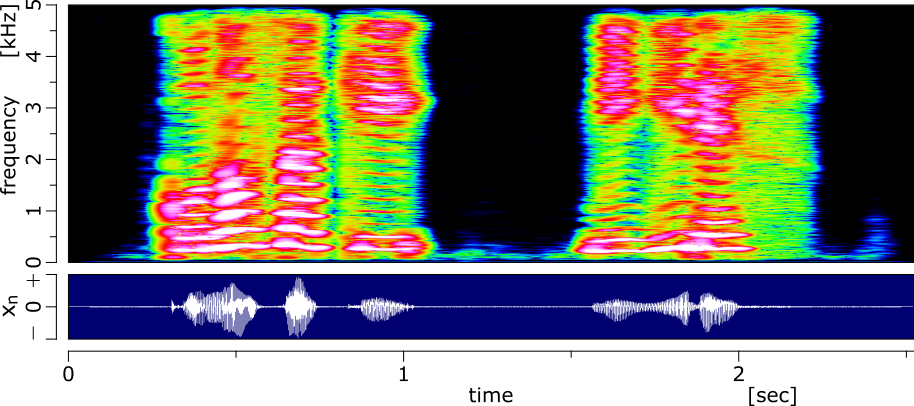
図：音声のスペクトログラム
図：音声のスペクトログラムの例

音声のスペクトログラムでは、周波数方向に間隔をあけてエネルギーが多い箇所があり、こういう特徴を調波構造と呼んだりします。正弦波モデルでは、こういうエネルギーが多い箇所を振幅と周波数が滑らかに時間変化する正弦波で近似します。

正弦波モデルの用途としては、元信号よりも少ないデータで信号を近似するので、音声圧縮で使われたりします（MP3とかはこの方法を使いませんが...）。また、正弦波モデルによって調波成分ごとに操作が可能となるため、信号処理の前段階としても使われている印象です。

プログラム

記述したプログラムについて説明します。正直いって、論文の内容で見逃している点やバグがあるかもしれないので、参考程度にしていただければ幸いです。

プログラムは一つのファイル main.py に記述しています。また、モノラル音源のみに対応しており、ステレオには対応していません。

main.py（クリックで展開） 
import soundfile as sf
import numpy as np
import scipy.signal as sg
import cmath
import datetime
from librosa import resample, stft, display
import matplotlib.pyplot as plt

PEAK        = 1
CONNECT     = 2
DEATH       = 3
BIRTH       = 4
DEATH_BIRTH = 5

# フレームごとの極大値を検知
def DetectPeak(X):

    # 全てゼロのnumpy配列の作成
    peak_plane = np.zeros(X.shape, dtype=int)
    # 極大値の箇所を検知
    index = sg.argrelextrema(X, np.greater, axis=0, order=1)
    # 極大値の箇所に１を代入
    peak_plane[index] = PEAK

    return peak_plane

# フレーム間ピークマッチング
def PeakMatching(peak_plane):

    n_bin = peak_plane.shape[0]    # ビン数
    n_frame = peak_plane.shape[1]  # フレーム数
    link_flag = False              # 接続先があるかのフラグ 
    candidate_match = n_bin        # 接続先の候補1
    next_candidate_match = n_bin   # 接続先の候補2

    # 全てゼロのnumpy配列の作成
    track_plane = np.ones(peak_plane.shape, dtype=int) * (-1)

    for i in range(n_frame-1):
        for k in range(n_bin):

            # 極大値の箇所を検知
            if peak_plane[k,i]==PEAK or peak_plane[k,i]==CONNECT:

                # 前の極大値で接続先があったとき
                if link_flag == True:
                    # step2(c)
                    if abs(pre_peak-candidate_match) < abs(k-candidate_match):
                        track_plane[pre_peak,i] = candidate_match
                        peak_plane[candidate_match, i+1] = CONNECT
                    else:
                        # step2(d)
                        if next_candidate_match > candidate_match:
                            track_plane[pre_peak,i] = pre_peak     
                            peak_plane[pre_peak,i+1] = DEATH
                        # step2(e)
                        else:
                            track_plane[pre_peak,i] = next_candidate_match
                            peak_plane[next_candidate_match, i+1] = CONNECT

                # 初期化
                link_flag = False
                candidate_match = n_bin
                next_candidate_match = n_bin

                # 接続先候補を探す
                if k < delta_bin:
                    for j in range(-k,delta_bin+1):
                        if peak_plane[k+j,i+1]==PEAK:
                            link_flag = True
                            if abs(j) < abs(candidate_match):
                                next_candidate_match = candidate_match 
                                candidate_match = k+j  #step1(b)
                elif k >= n_bin-delta_bin: 
                    for j in range(-delta_bin,n_bin-k):
                        if peak_plane[k+j,i+1]==PEAK:
                            link_flag = True
                            if abs(j) < abs(candidate_match):
                                next_candidate_match = candidate_match 
                                candidate_match = k+j  #step1(b)
                else:
                    for j in range(-delta_bin,delta_bin+1):
                        if peak_plane[k+j,i+1]==PEAK:
                            link_flag = True  
                            if abs(j) < abs(candidate_match):
                                next_candidate_match = candidate_match 
                                candidate_match = k+j  #step1(b)

                # 接続先がなかった場合
                if link_flag==False:
                    track_plane[k,i]  = k 
                    peak_plane[k,i+1] = DEATH

                # 極大値の位置の保存
                pre_peak = k

            #　trackがDEATHのとき
            elif peak_plane[k,i]==DEATH:
                track_plane[k,i] = (-2)  # step1(a) DEATHとする

        # 前の極大値で接続先があったとき
        if link_flag == True:
            track_plane[pre_peak,i] = candidate_match
            peak_plane[candidate_match, i+1] = CONNECT

        # i+1フレームに接続されてない極大値がないか確認
        for k in range(n_bin):
            # step3(f) BIRTHとする
            if peak_plane[k,i+1]==PEAK:
                track_plane[k,i] = k
                peak_plane[k,i+1] = CONNECT      
                if peak_plane[k,i]==DEATH:
                    peak_plane[k,i] = DEATH_BIRTH
                else:
                    peak_plane[k,i] = BIRTH

    return track_plane

# 音声合成（位相補間と振幅補間）
def SynthesizeSpeech(X, peak_plane, track_plane):

    n_bin = X.shape[0]                # ビン数
    n_frame = X.shape[1]              # フレーム数
    y = np.zeros(x_shape)             # 出力信号
    n = np.arange(hop_length)         # サンプル番号
    t = np.arange(hop_length)/sr_o    # 時間
    r_arr = np.zeros(hop_length)      # 振幅の一時保存
    theta_arr = np.zeros(hop_length)  # 位相の一時保存

    for i in range(n_frame-1):
        for k in range(n_bin):

            # 極大値、DEATH、BIRTHを判定
            if peak_plane[k,i] == CONNECT or 
               peak_plane[k,i] == BIRTH or 
               peak_plane[k,i] == DEATH_BIRTH:

                # 振幅と位相と角周波数
                if peak_plane[k,i] == BIRTH or peak_plane[k,i] == DEATH_BIRTH:
                    r1 = 0
                else:
                    if k==0 or k==n_bin-1:
                        r1 = abs(X[k,i])
                    else:
                        r1 = 2.0 * abs(X[k,i])
                theta1 = cmath.phase(X[k,i])
                omega1 = k * omega_b
                if peak_plane[k,i+1] == DEATH or peak_plane[k,i+1] == DEATH_BIRTH:
                    r2 = 0
                else:
                    if track_plane[k,i]==0 or track_plane[k,i]==n_bin-1:
                        r2 = abs(X[track_plane[k,i],i+1])
                    else:
                        r2 = 2.0 * abs(X[track_plane[k,i],i+1])
                theta2 = cmath.phase(X[track_plane[k,i],i+1])
                omega2 = track_plane[k,i] * omega_b

                # Mの計算
                M = ((theta1+omega1*T-theta2)+(omega2-omega1)*T/2.0)/(2.0*np.pi)
                M = round(M)

                # alphaとbeta
                matrixup = theta2-theta1-omega1*T+M*2.0*np.pi
                matrixdw = omega2-omega1
                alpha = matrixup*(3.0/(T**2))-matrixdw/T
                beta  = matrixup*(-2.0/(T**3))+matrixdw/(T**2)

                # r, theta計算とyに足し合わせる
                r_arr = r1+(r2-r1)*n/(hop_length)
                theta_arr = theta1+omega1*t+alpha*(t**2)+beta*(t**3)
                y[i*hop_length:(i+1)*hop_length] += r_arr*np.cos(theta_arr)

    return y

# パラメータ
path = "Vox.wav"
sr_o = 10000
n_fft = 512
hop_length = 256
delta_freq = 50
window = sg.windows.get_window('hamming', n_fft)
window = window / np.sum(window)

# WAVファイル読み込みとリサンプリング
x, sr = sf.read(path)
x = resample(x, sr, sr_o)
sf.write("sample.wav", x, sr_o, subtype='PCM_16')

# 必要な計算をあらかじめ行う
delta_bin  = int(delta_freq / (sr_o/n_fft))
T = hop_length/sr_o
omega_b = 2.0 * np.pi *(sr_o/n_fft)
x_shape = x.shape

# 計測スタート
start_time = datetime.datetime.now()

# 短時間フーリエ変換
X = stft(x, n_fft, hop_length, None, window)

# フレームごとの極大値を検知
peak_plane = DetectPeak(X)

# フレーム間ピークマッチング
track_plane = PeakMatching(peak_plane)

# 音声合成（位相補間と振幅補間）
y = SynthesizeSpeech(X, peak_plane, track_plane)

# 処理時間の出力
elapsed_time = datetime.datetime.now() - start_time
print("time: %s" % (elapsed_time))

# WAVファイル出力
sf.write("soundout.wav", y, sr_o, subtype='PCM_16')

メイン処理

メインの処理プログラム箇所は以下です。

import soundfile as sf
import numpy as np
import scipy.signal as sg
import cmath
import datetime
from librosa import resample, stft, display
import matplotlib.pyplot as plt

PEAK        = 1
CONNECT     = 2
DEATH       = 3
BIRTH       = 4
DEATH_BIRTH = 5

# フレームごとの極大値を検知
def DetectPeak(X):
~ 略 ~

# フレーム間ピークマッチング
def PeakMatching(peak_plane):
~ 略 ~

# 音声合成（位相補間と振幅補間）
def SynthesizeSpeech(X, peak_plane, track_plane):
~ 略 ~

# パラメータ
path = "Vox.wav"
sr_o = 10000
n_fft = 512
hop_length = 256
delta_freq = 50
window = sg.windows.get_window('hamming', n_fft)
window = window / np.sum(window)

# WAVファイル読み込みとリサンプリング
x, sr = sf.read(path)
x = resample(x, sr, sr_o)
sf.write("sample.wav", x, sr_o, subtype='PCM_16')

# 必要な計算をあらかじめ行う
delta_bin  = int(delta_freq / (sr_o/n_fft))
T = hop_length/sr_o
omega_b = 2.0 * np.pi *(sr_o/n_fft)
x_shape = x.shape

# 計測スタート
start_time = datetime.datetime.now()

# 短時間フーリエ変換
X = stft(x, n_fft, hop_length, None, window)

# フレームごとの極大値を検知
peak_plane = DetectPeak(X)

# フレーム間ピークマッチング
track_plane = PeakMatching(peak_plane)

# 音声合成（位相補間と振幅補間）
y = SynthesizeSpeech(X, peak_plane, track_plane)

# 処理時間の出力
elapsed_time = datetime.datetime.now() - start_time
print("time: %s" % (elapsed_time))

# WAVファイル出力
sf.write("soundout.wav", y, sr_o, subtype='PCM_16')

メインの処理では、以下の手順で音声を再合成しています。

  1. 音声を読み込む
  2. リサンプリングする
  3. 短時間フーリエ変換をする
  4. フレームごとに極大値（ピーク）を検知
  5. フレームどうしのピークをつなげる
  6. フレーム間の位相補間と振幅補間
  7. 音声を出力する

注意：窓関数\( w[n]\) については以下の式を満たすように補正しています。

$$
\sum_{n=-N/2}^{N/2} w[n] = 1
$$

ここで、\( N\) は窓関数の幅です。

なぜ、このようなことをするかというと、補正していない窓関数を使うと短時間フーリエ変換後の各要素のパワーと元信号のパワーを単純比較できなくなるからです。

補正に関しては以下の方のブログがわかりやすいです。

WATLAB -Python, 信号処理, 画像処理, AI, 工学, Web-
窓関数使用時の補正！FFTの時に忘れがちな計算とは？

FFTのプログラムを書いていて、窓関数の必要性に気付いて使ってみると振幅レベルが理論値と異なるということに気付くと思いま…

フレームごとに極大値の検知

フレームごとに極大値の検知をする DetectPeak の関数定義は以下になります。

# フレームごとの極大値を検知
def DetectPeak(X):

    # 全てゼロのnumpy配列の作成
    peak_plane = np.zeros(X.shape, dtype=int)
    # 極大値の箇所を検知
    index = sg.argrelextrema(X, np.greater, axis=0, order=1)
    # 極大値の箇所に１を代入
    peak_plane[index] = PEAK

    return peak_plane

極大値がある箇所に PEAK(1) を代入して、極大値ではない箇所は０とする2次元配列 peak_plane を作成します。

DetectPeak の出力は以下の図のようになります。

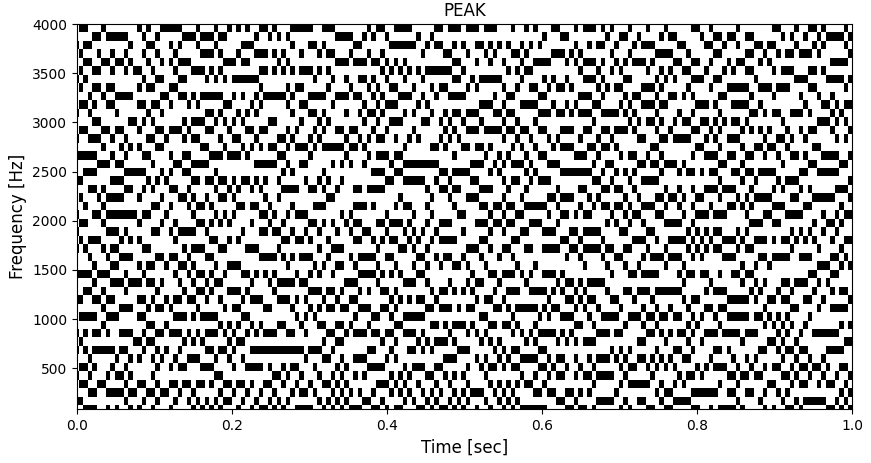
図：関数DetectPeakの出力
図：関数DetectPeakの出力

補足：Pythonでfor文を使うと、基本的に処理が遅いので、scipy.signal にある argrelextrema を使用して、極大値を検知しました。

フレーム間ピークマッチング

フレーム間ピークマッチングする PeakMatching の関数定義は以下になります。

# フレーム間ピークマッチング
def PeakMatching(peak_plane):

    n_bin = peak_plane.shape[0]    # ビン数
    n_frame = peak_plane.shape[1]  # フレーム数
    link_flag = False              # 接続先があるかのフラグ 
    candidate_match = n_bin        # 接続先の候補1
    next_candidate_match = n_bin   # 接続先の候補2

    # 全てゼロのnumpy配列の作成
    track_plane = np.ones(peak_plane.shape, dtype=int) * (-1)

    for i in range(n_frame-1):
        for k in range(n_bin):

            # 極大値の箇所を検知
            if peak_plane[k,i]==PEAK or peak_plane[k,i]==CONNECT:

                # 前の極大値で接続先があったとき
                if link_flag == True:
                    # step2(c)
                    if abs(pre_peak-candidate_match) < abs(k-candidate_match):
                        track_plane[pre_peak,i] = candidate_match
                        peak_plane[candidate_match, i+1] = CONNECT
                    else:
                        # step2(d)
                        if next_candidate_match > candidate_match:
                            track_plane[pre_peak,i] = pre_peak     
                            peak_plane[pre_peak,i+1] = DEATH
                        # step2(e)
                        else:
                            track_plane[pre_peak,i] = next_candidate_match
                            peak_plane[next_candidate_match, i+1] = CONNECT

                # 初期化
                link_flag = False
                candidate_match = n_bin
                next_candidate_match = n_bin

                # 接続先候補を探す
                if k < delta_bin:
                    for j in range(-k,delta_bin+1):
                        if peak_plane[k+j,i+1]==PEAK:
                            link_flag = True
                            if abs(j) < abs(candidate_match):
                                next_candidate_match = candidate_match 
                                candidate_match = k+j  #step1(b)
                elif k >= n_bin-delta_bin: 
                    for j in range(-delta_bin,n_bin-k):
                        if peak_plane[k+j,i+1]==PEAK:
                            link_flag = True
                            if abs(j) < abs(candidate_match):
                                next_candidate_match = candidate_match 
                                candidate_match = k+j  #step1(b)
                else:
                    for j in range(-delta_bin,delta_bin+1):
                        if peak_plane[k+j,i+1]==PEAK:
                            link_flag = True  
                            if abs(j) < abs(candidate_match):
                                next_candidate_match = candidate_match 
                                candidate_match = k+j  #step1(b)

                # 接続先がなかった場合
                if link_flag==False:
                    track_plane[k,i]  = k 
                    peak_plane[k,i+1] = DEATH

                # 極大値の位置の保存
                pre_peak = k

            #　trackがDEATHのとき
            elif peak_plane[k,i]==DEATH:
                track_plane[k,i] = (-2)  # step1(a) DEATHとする

        # 前の極大値で接続先があったとき
        if link_flag == True:
            track_plane[pre_peak,i] = candidate_match
            peak_plane[candidate_match, i+1] = CONNECT

        # i+1フレームに接続されてない極大値がないか確認
        for k in range(n_bin):
            # step3(f) BIRTHとする
            if peak_plane[k,i+1]==PEAK:
                track_plane[k,i] = k
                peak_plane[k,i+1] = CONNECT      
                if peak_plane[k,i]==DEATH:
                    peak_plane[k,i] = DEATH_BIRTH
                else:
                    peak_plane[k,i] = BIRTH

    return track_plane

PeakMatching は以下の図のようにピークの接続先のビン番号を記録した2次元配列 track_planeを出力します。ピークではない箇所は (-1) となっており、接続先がないときは (-2) とします。

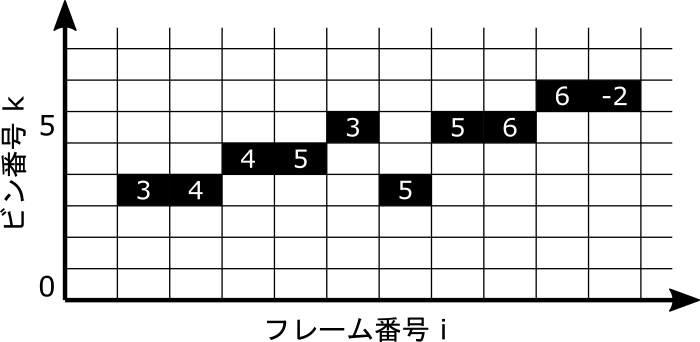
図：PeakMatching の出力の模式図
図：PeakMatching の出力の模式図

ピークの接続は以下の手順で決めます。

STEP1

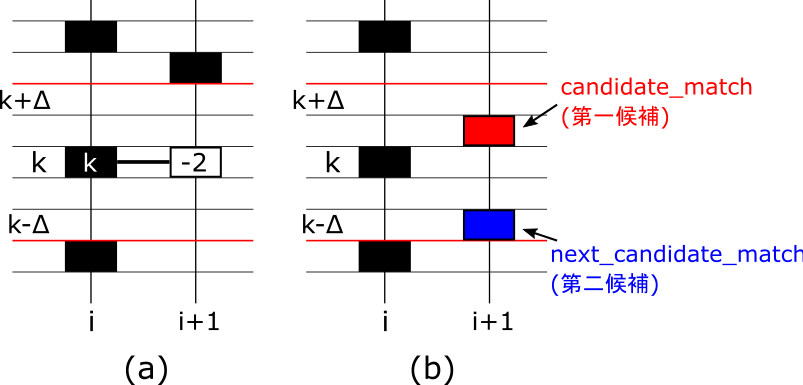
図：STEP1のピークマッチングの模式図
図：STEP1のピークマッチングの模式図

まず、パラメータとして Δ(delta_bin) を決めておきます。フレーム i、ビン番号 kにピークがある場合、次のフレームの [k-Δ, k+Δ] の範囲にピークがなければ、接続先はないものとします。接続先がないときは、図(a) のように track_plane[k,i]=k 、track_plane[k,i+1]=(-2) を代入します。

一方、 [k-Δ, k+Δ] の範囲にピークがあれば、接続先の第一候補のビン番号(candidate_match)と第二候補のビン番号(next_candidate_match)を保存しておいて、STEP2 に移行します。

ピークの接続先がなくなった箇所（track_plane[k,i+1]=(-2)を代入した箇所）については、peak_plane[k,i+1]=DEATH(3)を代入します。

STEP2

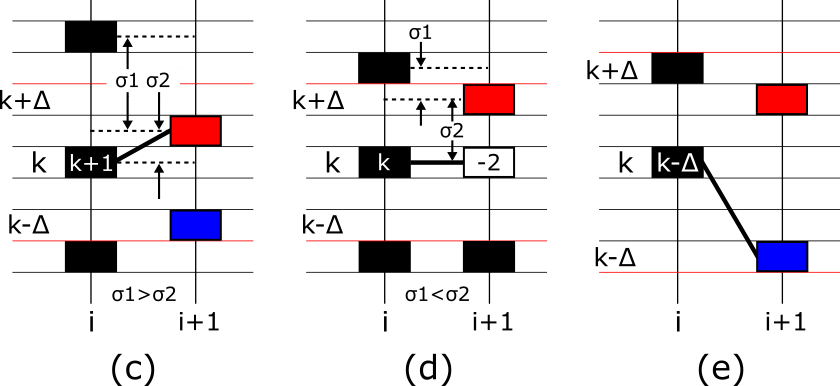
図：STEP2のピークマッチングの模式図
図：STEP2のピークマッチングの模式図

接続先候補のピークがある場合、次のピークと現在のピークのどちらが接続先第一候補（candidate_match）と近いか比較します。

現在のピークの方が近い場合（σ1>σ2）、図(c)のようにtrack_plane[k,i]=candidate_match を代入します。

次のピークの方が近くて（σ1<σ2）、candidate_match<next_candidate_matchの場合、図(d)のように track_plane[k,i]=k、track_plane[k,i+1]=(-2) を代入します。

次のピークの方が近くて（σ1<σ2）、candidate_match>next_candidate_matchの場合、図(e)のように track_plane[k,i]=next_candidate_match を代入します。

前のフレームのピークと接続されたピークの場所については、peak_plane[k,i]=CONNECT(2) を代入します。また、STEP1と同様にtrack_plane[k,i+1]=(-2)を代入した箇所については、
peak_plane[k,i+1]=DEATH(3)を代入します。

STEP3

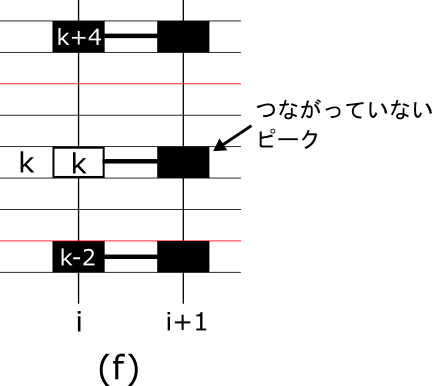
図：STEP3のピークマッチングの模式図
図：STEP3のピークマッチングの模式図

フレーム i の全ピークの接続先が決まったら、フレーム(i+1) で接続されていないピークがあれば、track_plane[k,i]=k、peak_plane[k,i]=BIRTH(4) を代入します（図(f)）。また、既にpeak_plane[k,i]=DEATH(2)となっていた場合、peak_plane[k,i]=DEATH_BIRTH(5)とします。

位相補間と振幅補間

位相補間と振幅補間をする SynthesizeSpeech の関数定義は以下になります。

# 音声合成（位相補間と振幅補間）
def SynthesizeSpeech(X, peak_plane, track_plane):

    n_bin = X.shape[0]                # ビン数
    n_frame = X.shape[1]              # フレーム数
    y = np.zeros(x_shape)             # 出力信号
    n = np.arange(hop_length)         # サンプル番号
    t = np.arange(hop_length)/sr_o    # 時間
    r_arr = np.zeros(hop_length)      # 振幅の一時保存
    theta_arr = np.zeros(hop_length)  # 位相の一時保存

    for i in range(n_frame-1):
        for k in range(n_bin):

            # 極大値、DEATH、BIRTHを判定
            if peak_plane[k,i] == CONNECT or 
               peak_plane[k,i] == BIRTH or 
               peak_plane[k,i] == DEATH_BIRTH:

                # 振幅と位相と角周波数
                if peak_plane[k,i] == BIRTH or peak_plane[k,i] == DEATH_BIRTH:
                    r1 = 0
                else:
                    if k==0 or k==n_bin-1:
                        r1 = abs(X[k,i])
                    else:
                        r1 = 2.0 * abs(X[k,i])
                theta1 = cmath.phase(X[k,i])
                omega1 = k * omega_b
                if peak_plane[k,i+1] == DEATH or peak_plane[k,i+1] == DEATH_BIRTH:
                    r2 = 0
                else:
                    if track_plane[k,i]==0 or track_plane[k,i]==n_bin-1:
                        r2 = abs(X[track_plane[k,i],i+1])
                    else:
                        r2 = 2.0 * abs(X[track_plane[k,i],i+1])
                theta2 = cmath.phase(X[track_plane[k,i],i+1])
                omega2 = track_plane[k,i] * omega_b

                # Mの計算
                M = ((theta1+omega1*T-theta2)+(omega2-omega1)*T/2.0)/(2.0*np.pi)
                M = round(M)

                # alphaとbeta
                matrixup = theta2-theta1-omega1*T+M*2.0*np.pi
                matrixdw = omega2-omega1
                alpha = matrixup*(3.0/(T**2))-matrixdw/T
                beta  = matrixup*(-2.0/(T**3))+matrixdw/(T**2)

                # r, theta計算とyに足し合わせる
                r_arr = r1+(r2-r1)*n/(hop_length)
                theta_arr = theta1+omega1*t+alpha*(t**2)+beta*(t**3)
                y[i*hop_length:(i+1)*hop_length] += r_arr*np.cos(theta_arr)

    return y

正弦波モデルのフレーム間の位相補間と振幅補間を行い、音声を再合成します。

フレーム i、ビン番号 k にピークがあるとき、接続先のビン番号を k' とすると、正弦波モデルのフレームごとの振幅と位相と周波数を以下のように計算します。

$$
\begin{align}
{\rm (i,k)} の振幅:\ & r_1 = 2 |X[k,i]| \\[5pt] {\rm (i+1,k')} の振幅:\ & r_2 = 2 |X[k',i]| \\[5pt] {\rm (i,k)} の位相:\ & \theta_1 = {\rm arg}(X[k,i])\\[5pt] {\rm (i+1,k')} の位相:\ & \theta_2 = {\rm arg}(X[k',i])\\[5pt] {\rm (i,k)} の周波数:\ & \omega_1 = 2 \pi k \frac{f_s}{N_F}\\[5pt] {\rm (i+1,k')} の周波数:\ & \omega_2 = 2 \pi k' \frac{f_s}{N_F}
\end{align}
$$

ここで、\(f_s\) はサンプリング周波数、\(\ N_F\) はFFT点数です。

ただし、k=0 または k=n_bin-1（一番大きい周波数ビン番号） のときは、

$$
r_1 = |X[k,i]|
$$

k'=0 または k'=n_bin-1 のときは、

$$
r_2 = |X[k',i]|
$$

また、peak_plane[k,i] == BIRTH または peak_plane[k,i] == DEATH_BIRTH のときは、

$$ r_1 = 0 $$

peak_plane[k',i] == DEATH または peak_plane[k',i] == DEATH_BIRTH のときは、

$$ r_2 = 0 $$

とします。

その後、ピークごとにフレーム間の信号を再合成します。

ピークのインデックスを\(\ p\ \)とすると、プレーム間の各正弦波モデルの振幅\(\ A_p[n]\) は以下のように線形補間で求めます。

$$
A_p[n] = r_1 + frac{r_2 - r_1}{S} n \hspace{1em}(n=0,1,\cdots, S-1)
$$

ここで、\(S \) はフレームシフト点数です。

フレーム間の各信号の位相\(\ \theta_p[n]\) は以下のように３次補間で求めます。

$$
\theta_p[n] = \theta_1 + \omega_1 \frac{n}{f_s} + \alpha (M) \left(\frac{n}{f_s}\right)^2 + \beta (M) \left(\frac{n}{f_s}\right)^3 \hspace{1em}(n=0,1,\cdots, S-1)
$$
$$
\begin{equation}
\begin{bmatrix}
\alpha(M)\\
\beta(M)
\end{bmatrix} =
\begin{bmatrix}
\frac{3}{T^2} & \frac{-1}{T}\\
\frac{-2}{T^3} & \frac{1}{T^2}
\end{bmatrix}
\begin{bmatrix}
\theta_2 -\theta_1-\omega_1 T + 2\pi M\\
\omega_2-\omega_1
\end{bmatrix}
\end{equation}
$$

\(M\ \)については以下のように求めます。

$$
M = {\rm round} \left( \frac{1}{2\pi} \left[(\theta_1+\omega_1 T - \theta_2) + (\omega_2 - \omega_1)\frac{T}{2}\right] \right)
$$

\(A_p[n]\) と \(\theta_p[n]\) を求めたら、再合成信号 \(y[n]\) を以下の式で求めます。

$$
y[n] = \sum_{p} A_p[n] \cos{(\theta_p[n])}
$$

プログラムの実行

プログラム中のパラメータを表のように設定して、プログラムを実行しました。

パラメータ名 記号 変数名 設定値
サンプリング周波数 (f_s) sr_o 10 kHz
FFT点数 (N_F) n_fft 512
フレームシフト点数 (S) hop_length 256
接続先の周波数範囲 (Delta f) delta_freq 50 Hz
窓関数 (w) window ハミング窓

プログラムの実行は記述したスクリプトmain.pyと音声ファイルvoice.wavを同じフォルダに置き、以下のようにして実行できます。

python main.py

歌声を再合成した結果は以下のようになります。

10kHz にリサンプリング後の歌声

正弦波モデルで再合成した歌声

かなりノイズがありますので、改善の余地がありそうですね。

おわりに

今回は正弦波モデルを実装しました。論文では、窓関数の幅を基本周波数に応じて変えたり、1フレームの最大ピーク数を決めていたりしているので、それらを実装することでさらに良質な歌声を再合成できるかもしれません。

参考文献
[1] 小坂 直敏、「サウンドエフェクトのプログラミング―Cによる音の加工と音源合成」、オーム社、2012.
[2] R.J.McAulay and T.F.Quatieri , “Speech Analysis/Synthesis Based on a Sinusoidal Representation”, IEEE Trans. on Acoust., Speech, and Singnal Processing, vol. ASSP-34, No. 4, Aug. 1986.

使用した楽曲について
この記事で信号処理した楽曲は Pixabay で提供されている Lifeisnurul の Heartbeat's Symphony を使用させていただきました。
【楽曲情報】
"Heartbeat's Symphony" 2024 Lifeisnurul (Public Domain)