２分割のフィルタバンクについてまとめてみました。
実用的なフィルタバンクである2チャンネルのQMFバンク（直交ミラーフィルターバンク：Quadrature Mirror Filter Bank）の実装を通して、フィルタバンクについてまとめていきます。
フィルタバンクとは
参考文献[1]にはフィルタバンクについて以下のような記載があります。
フィルタバンク
フィルタバンクとは，複数個のフィルタにより構成され、全体としてある機能の持つシステムの総称である。
引用元：貴家仁志, 「マルチレート信号処理 ディジタル信号処理シリーズ 第14巻」, 株式会社昭晃堂, 1995, p.89.
フィルタバンクの代表例としては以下のような構成があります。
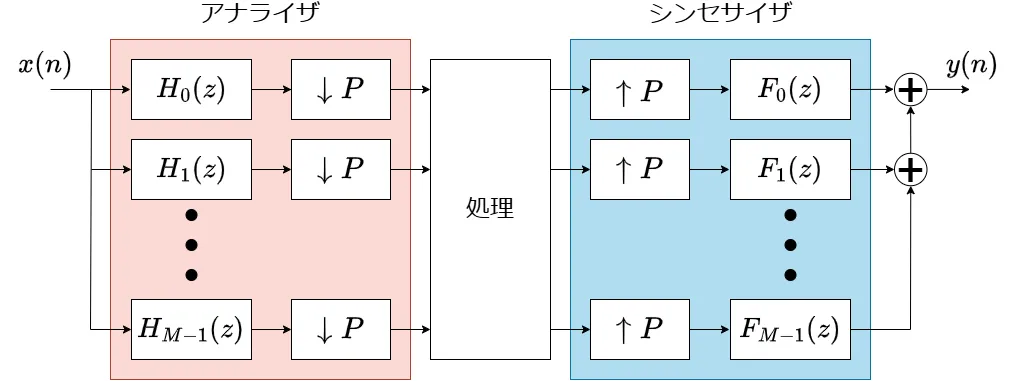
ここで、\(↓P\ \)はデシメータ、\(↑P\ \)はインタポレータである（詳細は後述）。
上図のシステムは信号\(x(n)\)をM個の帯域に分割後、デシメータによってサンプリングレートを下げて、処理を施しています。また、帯域ごとに処理した信号を足し合わせてもとの信号を合成することを想定しています。
このようなフィルタバンクではFFT等の他の周波数解析とは違い、解析後のデータ量が増えないという利点があります。
そのため、フィルタバンクは音声符号化で使われることが多い印象です。
以下ではフィルタバンクの各要素について説明いたします。
ダウンサンプラ
ダウンサンプラの処理手順は以下です。
- デシメータのエイリアシングを回避するために入力信号を帯域制限する。
- 帯域制限された信号をD個間隔で取り出す（デシメーション）。
エイリアシングの回避
デシメータではサンプリングレートを下げるため、エイリアシングが生じてしまいます。エイリアシングを回避するため、あらかじめ折り返される帯域をカットしておきます。
デシメータ
デシメータ（\(↓D\ \)）は信号をＤ個間隔で取り出す操作となります。
数式で表現すると以下です。
$$
y[m]=v[Dm]
$$
z変換すると以下になります。
$$
\begin{align}
Y(z)&=\sum_{m=-\infty} v[Dm]z^{-m} \\
&= \frac{1}{D}\sum_{k=0}^{D-1} V(W^{k}z^{1/D}) \tag{*}
\end{align}
$$
ここで、\(W=\exp(-j2\pi / D)\ \) です。
周波数領域では以下となります。
$$
Y(\omega)=\frac{1}{D}\sum_{k=0}^{D-1} V\left(\frac{\omega-2\pi k}{D} \right)
$$
振幅特性をグラフで表すとx軸方向にD倍拡大されて、y軸方向に1/D倍縮小されたグラフになります。
デシメーションのz変換：(*)式の求め方を補足します。
まず、インパルス列\(\ p[n]\ \) と入力信号\(\ v[n]\ \)の掛け算を計算します。
\(p[n]\ \)については離散フーリエ級数展開によって以下のように表せます。
$$
\begin{align}
p[n] &= \frac{1}{D}\sum_{k=0}^{D-1}P[k]e^{j2\pi kn/D} \\
&= \frac{1}{D}\sum_{k=0}^{D-1}1 \cdot e^{j2\pi kn/D} \\
&= \frac{1}{D}\sum_{k=0}^{D-1}e^{j2\pi kn/D}
\end{align}
$$
\(P[k]\) はフーリエ係数の求め方から以下のように計算しています。
$$
\begin{align}
P[k] &= \sum_{n=0}^{D-1} p[n]e^{-j2\pi kn/D} \\
&= p[0] \cdot e^{-j2\pi k 0/D} \\[5pt]
&= 1
\end{align}
$$
以上より、インパルス列の掛け算のz変換は以下となります。
$$
\begin{align}
& \sum_{n=-\infty}^{\infty} p[n]v[n] z^{-n} \\
=& \sum_{n=-\infty}^{\infty} \left(\frac{1}{D}\sum_{k=0}^{D-1} e^{j2\pi kn/D}\right) v[n] z^{-n} \\
=& \frac{1}{D} \sum_{k=0}^{D-1} \left(\sum_{n=-\infty}^{\infty} v[n] (e^{-j2\pi k/D} z)^{-n}\right) \\
=& \frac{1}{D} \sum_{k=0}^{D-1} V(e^{-j2\pi k/D}z)
\end{align}
$$
したがって、\(p[n]=0\ (n\neq Dm)\ \)より
$$
\begin{align}
Y(z) =& \sum_{m=-\infty}^{\infty} p[Dm]v[Dm] z^{-m} \\
=& \sum_{n=-\infty}^{\infty} p[n]v[n] z^{-n/D} \\
=& \frac{1}{D} \sum_{k=0}^{D-1} V(e^{-j2\pi k/D}z^{1/D})
\end{align}
$$
計算効率化
上記の計算でダウンサンプリングが可能ですが、この方法を実直に行った場合、計算に無駄があります。
以下の青い値はデシメーションによって間引かれるため、フィルタの出力を計算する必要がありません。
そこで、以下のようにデシメーション後にフィルタの畳み込みを計算します。
\begin{align}
y[m] &= \sum_{l=0}^{\infty} h[l]x[Dm-l] \\
&= \sum_{i=0}^{D-1} \left(\sum_{l=0}^{\infty} h[Dl+i]x[Dm-(Dl+i)] \right)
\end{align}
$$
ブロック図で表すと以下です。
ここで、\(E_{i}(z)\ \)は伝達関数\(\ H(z)\ \)を以下のように分解したフィルタです。
\begin{align}
H(z) &= \sum_{n=-\infty}^{\infty} h[n]z^{-n} \\
&= \sum_{i=0}^{D-1} \left(\sum_{l=-\infty}^{\infty}h[Dl+i]z^{-Dl}\right) z^{-i} \\
&= \sum_{i=0}^{D-1} E_{i}(z^{D})z^{-i} \\
\Bigl(E_{i}(z) &= \sum_{l=-\infty}^{\infty}h[Dl+i]z^{-l}\Bigr)
\end{align}
$$
この伝達関数の表現をタイプⅠのポリフェーズ表現といい、\(E_{i}(z)\ \)は\(\ H(z)\ \)のポリフェーズフィルタといいます。
アップサンプラ
アップサンプラの処理手順は以下です。
- 各信号間にU-1個のゼロ値を挿入する（インタポレーション）。
- インタポレーションによるイメージング成分をフィルタで除去する。
インタポレータ
時間領域において、インタポレータ（\(↑U\ \)）は各信号間にU-1個のゼロ値を挿入する操作となります。
これを数式で表すと以下になります。
w[n] =
\begin{cases}
x[n/U], & n=0, \pm U, \pm 2U, \cdots \\[5pt] 0, & {\rm otherwise}
\end{cases}
$$
z変換すると以下になります。
\begin{align}
W(z) &= \sum_{n=-\infty}^{\infty} w[n]z^{-n} \\
&= \sum_{m=-\infty}^{\infty} w[mU]z^{-mU} \\
&= \sum_{m=-\infty}^{\infty} x[m]z^{-mU} \\[5pt] &= X(z^{U})
\end{align}
$$
周波数領域では以下となります。
$$
W(\omega) = X(U\omega)
$$
振幅特性をグラフで表すとx軸方向に1/U倍縮小されたグラフになります。
イメージング成分の除去
インタポレーションによってイメージング成分が生じているため、これを下図のようにフィルタによって除去します。
計算効率化
アップサンプリングについても計算を効率化する方法があります。
以下の赤い値はゼロであるため、計算する必要がありません。
そこで、以下のようにアップサンプリング前に畳み込みを計算します。
y[Um+i] = \sum_{l=0}^{\infty} f[Ul+i]x[m-l] $$
ここで、\(i=0,1,\cdots,U-1\) です。
ブロック図で表すと以下です。
ここで、\(R_{i}(z)\) は伝達関数\(\ F(z)\ \)を以下のように分解したフィルタです。
\begin{align}
F(z) &= \sum_{n=-\infty}^{\infty} f[n]z^{-n} \\
&= \sum_{i=0}^{U-1} \left(\sum_{l=-\infty}^{\infty}f[Ul+(U-1-i)]z^{-Ul}\right) z^{-(U-1-i)} \\
&= \sum_{i=0}^{U-1} R_{i}(z^{U})z^{-(U-1-i)} \\
\Bigl(R_{i}(z) &= \sum_{l=-\infty}^{\infty}f[Ul+(U-1-i)]z^{-l}\Bigr)
\end{align}
$$
この伝達関数の表現をタイプⅡのポリフェーズ表現といい、\(R_{i}(z)\ \)は\(\ F(z)\ \)のポリフェーズフィルタといいます。
タイプⅠとタイプⅡの分解についての違いはほとんどなく、単純に以下の関係があるだけです。
$$
R_{i}(z) = E_{U-1-i}(z)
$$
2CHの完全再構成条件
本記事では、下図の2分割フィルタバンクの再構成条件について考えます。
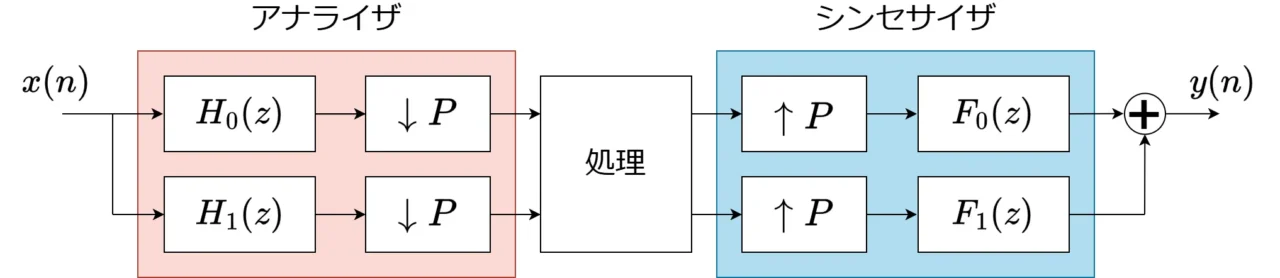
設計条件
処理ブロックがない場合、2分割フィルタバンクの入力と出力の関係は以下のように書けます。
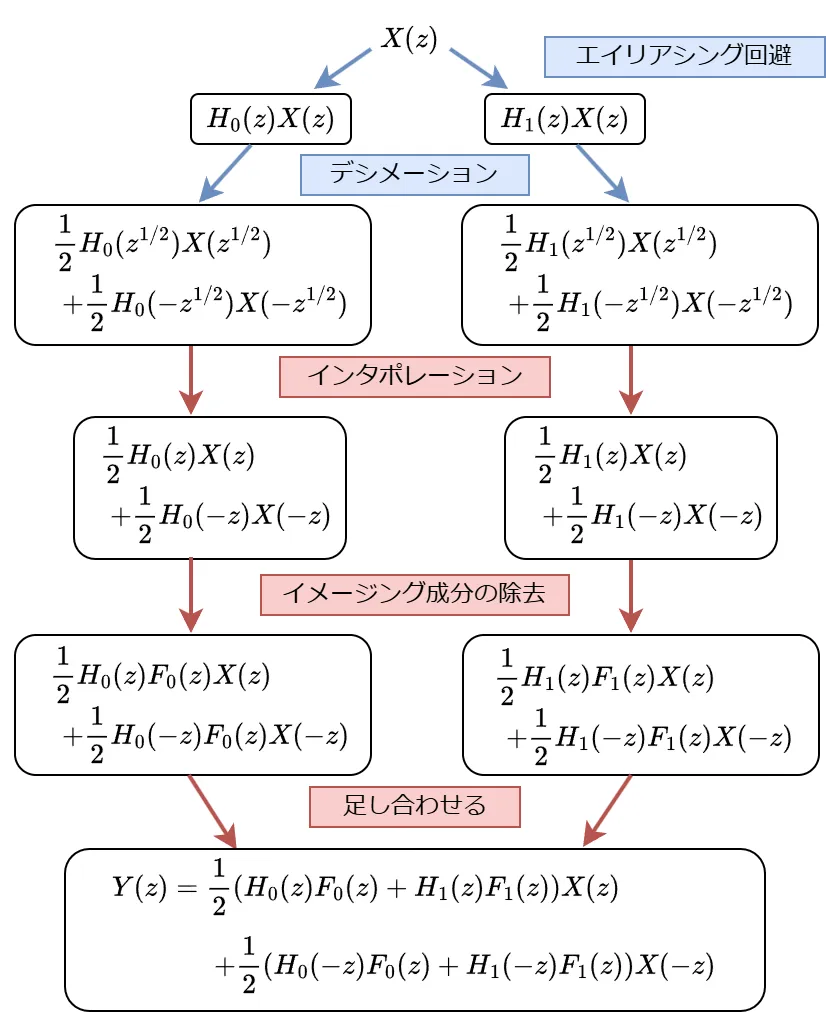
入力信号を再構成するには入力と出力の関係が以下のようになれば良いです。
$$
Y(z)=z^{-L}X(z)
$$
ここで L は整数です。時間領域では \(\ y(n)=x(n-L)\ \) となり、要は遅延があるだけならばよいです。
2分割フィルタの入出力関係が遅延だけになるには以下の2つの条件を満たせばよいです。
\begin{align}
H_{0}(-z)F_{0}(z)+H_{1}(-z)F_{1}(z) = 0 \tag{A} \\[5pt] H_{0}(z)F_{0}(z)+H_{1}(z)F_{1}(z) = 2z^{-L} \tag{B}
\end{align}
$$
エイリアシングの除去条件
(A)式がデシメーションやインタポレーションで生じる成分（エイリアシング成分、イメージング成分）を除去する条件式です。
(A)式については、シンセサイザフィルタを以下のように作成することで満たせます。
$$
\begin{align}
F_{0}(z)&=H_{1}(-z) \tag{C} \\[5pt]
F_{1}(z)&=-H_{0}(-z) \tag{D}
\end{align}
$$
オールパス条件
(C)式と(D)式を適用することで(B)式は以下のようになります。
H_{0}(z)H_{1}(-z)-H_{1}(z)H_{0}(-z) = 2z^{-L}
$$
\(H(z)=H_{0}(z)H_{1}(-z)\) とおけば、以下のように表現できます。
$$
H(z)-H(-z) = 2z^{-L} \tag{E}
$$
(E)式を満たすには、\(H(z)\) のインパルス応答\(\ h[n]\ \)が以下であればよい。
- インパルス応答の個数\(M\)が奇数、かつ\(\ (M-1)/2\ \)も奇数である。
- \(\ L=(M-1)/2\ \)を除き、奇数番目の\(\ h[n]\ \)はゼロ値である。
例としては以下のような\(\ M=11\ \)のインパルス応答となります。
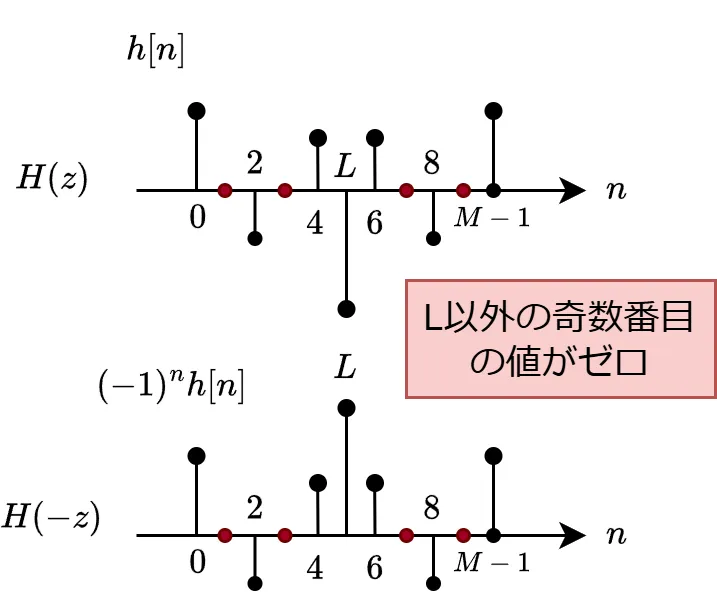
\(H(z)\)が上記の条件を満たすように \(H_{0}(z), H_{1}(z)\) を設計していきます。設計方法についてはいくつかあります。
QMFバンク
\(H_{0}(z), H_{1}(z)\) の設計方法の一つにQMFバンクがあります。QMFバンクは1977年に D.Esteban によって報告されたフィルタバンクです。
QMFバンクの特徴
QMFバンクの特徴は以下となります。
- (A)式のエイリアシングの除去条件を満たす。
- (B)式のオールパス条件を近似的に満たす（例外あり）。
- 各フィルタは直線位相特性を持つ。
QMFバンクでは、アナライザフィルタが以下の関係を持つように設計します。
$$
H_{1}(z)=H_{0}(-z) \tag{F}
$$
以上の関係よりシンセサイザフィルタは以下のようになります。
$$
\begin{align}
F_{0}(z)&=H_{0}(z) \\[5pt]
F_{1}(z)&=-H_{0}(-z)
\end{align}
$$
このとき、オールパス条件(E)式の\(\ H(z)\ \)は以下となります。
$$
H(z)=H_{0}(z)^2 \tag{G}
$$
オールパス条件
オールパス条件(E)式とQMFの条件(F)式を同時に満たす\(\ H_0(z)\ \)を考えていきます。
\(H_0(z)\ \)はタイプⅠのポリフェーズ表現より以下のように表せます。
$$
H_0(z) = E_0(z^2) + z^{-1}E_{1}(z^2)
$$
(E)式の左辺はこのとき、
\begin{align}
& H(z)-H(-z) \\[5pt] =\ & H_{0}(z)^2 - H_{0}(-z)^2 \\[5pt] =\ & E_{0}(z^2)^2 + 2z^{-1}E_{0}(z^2)E_{1}(z^2) + z^{-2}E_{1}(z^2)^2 \\[2pt] \ &-(E_{0}(z^2)^2 - 2z^{-1}E_{0}(z^2)E_{1}(z^2) + z^{-2}E_{1}(z^2)^2) \\[5pt] =\ & 4z^{-1}E_0(z^2)E_{1}(z^2)
\end{align}
$$
となるため、(E)式の右辺となるにはポリフェーズフィルタが以下である必要がある。
$$
\begin{align}
E_{0}(z^2) &= c_{0}z^{-2n_{0}} \\[5pt]
E_{1}(z^2) &= c_{1}z^{-2n_{1}}
\end{align}
$$
ここで、\(c_0, c_1\ \)は任意の定数であり、\(n_0, n_1\ \)は整数である。
このとき、
$$
H_{0}(z) = c_{0}z^{-2n_{0}} + c_{1}z^{-(2n_{1}+1)}
$$
したがって、(E)式かつ(F)式を満たす次数の大きい\(\ H_0(z)\ \)の作成はできないため、(E)式を近似的に満たすフィルタを設計する必要がある。
ちなみに、(E)式かつ(F)式を満たすフィルタには以下のハールフィルタ(Haar Filter)がある[2]。
$$
H_{0}(z) = \frac{1+z^{-1}}{\sqrt{2}}
$$
フィルタの制約
フィルタ\(\ H_{0}(z)\ \)のインパルス応答には制約があり、下図のようにインパルス応答が偶対称であり、個数M（タップ長）が偶数の直線位相フィルタである必要があります。
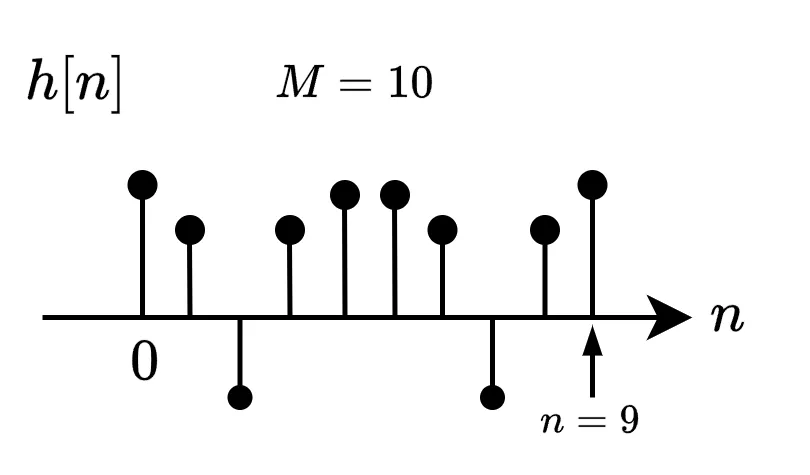
偶対称である必要性としては、インパルス応答が奇対称ではローパスフィルタを作成できないためです。
偶数個である必要性としては、奇数個のインパルス応答では(E)式を近似的に満たせないからです。
線形位相フィルタの場合、周波数特性は以下のように表せます。
$$
H_{0}(\omega) = e^{-j\omega \frac{(M-1)}{2}}|H_{0}(\omega)|
$$
このとき、\(\omega\)で表現した(E)式の左辺は以下となります。
\begin{align}
& H(\omega)-H(\pi-\omega) \\[5pt] =\ & H_{0}(\omega)^2 - H_{0}(\pi-\omega)^2 \\[5pt] =\ & e^{-j\omega (M-1)} \left(|H_{0}(\omega)|^2 - (-1)^{(M-1)}|H_{0}(\pi-\omega)|^2 \right)
\end{align}
$$
Mが奇数の場合、\(\omega=\pi/2\) のとき、上式が０となってしまうため、個数 M は偶数の必要があります。
設計方法
フィルタ\(\ H_0(z)\ \)はいくつか設計方法があるようですが、本記事ではJ.D.Jhonston らの方法を使用したいと思います[3]。
J.D.Jhonston らは以下の目的関数\(\ E\ \)を最小化する\(\ H_0(\omega)\ \)を探索しました。
\begin{align}
E &= E_{r} + \alpha E_{s} \\[5pt] \biggl(E_r &= 2\int_{0}^{\pi/2}(|H_{0}(\omega)|^{2}+|H_{0}(\pi-\omega)|^{2}-1)^2 {\rm d\omega} \biggr) \\[5pt] \biggl(E_s &= \int_{\omega_{SB}}^{\pi} |H_{0}(\omega)|^{2} {\rm d\omega} \biggr)
\end{align}
$$
ここで、\(\alpha\ \)は阻止域の重み係数、\(\omega_{SB}\ \)は阻止域端角周波数である。
探索の方法としては、Hooke and Jeeves 法を使用します。
Hooke and Jeeves 法による手順は以下です[4]。
- 初期値 \(h[n]^{(0)}\) と 初期探索幅 \(\Delta\) をセットする
- \(n=0\ \)とする
- \(h[n]^{(k)}\leftarrow h[n]^{(k)}+\Delta\)で目的関数を評価
- 目的関数が改善していたら、値を採用して、\(k\leftarrow k+1\)、\(\ n\leftarrow n+1\)
改善していなかったら、値を不採用して、\(\Delta\leftarrow -\Delta\) で目的関数を再評価これで改善していたら、値を採用して、\(k\leftarrow k+1\)、\(\ n\leftarrow n+1\)
これでも改善しなかったら、値を不採用して、\(\ n\leftarrow n+1\) だけする - \(n < M/2 \ \)のときは３に戻る、違う場合は６に進む
- 探索によって改善した場合、再度２へ戻る。改善しない場合は\(\Delta\leftarrow \rho\Delta\) で２へ戻る。\(\Delta\)が所定の基準値より小さくなったらアルゴリズム終了
単純な方法ですが、目的関数の勾配を計算する必要がないため、最小化するパラメータが少ないときに現在でも使用されているアルゴリズムです。
プログラム
QMFバンクのフィルタを求めるプログラムをPythonで実装しました。ソースコードと実行方法について説明します。
ソースコード
2CHのQMFバンクのフィルタを求めるプログラムは以下です。
import numpy as np
import scipy.signal as sg
import matplotlib.pyplot as plt
# パラメータ
tr_band = 2*np.pi*0.0625 # 遷移域の幅
omega_sb = np.pi/2 + tr_band # 阻止域端角周波数
alpha = 2 # 重み係数
M = 48 # タップ長
delta = 0.1 # 初期探索幅
delta_min = 10**(-8) # 探索幅の下限
rho = 0.2 # 探索幅の変化量
N_FFT = 512 # H0のFFT点数
#############################################
# 目的関数を計算する
# h: フィルタ係数
#############################################
def calculate_E( h ):
global N_FFT
global alpha
global omega_sb
# 周波数特性を求める
freq, H_0 = sg.freqz(h, whole=True, worN=N_FFT)
## Er を求める
Er = 0.0
for k in range(N_FFT):
if freq[k] < np.pi/2.0 :
Er += 2.0*(np.abs(H_0[k])**2+ \
np.abs(H_0[N_FFT//2-k])**2-1.0)**2
## Es を求める
Es = 0.0
for k in range(N_FFT):
if omega_sb < freq[k] and freq[k] < np.pi:
Es += np.abs(H_0[k])**2
## E を求める
E = Er + alpha*Es
return E
#############################################
# 1回探索作業する
# h: フィルタ係数
# pre_E: 前回の目的関数の値
#############################################
def search_filterCoef(h, pre_E):
global M
global delta
global k
for n in range( M//2 ):
# h[n] ← h[n]+Δ
h_tmp = h[n]
h[n] = h[n] + delta
h[M-1-n] = h[n]
# 目的関数を計算
E = calculate_E(h)
# 改善していたら、値を採用
if E < pre_E:
k = k + 1
pre_E = E
# 改善していなかったら、値を不採用で再評価
else:
# h[n] ← h[n]-Δ
h[n] = h_tmp
h[n] = h[n] - delta
h[M-1-n] = h[n]
# 目的関数を計算
E = calculate_E(h)
# 改善していたら、値を採用
if E < pre_E:
k = k + 1
pre_E = E
# 改善していなかったら、値を不採用
else:
h[n] = h_tmp
h[M-1-n] = h_tmp
return (pre_E, h)
### Hooke and Jeeves 法 ###
# 初期化
## 窓関数法によって作成したフィルタを初期値とする
h = sg.firwin(numtaps=M, cutoff=omega_sb-0.03, \
width=None, window='hann', fs=2*np.pi)
k = 0
pre_E = 10**10 # 大きな値を入れて必ず更新されるようにする
# Δが所定の基準値より小さくなったらアルゴリズム終了
while delta > delta_min:
# 探索する
E, h = search_filterCoef(h, pre_E)
# 改善した場合
if pre_E > E:
pre_E = E # 値を保存
# 改善しない場合
else:
delta = rho*delta # 探索幅を更新
# 探索ごとに目的関数を表示
print( pre_E )
# 周波数特性
freq, H0 = sg.freqz(h)
H_amp = 20 * np.log10(np.abs(H0))
# 参考として[3]の論文のフィルタ特性を求める
h_tmp = [ 0.46424160 , 0.13207910, -0.99384370e-1, -0.43596380e-1, 0.54326010e-1, 0.18809490e-1, -0.34090220e-1, -0.78016710e-2, \
0.21736090e-1, 0.24626820e-2, -0.13441620e-1, -0.61169920e-4, 0.78402940e-2, -0.75614990e-3, -0.42153860e-2, 0.78333890e-3, \
0.20340170e-2, -0.52055750e-3, -0.85293900e-3, 0.24225190e-3, 0.30117270e-3, -0.56157570e-4, -0.92054790e-4, -0.14619070e-4]
h_jd = np.zeros(M)
h_jd[M//2:] = h_tmp
h_jd[0:M//2] = h_tmp[::-1]
freq, H_jd = sg.freqz(h_jd)
H_jdamp = 20 * np.log10(np.abs(H_jd))
#figオブジェクトを作成
fig = plt.figure(figsize = (8,6))
#グラフを描画するsubplot領域を作成
ax1 = fig.add_subplot(2, 1, 1)
ax2 = fig.add_subplot(2, 1, 2)
#各subplot領域にデータを渡す
ax1.plot(freq, H_amp, color="tab:blue")
ax1.plot(freq, H_jdamp, color="tab:orange")
ax2.plot(h, color="tab:blue")
ax2.plot(h_jd, color="tab:orange")
# x 軸のラベルを設定する。
ax1.set_xlabel("ω [rad]")
ax2.set_xlabel("n [sample]")
# y 軸のラベルを設定する。
ax1.set_ylabel("|H(ω)| [dB]")
ax2.set_ylabel("h[n]")
# インパルス応答とF特を出力
print(h)
plt.savefig("ftoku.png") # グラフ保存15～44行目：目的関数を計算する関数です。
25～26行目：文献[3]で512点のFFTを使って、周波数特性を計算したと書かれていたため、同じように512点FFTを計算しています。
46～90行目：Hooke and Jeeves法の2～5を実施する関数です。
60～62行目：インパルス応答を更新しています。QMFバンクのフィルタは偶対称のため、対称のフィルタ係数も更新しています。
92～115行目：Hooke and Jeeves法でQMFバンクのフィルタを求めています。
94～96行目：インパルス応答の初期値は窓関数法によって作成したフィルタ係数にしています。使用した窓関数はハン窓です。（上手く読み取れなかったですが、文献[3]も同じやり方だと思います。）
117～154行目：インパルス応答と周波数特性のグラフを出力しています。
121～129行目：参考として文献[3]に記載のフィルタの周波数特性も求めています。
実行方法
(1) プログラムを実行するディレクトリにソースコード(qmf.py)を格納する。
(2) ソースコード5～13行目のパラメータを変更する。
# パラメータ
tr_band = 2*np.pi*0.0625 # 遷移域の幅
omega_sb = np.pi/2 + tr_band # 阻止域端角周波数
alpha = 2 # 重み係数
M = 48 # タップ長
delta = 0.1 # 初期探索幅
delta_min = 10**(-8) # 探索幅の下限
rho = 0.2 # 探索幅の変化量
N_FFT = 512 # H0のFFT点数
(3) 以下のコマンドで python を実行することで、インパルス応答と周波数特性のグラフ ftoku.png が出力される。
$ python qmf.py
処理結果
下記のパラメータでフィルタを作成いたしました。探索幅の下限を小さくしたため、実行終了までに1時間くらいかかりました。
| パラメータ名 | 記号 | 変数名 | 設定値 |
|---|---|---|---|
| 遷移域の幅 | - | tr_band | \(2\pi\times 0.625\) |
| 阻止域端角周波数 | \(\omega_{SB}\) | omega_sb | \(\pi/2+2\pi\times 0.625\) |
| 重み係数 | \(\alpha\) | alpha | 2 |
| タップ長 | M | M | 48 |
| 初期探索幅 | \(\Delta\) | delta | 0.1 |
| 探索幅の下限 | - | delta_min | 10^(-8) |
| 探索幅の変化量 | \(\rho\) | rho | 0.2 |
| F特計算時のFFT点数 | - | N_FFT | 512 |
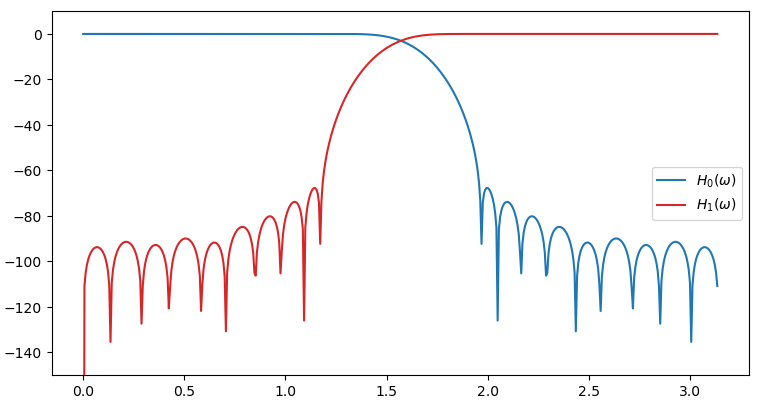
作成したフィルタの周波数特性は以下になります。論文[3]で同じような条件で作成したフィルタの特性も載せています（論文には探索幅のパラメータ値の記載がない）。
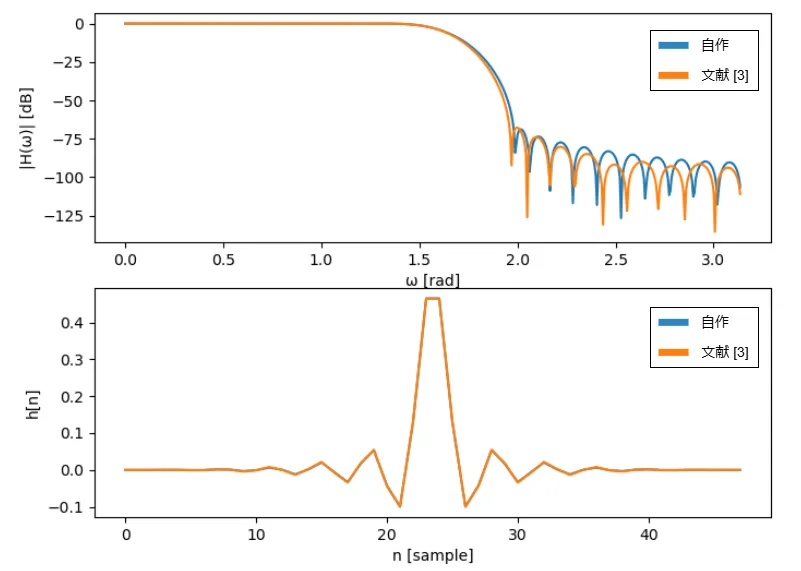
ターミナルに出力されたフィルタ係数は以下でした。
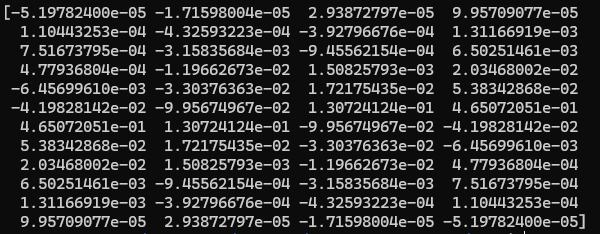
おわりに
本記事ではQMFバンクの実装を通して2分割フィルタバンクについてまとめました。フィルタバンクについて書かれた文献が1990年代のものしかなかったので、調べるのに苦労しましたが、この記事がフィルタバンクを学ぶことに対する敷居を下げていれば幸いです。
次はM分割フィルタかMP3のフィルタバンクについて書こうかなと思います。
■参考文献
[1] 貴家仁志, 「マルチレート信号処理 ディジタル信号処理シリーズ 第14巻」, 株式会社昭晃堂, 1995．
[2] Wikipedia, “直交ミラーフィルタ”, https://ja.wikipedia.org/wiki/直交ミラーフィルタ, (参照2024-12-29).
[3] J.D.Johnston, "A filter Family Designed for Use in Quadrature Mirror Filter Banks," IEEE Proc.ICASSP, pp.291-294, 1980.
[4] 宮田 悟志, Hooke-Jeeves パターン探索法のヒューリスティックな性能向上, 設計工学・システム部門講演会講演論文集, 2017, 2017.27 巻, p.2109, 公開日 2018/03/25.
■変更履歴
・2025/01/11：誤字の修正