Pythonでスペクトログラムの表示(scipy signal ShortTimeFFT)

scipy signal ShortTimeFFT クラスを使用したスペクトログラム表示について紹介します。

私自身はいままで scipy signal stft を使用していましたが、stft については今後アップデートはされないようです[1]。そのため、私もこれを機にShortTimeFFTを使用したいと思います。

1 ShortTimeFFT について
2 パラメータと返り値
3 主な使用例
4 ShortTimeFFT のパラメータ詳細
- 4.1 fft_mode
- 4.2 scale_to
5 spectrogram のパラメータ詳細
- 5.1 padding
- 5.2 その他のパラメータ
6 scale_to と fft_mode の設定
- 6.1 scale_to の設定
- 6.2 fft_mode の設定
7 おわりに

ShortTimeFFT について

scipy signal ShortTimeFFT は SciPy v1.12.0 で提供された新しいクラスです。

scipy signal ではスペクトログラム表示のための関数として stft や spectrogram を提供していましたが、Scipy v1.12.0 以降はレガシーとなり、今後はアップデートされないみたいです。

ShortTimeFFT のメソッドに spectrogram というスペクトログラムを表示するものがあるため[2]、それを使用していきたいと思います。

パラメータと返り値

scipy signal ShortTimeFFT クラスのパラメータは以下です（他にもパラメータありますが、スぺクトログラム表示に関連するものだけ紹介します）。

scipy.signal.ShortTimeFFT(win, hop, fs, fft_mode='onesided', mfft=None, scale_to=None)

表：scipy.signal.ShorTimeFFTのパラメータ
パラメータ名	データ型	概要
win	np.ndarray	窓関数
hop	int	ホップサイズ
fs	float	サンプリングレート
fft_mode	str	スペクトログラムの出力方法
mfft	int	FFT点数
scale_to	str	窓関数の補正

スペクトログラムを求めるメソッド ShortTimeFFT spectrogram のパラメータは以下です。

ShortTimeFFT.spectrogram(x, p0=None, p1=None, k_offset=0, padding='zeros', axis=-1)

表：scipy.signal.ShorTimeFFTのパラメータ
パラメータ名	データ型	概要
x	np.ndarray	入力データ
p0	int	開始フレーム
p1	int	終了フレーム
k_offset	int	開始サンプル
padding	str	パディング方法
axis	int	STFTを計算する次元

主な使用例

スペクトログラムの表示（モノラル）

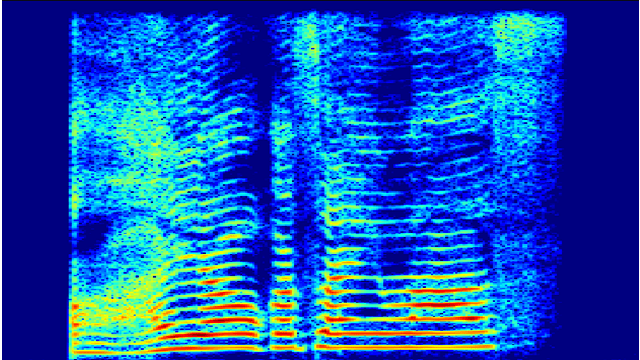
ShortTimeFFT を使用したスぺクトログラムを表示するソースコードは以下です。

import numpy as np
import soundfile as sf
import scipy.signal as sg
import matplotlib.pyplot as plt

# WAV を読み込む
x, fs = sf.read('input.wav')

# 窓関数作成
win = sg.windows.hann(512)  # 窓関数

# スぺクトログラム作成
SFT = sg.ShortTimeFFT(win, hop=128, fs=fs, \
                      fft_mode='onesided2X', \
                      scale_to='magnitude')
Sxx = SFT.spectrogram(x)
Sxx_dB = 10 * np.log10(np.fmax(Sxx, 1e-8))

# 時間軸と周波数軸の作成
N_t = np.arange(Sxx.shape[1])
t = SFT.delta_t * N_t
f = SFT.f

# グラフ作成
fig = plt.figure(figsize=(12,6))
plt.pcolormesh(t, f, Sxx_dB, cmap="jet")
plt.colorbar(label="Power [dbFS]")
plt.ylabel('Frequency [Hz]')
plt.xlabel('Time [sec]')
plt.savefig("spectrogram1.png")

基本的には sg.ShortTimeFFT に窓関数（win）、ホップサイズ（hop）、サンプリングレート（fs）を与えてクラスを作成して、SFT.spectrogram に入力データを与えるだけでスペクトログラムを作成できます。

FFT点数（mfft）については mfft=None であれば、窓関数 win のサイズに設定されます。

fft_mode, scale_to についてはあとで説明します。

作成されたスペクトログラムを以下に示します。

スペクトログラムの表示（ステレオ）

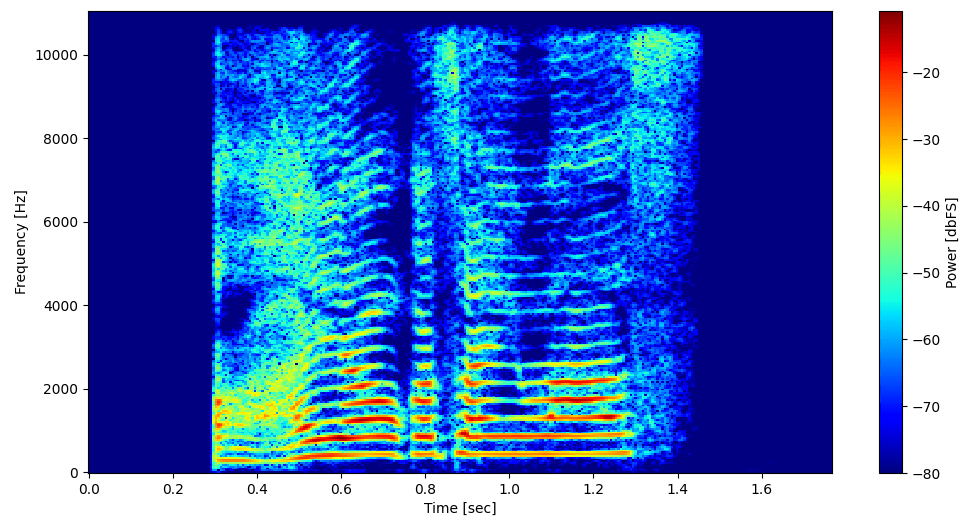
ステレオのスぺクトログラムを表示するソースコードは以下です。

import numpy as np
import soundfile as sf
import scipy.signal as sg
import matplotlib.pyplot as plt

# WAV を読み込む
x, fs = sf.read('input_stereo.wav')

# 窓関数作成
win = sg.windows.hann(512)  # 窓関数

# スぺクトログラム作成
SFT = sg.ShortTimeFFT(win, hop=128, fs=fs, \
                      fft_mode='onesided2X', \
                      scale_to='magnitude')
Sxx = SFT.spectrogram(x, axis=0)
Sxx_dB = 10 * np.log10(np.fmax(Sxx, 1e-8))

# 時間軸と周波数軸の作成
N_t = np.arange(Sxx.shape[2])
t = SFT.delta_t * N_t
f = SFT.f

# グラフ作成
fig = plt.figure(figsize=(12,8))
ax1 = fig.add_subplot(2, 1, 1)
ax2 = fig.add_subplot(2, 1, 2)
vmax=np.max(Sxx_dB)
vmin=np.min(Sxx_dB)
ax1.pcolormesh(t, f, Sxx_dB[:,0,:], cmap="jet", vmax=vmax, vmin=vmin)
ax2.pcolormesh(t, f, Sxx_dB[:,1,:], cmap="jet", vmax=vmax, vmin=vmin)
ax1.set_ylabel('Frequency [Hz]')
ax2.set_ylabel('Frequency [Hz]')
plt.xlabel('Time [sec]')
plt.savefig("spectrogram2.png")

ステレオの場合、SFT.spectrogram の axis にスペクトログラムを計算する信号の軸を与えます。sf.read の出力は（信号の長さ、チャンネル数）の多次元配列であるため、axis に 0 を与えます。

作成されたステレオのスペクトログラムを以下に示します。

スペクトログラムの比較

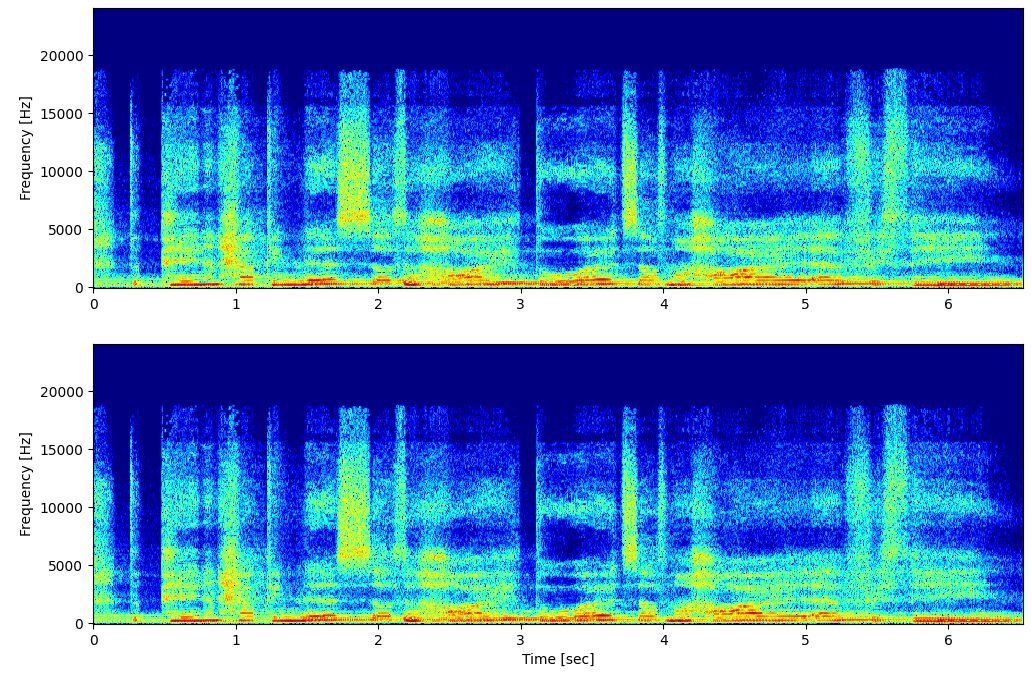
スペクトログラムを比較するソースコードは以下です。

import numpy as np
import soundfile as sf
import scipy.signal as sg
import matplotlib.pyplot as plt

# WAV を読み込む
x1, fs = sf.read('input1.wav')
x2, fs = sf.read('input2.wav')

# 窓関数作成
win = sg.windows.hann(512)  # 窓関数

# スぺクトログラム作成
SFT = sg.ShortTimeFFT(win, hop=128, fs=fs, \
                      fft_mode='onesided2X',\
                      scale_to='magnitude')
S1xx = SFT.spectrogram(x1)
S2xx = SFT.spectrogram(x2)
S1xx_dB = 10 * np.log10(np.fmax(S1xx, 1e-8))
S2xx_dB = 10 * np.log10(np.fmax(S2xx, 1e-8))

# 時間軸と周波数軸の作成
N_t = np.arange(S1xx.shape[1])
t = SFT.delta_t * N_t
f = SFT.f

# グラフ作成
fig = plt.figure(figsize=(12,8))
ax1 = fig.add_subplot(2, 1, 1)
ax2 = fig.add_subplot(2, 1, 2)
vmax=np.max(S1xx_dB)
vmin=np.min(S1xx_dB)
ax1.pcolormesh(t, f, S1xx_dB, cmap="jet", vmax=vmax, vmin=vmin)
ax2.pcolormesh(t, f, S2xx_dB, cmap="jet", vmax=vmax, vmin=vmin)
ax1.set_ylabel('Frequency [Hz]')
ax2.set_ylabel('Frequency [Hz]')
plt.xlabel('Time [sec]')
plt.savefig("spectrogram3.png")

スペクトログラムを１つ表示する場合とほとんど変わりません。ただし、信号を比較するために２つの pcolormesh に与える vmin と vmax は同じである必要があります。

作成されたスペクトログラムを以下に示します。

ShortTimeFFT のパラメータ詳細

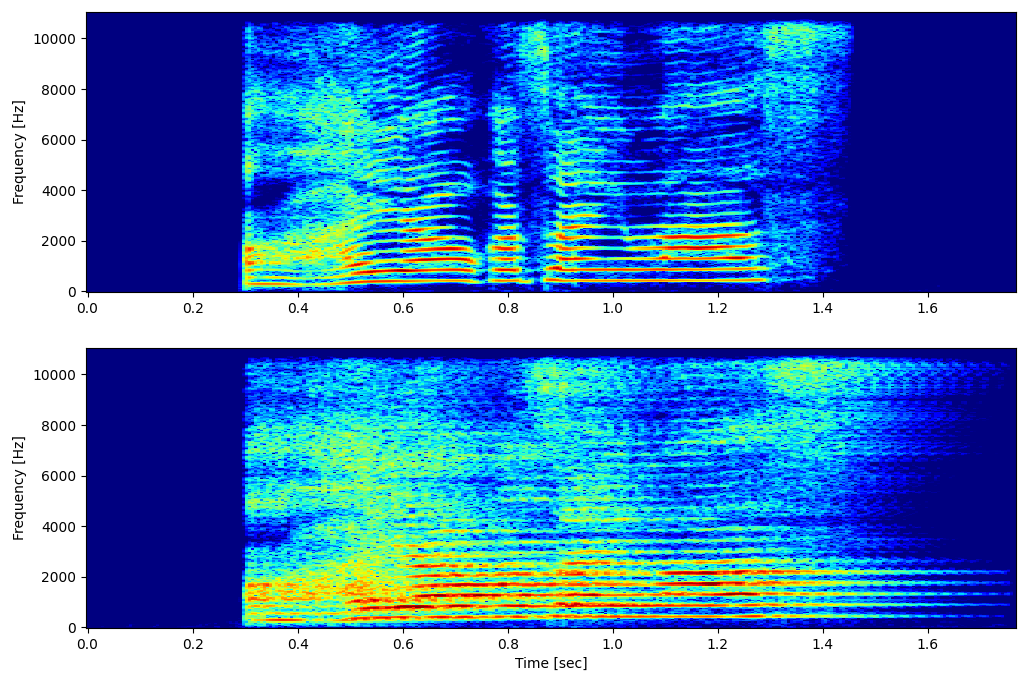
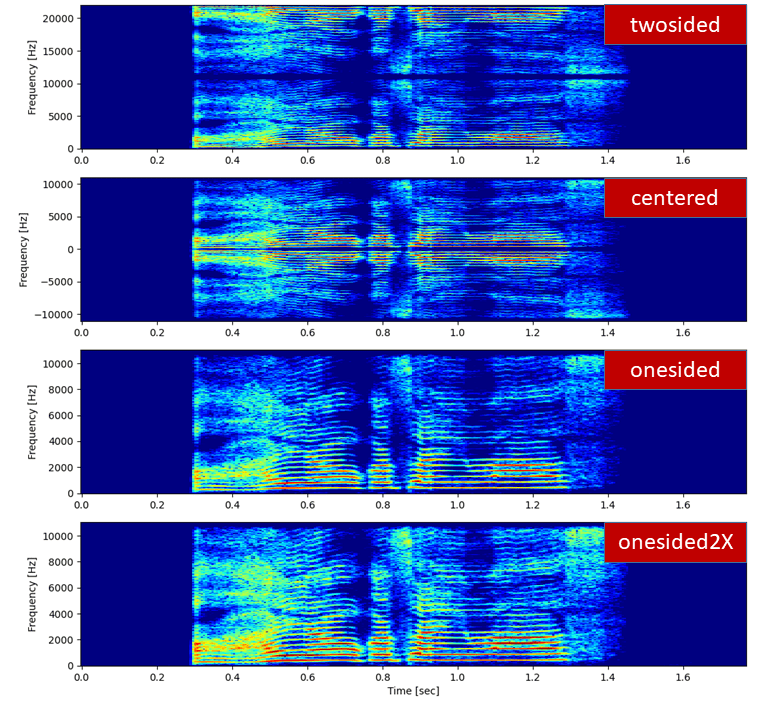
fft_mode

fft_mode には "twosided", "centered", "onesided", "onesided2X" があり、出力されるFFTの結果が変わります。以下の fs はサンプリング周波数です。

● twosided
0 [Hz] ～ fs [Hz]のスペクトログラムを出力するモード。

● centered
-fs/2 [Hz] ～ fs/2 [Hz]のスペクトログラムを出力するモード。

● onesided
0 [Hz] ～ fs/2 [Hz]のスペクトログラムを出力するモード。

● onesided2X
0 [Hz] ～ fs/2 [Hz]のスペクトログラムを出力するモード。また、0 以外の周波数成分の大きさがscale_to = "magnitude"のときは2倍、scale_to = "psd"のときは $\sqrt{2}$ 倍になる。

fft_modeを各モードに設定したときのスペクトログラムを以下に示します。

scale_to

scale_to には "magnitude", "psd" があります。

● magnitude
以下の補正した窓関数 w' を使用してスぺクトログラムを計算する。N は窓関数の大きさです。

$$
w'[n] = \frac{w[n]}{\sum_{n=0}^{N-1}w[n]}
$$

● psd
パワースペクトル密度（PSD）を計算する。

spectrogram のパラメータ詳細

padding

padding には "zeros", "edge", "even", "odd" があります。入力データ x の下端や上端でフレーム内にデータがないとき、追加される値を決定します。

● zeros
ゼロパディングを行います。

● edge
入力データ x の最初の値か最後の値でパディングされます。

● even
端で折り返したものでパディングされます。

● odd
端で折り返したものに -1 した値でパディングされます。

その他のパラメータ

p0

出力するスペクトログラムの開始フレーム番号

p1

出力するスペクトログラムの終了フレーム番号

k_offset

スぺクトログラムを求める開始サンプル番号

axis

スペクトログラムを計算する入力データ x の軸

scale_to と fft_mode の設定

主な使用例で scale_to="magnitude" と fft_mode="onesided2X"を使用した理由について説明します。

scale_to の設定

主な使用例で "magnitude" を使用した理由としては、窓関数を掛けた信号は小さくなってしまうので補正する必要があることと、スペクトログラムの値をわかりやすくするためです。

1. 窓関数を使用することで信号の大きさが (窓関数の合計値)/N 小さくなっているので、N/(窓関数の合計値)を掛けて補正します。

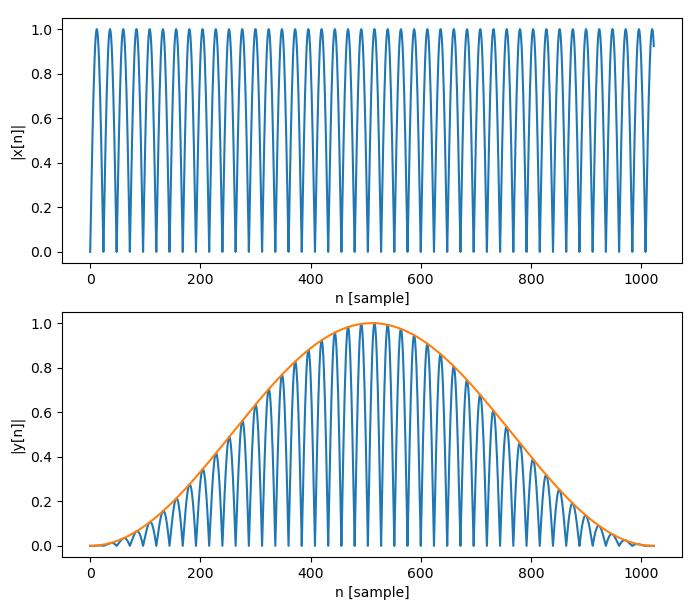
2. 信号 x[n] とFFT後の結果 X[k] は以下のような関係があります。

$$
x[n] = \frac{1}{N}\sum_{k=0}^{N-1} X[k] e^{j2\pi \frac{k}{N} n}
$$

例えば、$x[n]=\sin(2\pi n/N)$ のときは$X[1] = N/(2j)$ となり、窓関数の大きさ N によってスぺクトログラムの値が変わってしまいます。これは好ましくないため、あらかじめ 1/N で割っておきます。

以上から窓関数に 1/N * N/(窓関数の合計値)=1/(窓関数の合計値) を掛けてスペクトログラムを計算します。

fft_mode の設定

主な使用例で "onesided2X" を使用した理由としては、フルスケールの信号を入力したとき、その周波数成分が 0 dBFS になってほしかったからです。dBFS はフルスケールの信号を基準としたデジタル信号の大きさの単位です。

正弦波は以下のように複素正弦波で表せます。

$$
a \sin\left(2\pi\frac{k}{N}n\right) = a \frac{e^{j2\pi\frac{k}{N}n}-e^{-j2\pi\frac{k}{N}n}}{2j}
$$

"onesided" では複素正弦波 $ae^{j2\pi kn/N}/2j$ のパワーが出力されます。この場合、フルスケールの正弦波を入力したとき、スペクトログラムの値が -6 [dBFS] となってしまいます。

フルスケールの信号を入力したときは 0 [dBFS] と出力されてほしいので、"onesided2X" を指定して 0 Hz 以外の周波数成分を2倍します（パワーでは4倍）。

scale_to = "magnitude" と合わせれば、フルスケールの信号が入力されたとき、スペクトログラムの値が 1 となります。

おわりに

scipy signal ShortTimeFFT によるスペクトログラムの出力方法についてまとめました。

正直いって、スペクトログラムの相対的な値だけ知りたい場合は、fft_mode や scale_to は設定しなくてもよいと思います。dBFS を求めたいときにfft_mode や scale_to を設定すればよいでしょう。

■参考文献
[1] The SciPy community. “scipy.signal.stft”. SciPy v1.13.0 Manual. 2008-2024.
https://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.stft.html, (参照2024-04-23)
[2] The SciPy community. “scipy.signal.ShortTimeFFT”. SciPy v1.13.0 Manual. 2008-2024.
https://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.ShortTimeFFT.html, (参照2024-04-23)