
scipy signal ShortTimeFFT クラスを使用した短時間フーリエ変換について紹介します。
Pythonでスペクトログラムの表示(scipy signal ShortTimeFFT)で同様のクラスを紹介しましたが、短時間フーリエ変換についても書き留めたいと思います。
前回の記事と重複する箇所がいくつかありますが、ご容赦ください。
ShortTimeFFT について
scipy signal ShortTimeFFT は SciPy v1.12.0 で提供されたクラスです。
scipy signal では短時間フーリエ変換のための関数として stft や spectrogram を提供していましたが、Scipy v1.12.0 以降はレガシーとなり、今後はアップデートされないみたいです[1]。
ShortTimeFFT のメソッドに stft という短時間フーリエ変換するものがあるため[2]、それを使用していきます。
パラメータと返り値
ShortTimeFFT クラス
scipy signal ShortTimeFFT クラスのパラメータは以下です。
| パラメータ名 | データ型 | 概要 |
|---|---|---|
| win | np.ndarray | 分析窓関数 |
| hop | int | ホップサイズ |
| fs | float | サンプリングレート |
| fft_mode | str | スペクトログラムの出力方法(‘twosided’, ‘centered’, ‘onesided’, ‘onesided2X’) |
| mfft | int | FFT点数 |
| dual_win | np.ndarray | 合成窓関数 |
| scale_to | str | 窓関数の補正(‘magnitude’, ‘psd’) |
| phase_shift | int | 線形位相シフトの量 |
stft メソッド
短時間フーリエ変換を求めるメソッド ShortTimeFFT stft のパラメータは以下です。
| パラメータ名 | データ型 | 概要 |
|---|---|---|
| x | np.ndarray | 入力データ |
| p0 | int | 開始フレーム | p1 | int | 終了フレーム |
| k_offset | int | 開始サンプル | padding | str | パディング方法('zeros', 'edge', 'even', 'odd') | axis | int | 入力データの時間軸 |
istft メソッド
逆短時間フーリエ変換を求めるメソッド ShortTimeFFT istft のパラメータは以下です。
| パラメータ名 | データ型 | 概要 |
|---|---|---|
| x | np.ndarray | 入力データ | k0 | int | 開始サンプル |
| k1 | int | 終了サンプル | f_axis | int | 入力データの周波数軸 | t_axis | int | 入力データの時間軸 |
主な使用例
以下の操作手順を行う ShortTimeFFT の使用例を説明します。
- 短時間フーリエ変換
- 周波数成分の操作
- 逆短時間フーリエ変換
- スペクトログラム出力
ソースコード
上記の操作手順を行うソースコードは以下です。モノラルとステレオのどちらにも対応しています。ステレオの場合、スペクトログラムは L チャンネルだけグラフ出力します。
import numpy as np
import soundfile as sf
import scipy.signal as sg
import matplotlib.pyplot as plt
# WAV を読み込む
x, fs = sf.read('input.wav', always_2d=True)
x = x.T # 転置
length_x = x.shape[1] # xのデータ長
N_fft = 512 # FFT点数
# 窓関数作成
win = sg.windows.hann(N_fft) # ハン窓作成
# 短時間フーリエ変換
SFT = sg.ShortTimeFFT(win, hop=N_fft//2, fs=fs)
X_stft = SFT.stft(x)
Y_stft = np.zeros(X_stft.shape, dtype=np.complex128)
Y_stft = X_stft
# 周波数成分の操作(高域をカット)
Y_stft[:,N_fft//4:N_fft//2+1,:] = 0
# 逆短時間フーリエ変換
y = SFT.istft(Y_stft, k1=length_x)
# 対数変換
X_pow = SFT.spectrogram(x)
Y_pow = SFT.spectrogram(y)
X_dB = 10 * np.log10(np.fmax(X_pow, 1e-8))
Y_dB = 10 * np.log10(np.fmax(Y_pow, 1e-8))
# 時間軸と周波数軸の作成
N_t = np.arange(X_stft.shape[2])
t = SFT.delta_t * N_t
f = SFT.f
# グラフ作成
fig = plt.figure(figsize=(12,8))
ax1 = fig.add_subplot(2, 1, 1)
ax2 = fig.add_subplot(2, 1, 2)
vmax=np.max(X_dB[0,:,:])
vmin=np.min(Y_dB[0,:,:])
ax1.pcolormesh(t, f, X_dB[0,:,:], cmap="jet", \
vmax=vmax, vmin=vmin)
ax2.pcolormesh(t, f, Y_dB[0,:,:], cmap="jet", \
vmax=vmax, vmin=vmin)
ax1.set_ylabel('Frequency [Hz]')
ax2.set_ylabel('Frequency [Hz]')
plt.xlabel('Time [sec]')
plt.savefig("stft.png")
# 出力信号をWAVに書き込む
y = y.T # 転置
sf.write("output.wav", y, fs, subtype='PCM_16')
ソースコード説明
■ 短時間フーリエ変換(16~17行目)
基本的には ShortTimeFFT に窓関数(win)、ホップサイズ(hop)、サンプリングレート(fs)を与えてインスタンス SFT を作成して、SFT.stft に入力データを与えるだけで短時間フーリエ変換ができます。
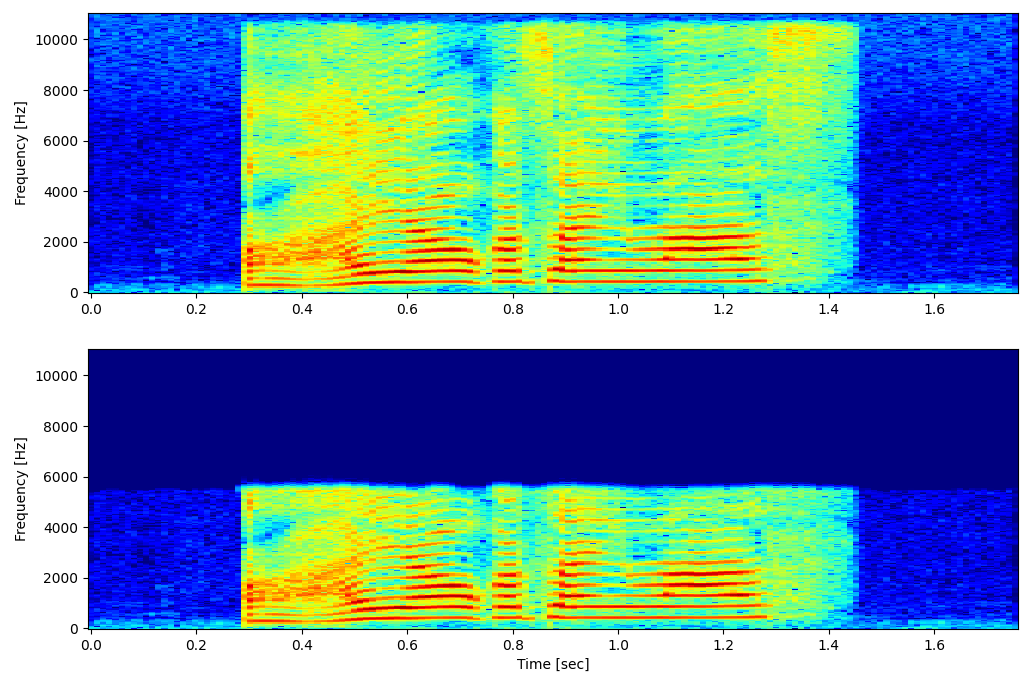
■ 周波数成分の操作(21~22行目)
簡単な周波数成分の操作としてナイキスト周波数の半分より上をカットしています。他の操作をしたい場合は、この箇所の記述を変更してください。
■ 逆短時間フーリエ変換(24~25行目)
SFT.istft に短時間フーリエ変換のデータを入れるだけで逆短時間フーリエ変換ができます。ただし、入力データ x と出力データ y の長さが異なってしまうので、k1=(xの長さ)とすることで、データ長をそろえています。
■ スペクトログラム出力(27~51行目)
SFT.spectrogram を使用してスペクトログラムを出力します。
■ WAV出力(53~55行目)
WAVファイルを出力します。sf.read と sf.write は (時間、チャンネル) という配列に対応していますが、ShortTimeFFT.stft が対応する配列は (チャンネル、時間) のため、8行目と54行目で転置しています。
出力結果
作成されたスペクトログラムを以下に示します。
ShortTimeFFT のパラメータ詳細
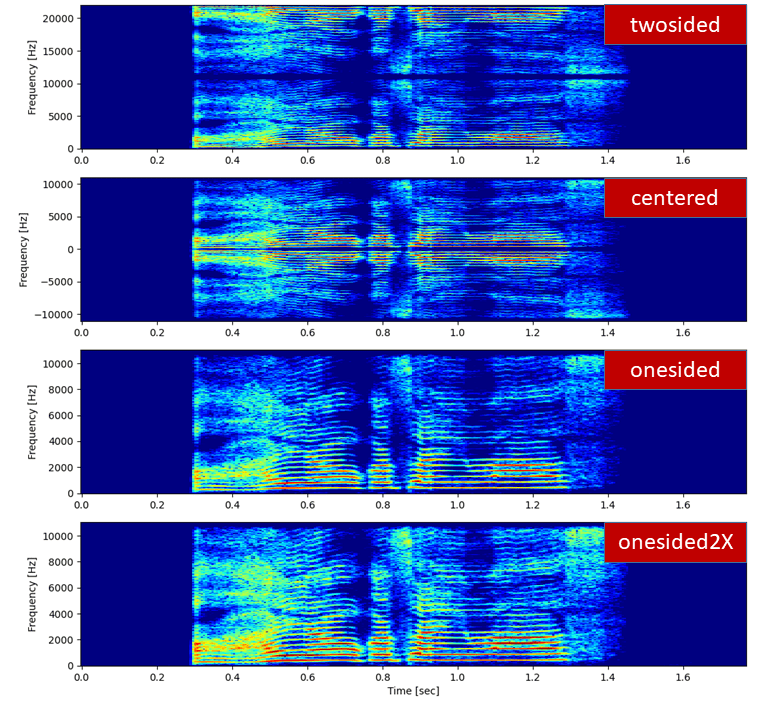
fft_mode
fft_mode には "twosided", "centered", "onesided", "onesided2X" があり、出力されるFFTの結果が変わります。以下の fs はサンプリング周波数です。
● twosided
0 [Hz] ~ fs [Hz]の短時間フーリエ変換データを出力するモード。
● centered
-fs/2 [Hz] ~ fs/2 [Hz]の短時間フーリエ変換データを出力するモード。
● onesided
0 [Hz] ~ fs/2 [Hz]の短時間フーリエ変換データを出力するモード。
● onesided2X
0 [Hz] ~ fs/2 [Hz]の短時間フーリエ変換データを出力するモード。また、0 以外の周波数成分の大きさがscale_to = "magnitude"のときは2倍、scale_to = "psd"のときは \(\sqrt{2}\) 倍 になる。
fft_modeを各モードに設定したときのスペクトログラムを以下に示します。
scale_to
scale_to には "magnitude", "psd" があります。
● magnitude
以下の補正した窓関数 \(w'\) を使用して短時間フーリエ変換を計算する。\(N\) は窓関数の大きさです。
$$
w'[n] = \frac{w[n]}{\sum_{n=0}^{N-1}w[n]}
$$
● psd
以下の補正した窓関数 \(w'\) を使用して短時間フーリエ変換を計算する。\(f_{s}\) はサンプリング周波数です。
$$
w'[n] = \frac{w[n]}{\sqrt{f_{s}\sum_{n=0}^{N-1}|w[n]|^2}}
$$
上記の補正した窓関数を使用することで、短時間フーリエ変換の絶対値の2乗を計算するだけで、パワースペクトル密度(PSD)が求められる。
phase_shift
以下のように短時間フーリエ変換後のデータ \(X[i,k]\) に対して位相シフトを行います。\(N_{shift}\) は phase_shift で指定した値です。
$$
X'[i,k] = X[i,k] \exp{\left(j 2\pi \frac{k}{N} N_{shift}\right)}
$$
おわりに
scipy signal ShortTimeFFT による短時間フーリエ変換についてまとめました。
Python で短時間フーリエ変換を使うときに参考にしてください。
■参考文献
[1] The SciPy community. “scipy.signal.stft”. SciPy v1.15.0 Manual. 2008-2024.
https://docs.scipy.org/doc/scipy-1.15.0/reference/generated/scipy.signal.stft.html, (参照2025-01-11)
[2] The SciPy community. “scipy.signal.ShortTimeFFT”. SciPy v1.15.0 Manual. 2008-2024.
https://docs.scipy.org/doc/scipy-1.15.0/reference/generated/scipy.signal.ShortTimeFFT.html, (参照2025-01-11)
