
Python でたたみ込み演算をするには scipy.signal.convolve 関数を使います。たたみ込み演算についてはフィルタをかけるときに主に使われます。
ちなみにたたみ込み演算というのは以下のような計算です(1次元)。
$$
(h*x)[n] = \sum_{m=0}^{M-1} h[m] x[n-m]
$$
Mは h の要素数です。
パラメータと返り値
scipy.signal.convolve のパラメータと返り値は以下です。
| パラメータ名 | データ型 | 概要 |
|---|---|---|
| in1 | array_like | 入力データ1 |
| in2 | array_like | 入力データ2 |
| mode | str | 出力サイズ |
| method | str | たたみ込みを計算する方法 |
| 返り値 | データ型 | 概要 |
|---|---|---|
| convolve | array | たたみ込み計算結果 |
主な使用例
1次元のデータ
1次元のデータをたたみ込むソースコードは以下です。
import numpy as np
import scipy.signal as sg
import matplotlib.pyplot as plt
# データ作成
in1 = [ 1.0 if i % 100 == 50 else 0.0 for i in range(500) ]
in2 = sg.windows.hann(50)
out = sg.convolve(in1, in2) # たたみ込む
xmax = len(out)
#figオブジェクトを作成
fig = plt.figure(figsize = (10,6))
#グラフを描画するsubplot領域を作成
ax1 = fig.add_subplot(3, 1, 1)
ax2 = fig.add_subplot(3, 1, 2)
ax3 = fig.add_subplot(3, 1, 3)
# x軸の範囲を設定
ax1.set_xlim(0, xmax)
ax2.set_xlim(0, xmax)
ax3.set_xlim(0, xmax)
#各subplot領域にデータを渡す
ax1.plot(in1)
ax2.plot(in2)
ax3.plot(out)
plt.savefig("graph.png") # グラフ保存
基本的には in1 と in2 を与えるだけでたたみ込み計算結果を返します。
保存されたグラフは以下のようになります。
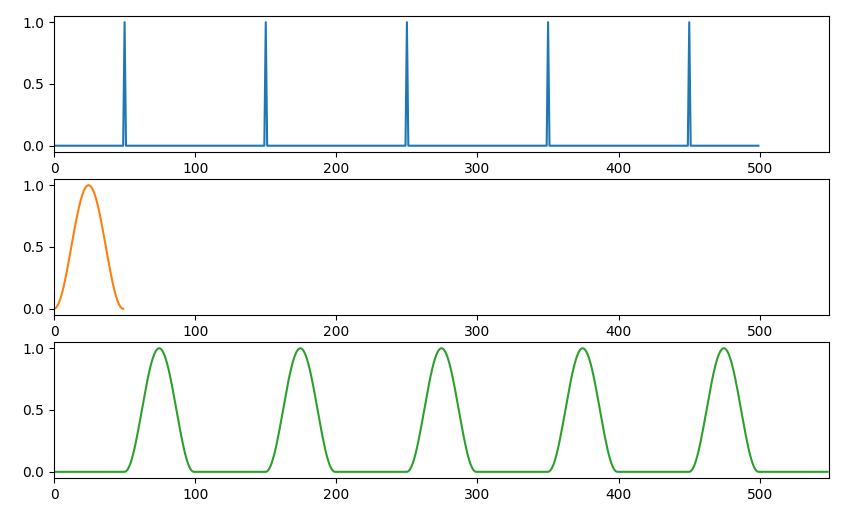
2次元のデータ
私はあまり使わないですが、2次元データのたたみ込みは以下のようになります。
import numpy as np
import scipy.signal as sg
# データ作成
in1 = [[ 1, 0, 0 ],[ 0, 1, 0 ],[ 0, 0, 1 ]]
in2 = [[ 1, 1 ],[ 1, 1 ]]
out = sg.convolve(in1, in2) # たたみ込む
print(out)
#[[1 1 0 0]
# [1 2 1 0]
# [0 1 2 1]
# [0 0 1 1]]
使用例では2次元データまでしか例を示していないですが、scipy.signal.convolveでは2次元以上のデータについてもたたみ込み可能となっています。
modeについて
各modeでのたたみ込み結果は以下のようになります。
import numpy as np
import scipy.signal as sg
# データ作成
in1 = [1, 1, 1, 1, 1, 1, 1]
in2 = [1, 1, 1, 1, 1]
out = sg.convolve(in1, in2, mode="full") # たたみ込む
print(out)
# [1 2 3 4 5 5 5 4 3 2 1]
out = sg.convolve(in1, in2, mode="valid") # たたみ込む
print(out)
# [5 5 5]
out = sg.convolve(in1, in2, mode="same") # たたみ込む
print(out)
# [3 4 5 5 5 4 3]
● full
in1(x[n])をゼロ埋めして、値を以下のように出力します。
$$
y[n] = \sum_{m=0}^{M-1} h[m] x[n-m] \hspace{1em} (n=0,...,N+M-2)
$$
● valid
ゼロ埋めを行わない要素のみ出力するモードです。
$$
y[n] = \sum_{m=0}^{M-1} h[m] x[n+(M-1)-m] \hspace{1em} (n=0,...,N-M)
$$
● same
in1 と同じ要素数の出力を返すモードです。値は full モードの中心のものとなります。
$$
y[n] = \sum_{m=0}^{M-1} h[m] x[n+((M-1)/2)-m] \hspace{1em} (n=0,...,N-1)
$$
個人的には入力と出力は同じ要素数になってほしいですが、sameにすると入力と出力の音の出だしがそろわないので困ります。そのため、full を使用して、終端の要素を削って出力を入力と同じ要素数にするかなと思います。
methodについて
method には auto、direct、fft があります。
direct と fft
● direct
direct では以下の計算式を直接計算します。
$$
(h * x)[n] = \sum_{m=0}^{M-1} h[m] x[n-m]
$$
● fft
fft では以下のようにFFTを使用してたたみ込みを計算します。
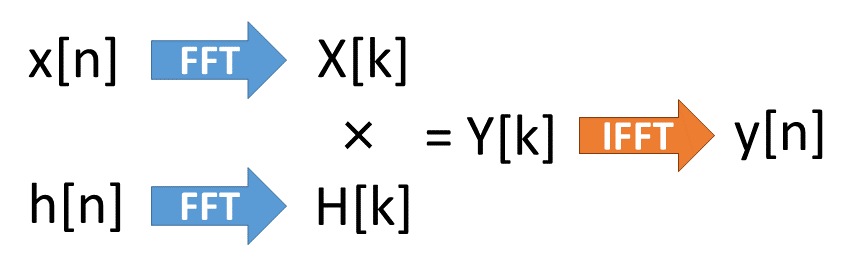
一見回りくどいことをしているようですが、FFTという高速計算によってNが大きければ大きいほど計算時間が direct よりも小さくなります。
● auto
auto では in1 と in2 のデータサイズによって計算速度が速い方を direct か fft で選択します 。
計算速度
私の環境の各 method の計算速度を以下に示します。M=Nとしています。
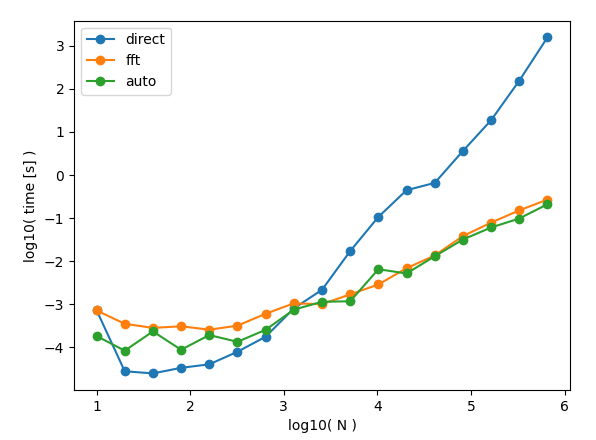
direct の場合、N=10^6 では計算時間が1000秒くらいですが、fft は1秒以内に計算が終わっています。こんな感じでデータ数が大きいときの FFT の効果がわかると思います。
ただ、N=1000 以下では direct のほうが計算が速いです。
そのため、データサイズによって計算方法を変える auto が一番良いかと思います。
おわりに
本記事では、たたみ込みを計算する関数 scipy.signal.convolve について紹介しました。私もscipy.signal.convolve を使うとき、mode をどのように設定すればよいか迷うので、この記事が同じような人の助けになれば幸いです。
■参考文献
[1] The SciPy community. “scipy.signal.convolve”. SciPy v1.12.0 Manual. 2008-2024.
https://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.convolve.html, (参照2024-03-27)
■変更履歴
・2025/02/23:「3.modeについて」のfullの計算式でh[k]となっていたため、h[m]に修正
