前回の記事(MP3のフィルタバンクについて)でMP3のフィルタバンクを導出しましたので、今回はMP3のフィルタバンクの効率的な計算方法について紹介します。
MP3のフィルタバンクについて
前回の記事(MP3のフィルタバンクについて)でも説明しましたが、あらためてMP3のフィルタバンクについて説明したいと思います。
MP3のフィルタバンク(コサイン変調フィルタバンク)のブロック図は以下です。\(M\ \)はフィルタバンクの数となります。
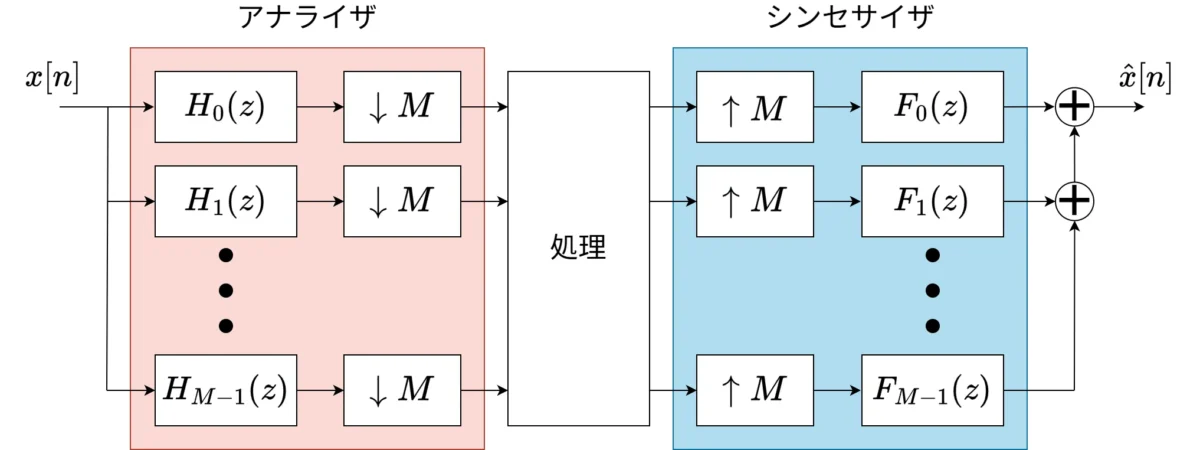
↓M はデシメータ、↑M はインタポレータです。
\(H_{k}(z)\), \(F_{k}(z)\ \)のフィルタ係数\(\ h_{k}\), \(f_{k}\ \)については以下のように表されます。
\begin{align}
h_{k}[n] &= 2\ p_{0}[n]\cos{\left(\frac{\pi}{M}\left(k+\frac{1}{2}\right)\left(n-\frac{N}{2}\right)+\theta_{k}\right)} \tag{1}\\[5pt] f_{k}[n] &= 2\ p_{0}[n]\cos{\left(\frac{\pi}{M}\left(k+\frac{1}{2}\right)\left(n-\frac{N}{2}\right)-\theta_{k}\right)} \tag{2}
\end{align}
$$
ここで、\(N\ \)はフィルタの次数、\(\theta_{k}=(-1)^{k}(\pi/4)\ \)、\(p_{0}[n]\ \)はプロトタイプフィルタ\(\ P_{0}(z)\ \)のフィルタ係数です。
MP3のフィルタバンクでは、「処理」ブロックで何もしないときでも、復元信号\(\ \hat{x}[n]\ \)は完全に元の信号には戻りませんが、ある程度元の信号に戻ります。
効果的構成
上記の(1)式と(2)式でフィルタバンクを計算してもよいですが、アナライザの出力を計算するだけでも、N+1点のフィルタをM回畳み込む必要があるため、かなりの計算量を必要とします。そのため、計算量を減らす効率的な方法を紹介します。
文献[1][2]を参考にしていますが、筆者独自の記述が含まれているので、間違いがある可能性をご承知おきください。
アナライザ
まず、アナライザではプロトタイプフィルタ\(\ P_{0}(z)\ \)を次式のように2M個のポリフェーズフィルタに分解します。
\begin{align}
P_{0}(z) &= \sum_{i=0}^{2M-1} G_{i}(z^{2M}) z^{-i} \tag{3} \\[5pt] G_{i}(z) &= \sum_{l=0}^{L-1} p_{0}[2Ml+i]z^{-l} \tag{4}
\end{align}
$$
ここで、\(L=(N+1)/2M\ \)となります。
\(\ H_{k}(z)\ \)の途中式(前回の記事(MP3フィルタバンクについて)の(33)式)に(3)式を代入することで、\(G_{i}(z^{2M}\cdot e^{-j2\pi(k+1/2)})=G_{i}(-z^{2M})\ \)より、
\begin{align}
&\ H_{k}(z) \\[5pt] &=\ a_{k}U_{k}(z)+a_{k}^{*}V_{k}(z) \\[5pt] &=\ e^{j\theta_{k}} e^{-jN\frac{\pi}{M}(k+1/2)/2} P_{0}(z\cdot e^{-j\frac{\pi}{M}(k+1/2)}) \\[2pt] &\hspace{1em} + e^{-j\theta_{k}} e^{jN\frac{\pi}{M}(k+1/2)/2} P_{0}(z\cdot e^{j\frac{\pi}{M}(k+1/2)}) \\[5pt] &=\ e^{j\theta_{k}} e^{-jN\frac{\pi}{M}(k+1/2)/2} \sum_{i=0}^{2M-1} e^{j\frac{\pi}{M}(k+1/2)i} G_{i}(-z^{2M})z^{-i} \\
&\hspace{1em} + e^{-j\theta_{k}} e^{jN\frac{\pi}{M}(k+1/2)/2} \sum_{i=0}^{2M-1} e^{-j\frac{\pi}{M}(k+1/2)i} G_{i}(-z^{2M})z^{-i} \\[5pt] &=\ \sum_{i=0}^{2M-1} 2\cos{\left(\frac{\pi}{M}\left(k+\frac{1}{2}\right)\left(i-\frac{N}{2}\right)+\theta_{k}\right)} G_{i}(-z^{2M})z^{-i} \\[5pt] &=\hspace{1em} \sum_{i=0}^{2M-1} c_{ki} G_{i}(-z^{2M})z^{-i} \tag{5}
\end{align}
$$
となります。\(c_{ki}\ \)は以下のように置き換えたものです。
c_{ki} = 2\cos{\left(\frac{\pi}{M}\left(k+\frac{1}{2}\right)\left(i-\frac{N}{2}\right)+\theta_{k}\right)} \tag{6}
$$
ここで、\(G_{i}(-z^{2M})\ \)は以下のように表されます。
G_{i}(-z^{2M}) = \sum_{l=0}^{L-1} (-1)^{l} p_{0}[2Ml+i]z^{-2Ml} \tag{7}
$$
(5)式より各フィルタバンクの出力\(\ y_{k}[m]\ \)は以下のようになります。
\begin{align}
y_{k}[m] &= \sum_{i=0}^{2M-1} c_{ki} z_{i}[m] \tag{8} \\[5pt] z_{i}[m] &= \sum_{l=0}^{L-1} (-1)^{l}p_{0}[2Ml+i]x[2Mm-(2Ml+i)] \tag{9}
\end{align}
$$
(8)式と(9)式はわかりにくいですが、ブロック図にすると以下のようになり、わかりやすくなるかと思います。
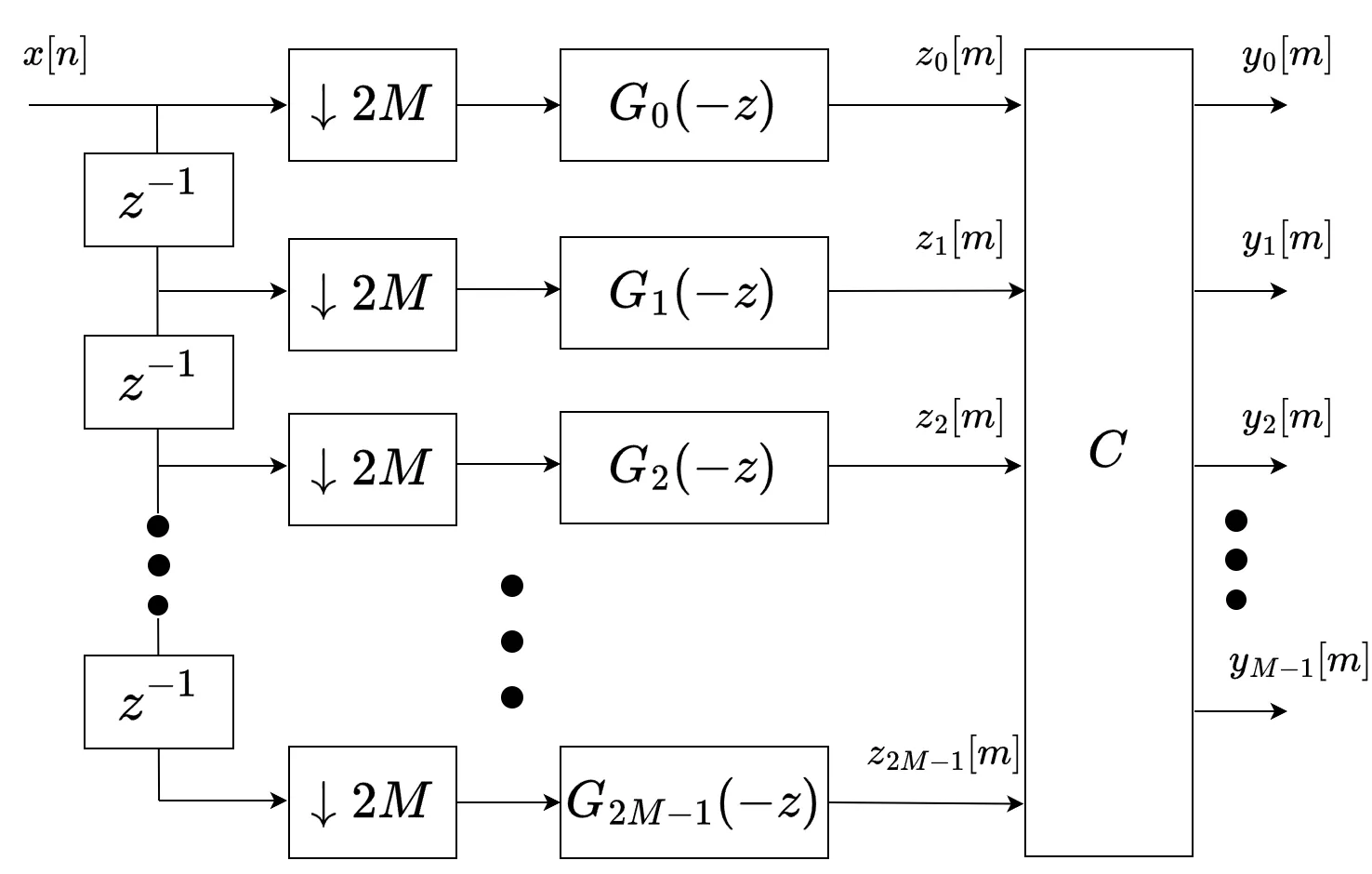
各遅延器で遅延させた後、1/2Mにデシメーションさせ、\(G_{i}(-z)\ \)フィルタを畳み込み、\(\ z_{i}[m]\ \)を作成します。その後、以下の式によって\(\ y_{k}[m]\ \)が求まります。
\begin{bmatrix}
y_{0}[m] \\
\vdots \\
y_{k}[m] \\
\vdots \\
y_{M-1}[m] \end{bmatrix}=
{\boldsymbol C}
\begin{bmatrix}
z_{0}[m] \\
\vdots \\
z_{i}[m] \\
\vdots \\
z_{2M-1}[m] \end{bmatrix} \tag{10}
$$
{\boldsymbol C}
=
\begin{bmatrix}
c_{00} & \cdots & c_{0i} & \cdots & c_{0,2M-1} \\
\vdots & \ddots & \vdots & & \vdots \\
c_{k0} & \cdots & c_{ki} & \cdots & c_{k,2M-1} \\
\vdots & & \vdots & \ddots & \vdots \\
c_{M-1,0} & \cdots & c_{M-1,i} & \cdots & c_{M-1,2M-1} \\
\end{bmatrix} \tag{11}
$$
\(C\ \)はM x 2M の行列です。
\(G_{i}(-z)\ \)フィルタの畳み込みについては、\(G_{i}(z)\ \)の奇数番目のフィルタ係数の符号を逆にして、フィルタを畳み込めばよいです。
上記のように計算することで、N+1点の畳み込みをM回行わなければならなかったところ、
(N+1)/2M点の畳み込みを2M回行うだけで済みます。
シンセサイザ
シンセサイザにおけるフィルタ\(\ F_{k}(z)\ \)ついては\(\ H_{k}(z)\ \)との関係式(前回の記事(MP3フィルタバンクについての(17)式)と(5)式より、
\begin{align}
&F_{k}(z) \\[5pt] &= z^{-N} H_{k}(z^{-1}) \\[5pt] &= z^{-N}\sum_{i=0}^{2M-1} c_{ki} G_{i}(-z^{-2M})z^{i} \\[5pt] &= \sum_{i=0}^{2M-1} c_{ki} z^{-N}G_{i}(-z^{-2M})z^{i} \\[5pt] &= \sum_{i=0}^{M-1} z^{i} (c_{ki} z^{-(2ML-1)}G_{i}(-z^{-2M}) + \sum_{i=0}^{M-1}c_{k,M+i} z^{-(2ML-1)}G_{M+i}(-z^{-2M})z^{M}) \\[5pt] &= \sum_{i=0}^{M-1} z^{-M+i+1} (c_{ki} z^{-M(2L-1)}G_{i}(-z^{-2M}) + \sum_{i=0}^{M-1}c_{k,M+i} z^{-M(2L-2)}G_{M+i}(-z^{-2M})) \tag{12}\\[5pt] \end{align}
$$
となります。
上式から\(\ 0\leq i\leq M-1\ \)において復元信号 \(\ \hat{x}[n]\ \)は以下のようになり、筆者本人ですら見るのが嫌になるくらい長い式となります。
\begin{align}
&\hat{x}[Mm+M-1-i] \\[5pt] =&\ \sum_{k=0}^{M-1}c_{ki}\sum_{l=0}^{L-1}(-1)^{l}p_{0}[2Ml+i]y_{k}[m+2l-(2L-1)] \\[5pt] &+\ \sum_{k=0}^{M-1}c_{k,M+i}\sum_{l=0}^{L-1}(-1)^{l}p_{0}[2Ml+M+i]y_{k}[m+2l-(2L-2)] \\[5pt] =&\ \sum_{l=0}^{L-1}(-1)^{l}p_{0}[2Ml+i]\sum_{k=0}^{M-1}c_{ki}y_{k}[m+2l-(2L-1)] \\[5pt] &+\ \sum_{l=0}^{L-1}(-1)^{l}p_{0}[2Ml+M+i]\sum_{k=0}^{M-1}c_{k,M+i}y_{k}[m+2l-(2L-2)] \\[5pt] =&\ \sum_{l=0}^{L-1}(-1)^{l}p_{0}[2Ml+i] v_{i}[m+2l-(2L-1)] \\[5pt] &+\ \sum_{l=0}^{L-1}(-1)^{l}p_{0}[2Ml+M+i] v_{M+i}[m+2l-(2L-2)] \tag{13}
\end{align}
$$
上式はとてもわかりにくいですが、復元信号 \(\ \hat{x}[n]\ \)を求めるまでのブロック図(下図)を見ると少しわかりやすくなるかと思います。
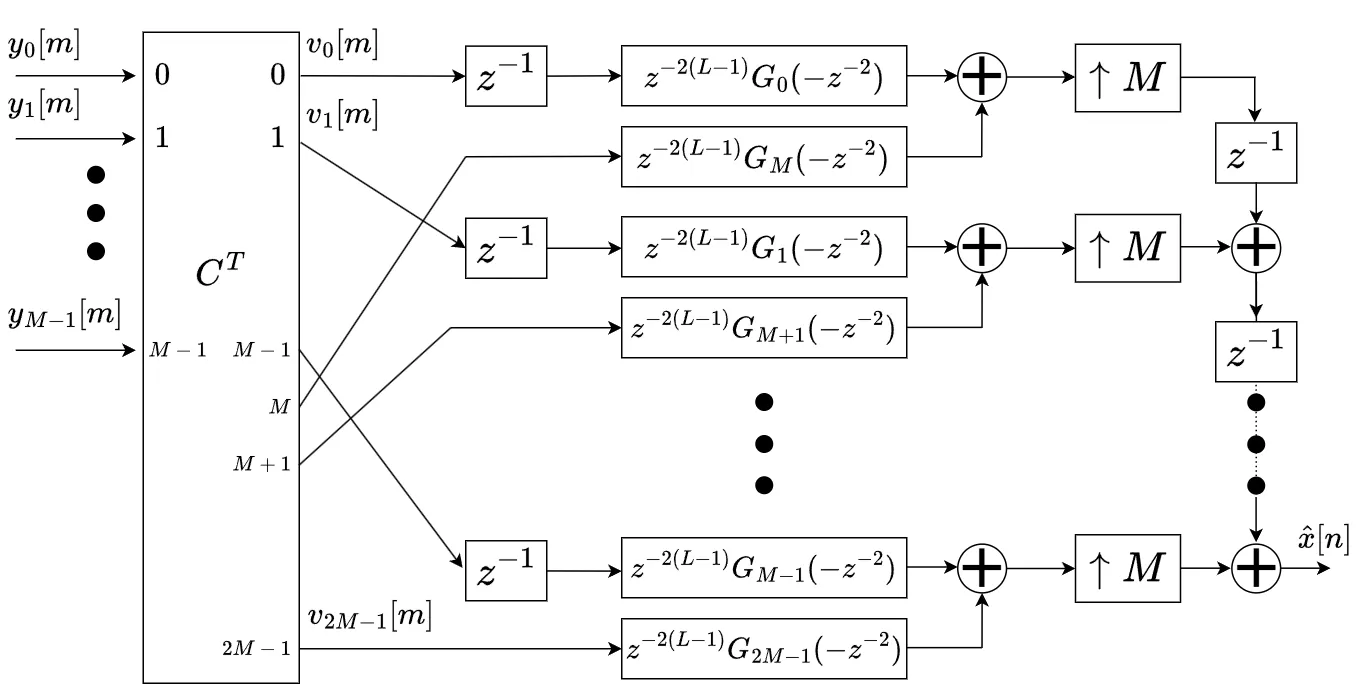
まず、以下の式によって\(\ v_{i}[m]\ \)を求めます。
\begin{bmatrix}
v_{0}[m] \\
\vdots \\
v_{i}[m] \\
\vdots \\
v_{2M-1}[m] \end{bmatrix}=
{\boldsymbol C^T}
\begin{bmatrix}
y_{0}[m] \\
\vdots \\
y_{k}[m] \\
\vdots \\
y_{M-1}[m] \end{bmatrix} \tag{14}
$$
次に\(\ v_{i}\ (i=0,\cdots,M-1)\ \)に対して\(\ z^{-2(L-1)-1}G_{i}(-z^{-2})\ \)のフィルタを畳み込みます。\(\ v_{M+i}\ \) に対しては\(\ z^{-2(L-1)}G_{M+i}(-z^{-2})\ \)の畳み込みを計算します。
\(i=1\),\(\ N+1=24\),\(\ M=3\),\(\ L=4\ \)のとき、\(\ z^{-2(L-1)-1}G_{1}(-z^{-2})\ \)のフィルタ係数は以下のように段階を踏んで求めることができます。
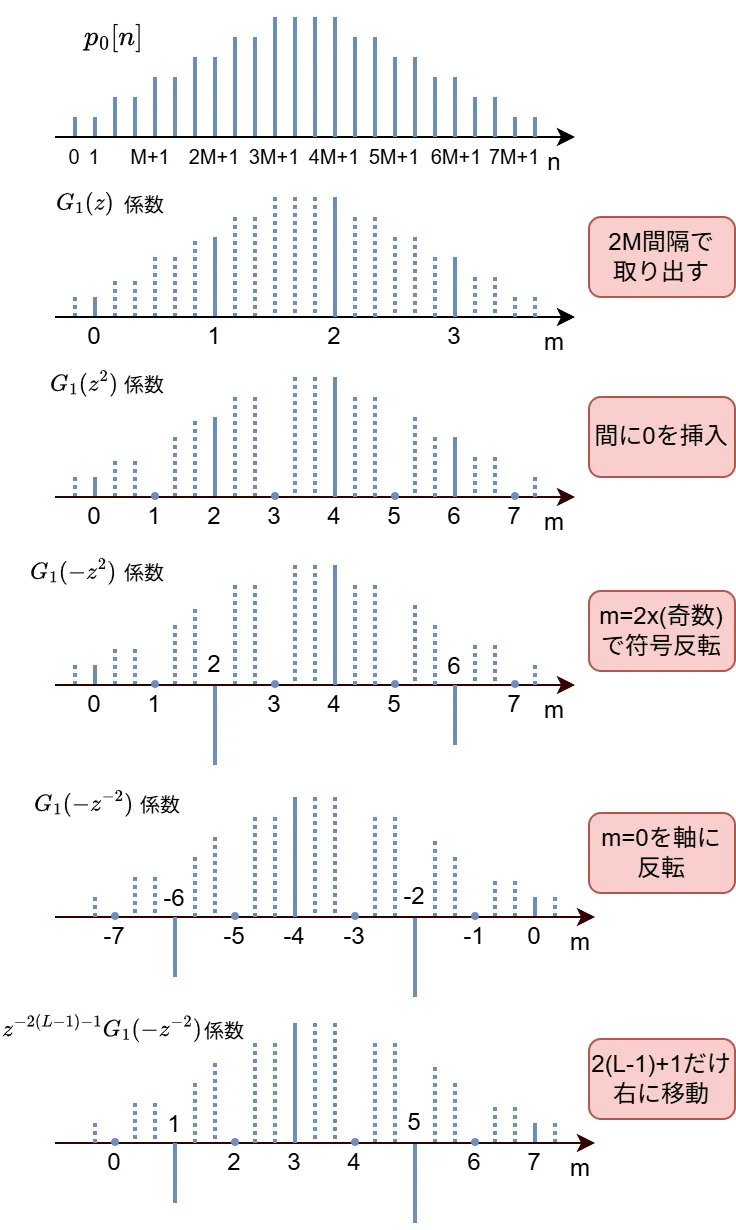
つまり、\(G_{i}(-z^{2})\ \)のフィルタ係数を逆順にしたものが\(\ z^{-2(L-1)-1}G_{i}(-z^{-2})\ \)のフィルタ係数となります。
\(M+i\ \)に対しては最後に右に移動させる点数は\(\ 2(L-1)\ \)点となります。\(\ z^{-2(L-1)}G_{4}(-z^{-2})\ \)のフィルタ係数は以下です。
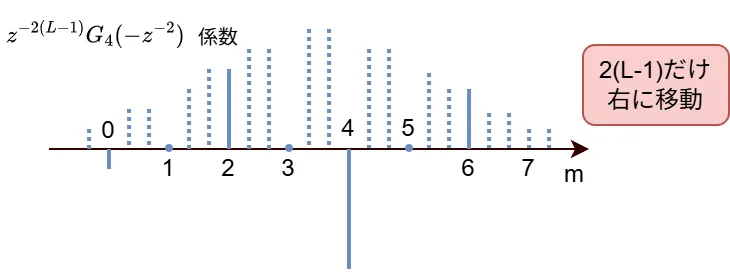
上記手順で求めたフィルタを\(\ v_{i}, v_{M+i}\ \)にそれぞれ畳み込み、足し合わせ、Mにインタポレーションしたものが\(\ \hat{x}[Mm+M-1-i]\ \)の値となります。
おわりに
本記事では、MP3のフィルタバンクを計算する効率的な方法について紹介しました。計算式が大量にあって、見づらいかもしれませんが、参考書には計算式や説明がなく、筆者が理解するのに時間がかかったため、あえて途中式も多めに記載しています。もし、計算式に間違いなどございましたらご指摘ください。
次回はPythonでMP3のフィルタバンクを実装してみたいと思います。
■参考文献
[1] 貴家仁志, 「マルチレート信号処理 ディジタル信号処理シリーズ 第14巻」, 株式会社昭晃堂, 1995.
[2] Jayaraman J. Thiafarajan, "Analysis of the MPEG-1 LayerⅢ (MP3) Algorithm Using MATLAB," Morgan & Claypool Publishers, 2011.
■変更履歴
・2025/06/30:タイトルを変更
