MP3のフィルタバンクを実装

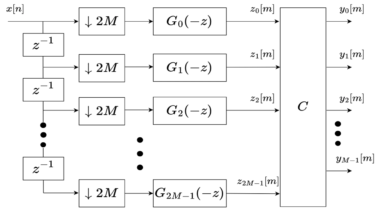
本記事では、MP3の規格書[1]に則ってMP3のフィルタバンクを実装しました。前回の記事（MP3のフィルタバンクを効率的に計算）の続きです。

実装手順について説明したのち、その詳細について解説したいと思います。それから、手順通りにプログラムを書いて、動作を確認します。

1 MP3における実装手順
- 1.1 アナライザ
- 1.2 シンセサイザ
2 実装の解説
- 2.1 アナライザの計算
- 2.2 シンセサイザの計算
3 プログラム
- 3.1 ソースコード
- 3.2 実行方法
4 動作確認
5 おわりに

MP3における実装手順

MP3の実装手順を説明します。MP3では、フィルタの次数 $N=511$、フィルタバンクの数$\ M=32$、$\ L=(N+1)/2M=8\ $でフィルタバンクを求めていきます。

アナライザ

帯域ごとに分割した信号は以下の手順で作成できます。数式の記号はMP3の規格書に書いてある通りに記載しています。

データ取得

まず、$M=32\ $点ごとに配列 ${\mathsf X}[{\mathsf i}]$にデータを以下のように格納していきます。

$$
\begin{align}
{\mathsf X}_{\mathsf i} &= {\mathsf X}_{\mathsf i-32} & ({\mathsf i}=511,\ 510,\ \cdots,32) \tag{1}\\[5pt] {\mathsf X}_{\mathsf i} &= {\rm NEXT DATA} & ({\mathsf i}=31,\ 30,\ \cdots,0) \tag{2}
\end{align}
$$

シフトによって一番古い32個のデータは捨てられ、新しい32個のデータを格納していきます。

フィルタ係数を乗算

次にフィルタ係数$\ {\mathsf C}_{\mathsf i}\ $を$\ {\mathsf X}_{\mathsf i}\ $に乗算します。

$$
{\mathsf Z}_{\mathsf i} = {\mathsf C}_{\mathsf i}{\mathsf X}_{\mathsf i} \hspace{1em} ({\mathsf i}=0,\ 1,\ \cdots,511) \tag{3}
$$

MP3では下図のフィルタ係数 $\ {\mathsf C}_{\mathsf i}\ $を使用します。

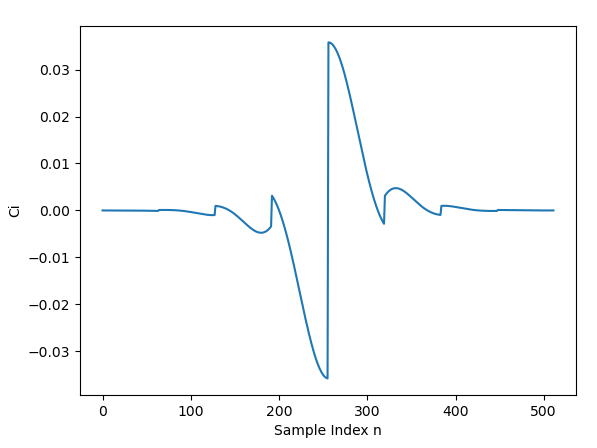
フィルタ係数 $\ {\mathsf C}_{\mathsf i}\ $のテキストデータは以下をクリックするとダウンロードできます[1]。

フィルタ係数$\ {\mathsf C}_{\mathsf i}\ $のテキストファイルをダウンロード

帯域分割信号を生成

以下の式で$\ {\mathsf Y}_{\mathsf i} $を計算します。

$$
{\mathsf Y}_{\mathsf i} = \sum_{\mathsf j=0}^{7} {\mathsf Z}_{{\mathsf i}+64 {\mathsf j}} \hspace{1em} ({\mathsf i}=0,\cdots,63) \tag{4}
$$

最後に以下の式で帯域分割信号 $\ {\mathsf S}_{\mathsf i}\ $を計算できます。

$$
{\mathsf S}_{\mathsf i} = \sum_{\mathsf k=0}^{63} {\mathsf M}_{\mathsf i \mathsf k}{\mathsf Y}_{\mathsf k} \hspace{1em} (\mathsf i=0,\cdots,31) \tag{5}
$$

ここで、${\mathsf M}_{\mathsf i \mathsf k}\ $の値は以下となります。

$$
{\mathsf M}_{\mathsf i \mathsf k} = \cos{\left(\frac{\mathsf \pi}{64}(2 \mathsf i+1)(\mathsf k-16)\right)} \tag{6}
$$

シンセサイザ

復元信号の合成方法は以下となります。

${\mathsf V}_{\mathsf i}\ $を計算

まず、1024個の配列 ${\mathsf V}_{\mathsf i}\ $を用意して、64点シフトさせます。

$$
{\mathsf V}_{\mathsf i} = {\mathsf V}_{\mathsf i-64} \hspace{1em} (\mathsf i=1023,\ 1022,\ \cdots, 64) \tag{7}
$$

シフトで空いた場所に以下の式で計算した新しいデータを詰めていきます。

$$
{\mathsf V}_{\mathsf i} = \sum_{\mathsf k=0}^{31} {\mathsf N}_{\mathsf i \mathsf k}{\mathsf S}_{\mathsf k} \hspace{1em}(\mathsf i=0,1,\cdots, 63) \tag{8}
$$

${\mathsf N}_{\mathsf i \mathsf k}\ $の値は以下となります。

$$
{\mathsf N}_{\mathsf i \mathsf k} = \cos{\left(\frac{\mathsf \pi}{64}(2 \mathsf k+1)(\mathsf i+16)\right)} \tag{9}
$$

${\mathsf V}_{\mathsf i}\ $を$\ {\mathsf U}_{\mathsf i}\ $に詰める

${\mathsf V}_{\mathsf i}\ $を${\mathsf U}_{\mathsf i}\ $に以下の式で詰めていきます。

$$
\begin{align}
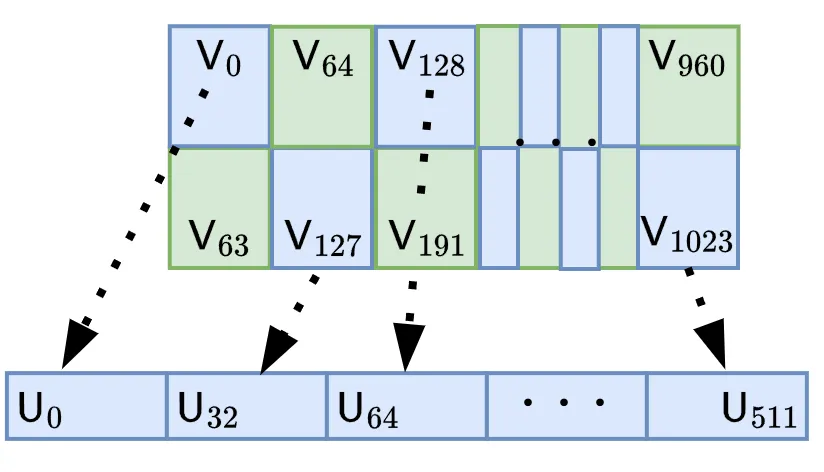
{\mathsf U}_{64\mathsf i+\mathsf j} &= {\mathsf V}_{128\mathsf i+\mathsf j} \tag{10}\\[5pt] {\mathsf U}_{64\mathsf i+32+\mathsf j} &= {\mathsf V}_{128\mathsf i+96+\mathsf j} \tag{11}\\[5pt] \end{align}
$$

図で表すと以下のような感じです。

フィルタ係数を乗算

フィルタ係数$\ {\mathsf D}_{\mathsf i} $を$\ {\mathsf U}_{\mathsf i}\ $に乗算して$\ {\mathsf W}_{\mathsf i}\ $を計算します。

$$
{\mathsf W}_{\mathsf i} = {\mathsf D}_{\mathsf i}{\mathsf U}_{\mathsf i} \hspace{1em}(\mathsf i=0,\cdots,511) \tag{12}
$$

フィルタ係数 $\ {\mathsf D}_{\mathsf i}\ $のグラフは以下となってます。アナライザで使用した$\ {\mathsf C}_{\mathsf i}\ $と比較して、形は同じですが、値の大きさが変わっている感じです。

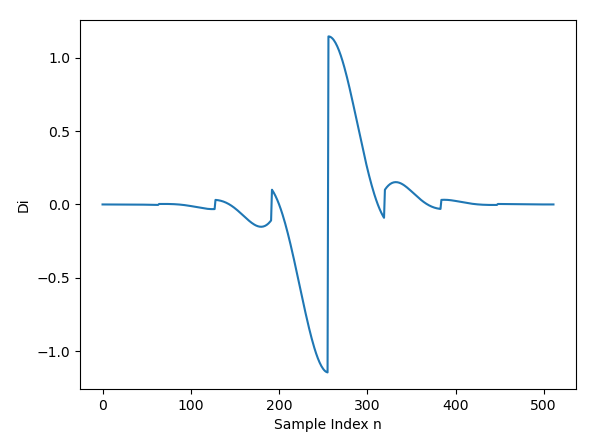
フィルタ係数 $\ {\mathsf D}_{\mathsf i}\ $のテキストデータは以下をクリックするとダウンロードできます[1]。

フィルタ係数$\ {\mathsf D}_{\mathsf i}\ $のテキストファイルをダウンロード

復元信号を合成

最後に以下の式を計算することで復元信号$\ \hat{\mathsf S}_{\mathsf j}\ $を合成することができます。

$$
\hat{\mathsf S}_{\mathsf j} = \sum_{\mathsf i=0}^{15} {\mathsf W}_{\mathsf j+32 \mathsf i} \hspace{1em}(j=0,\cdots,31) \tag{13}
$$

実装の解説

さきほど紹介したMP3のフィルタバンクの実装について、なぜこれでフィルタバンクを実装できるか説明します。結構マニアックな内容となりますので、興味がある方以外は読み飛ばしたほうがいいかもしれないです。

解説については筆者独自のものであるため間違いがある可能性をご承知おきください。

前回の記事を頻繁に参照しますので、別ページで記事を開いておくことをお勧めします。

MP3のフィルタバンクを効率的に計算

前回の記事（MP3のフィルタバンクについて）でMP3のフィルタバンクを導出しましたので、今回はMP3のフィルタバンクの効率的な計算方法について紹介します。 MP3のフィルタバンクについて前回の記事（MP3のフィルタバンクについて）でも説明[…]

アナライザの計算

前回の記事の帯域分割信号 $y_{k}\ $の求め方を以下に再掲します。

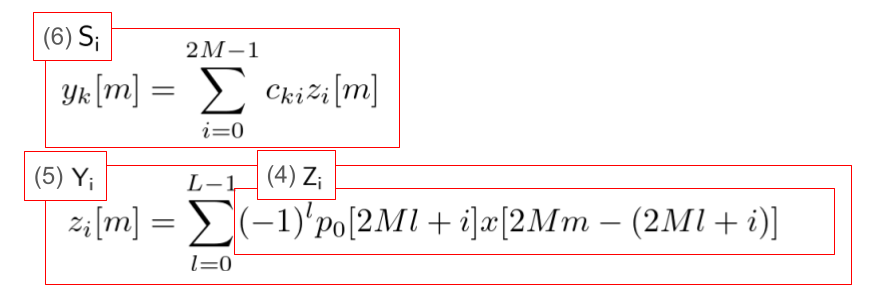
(4)～(6)式に相当する部分が赤い枠となっており、帯域分割信号を計算しています。

アナライザのブロック図も再掲します。

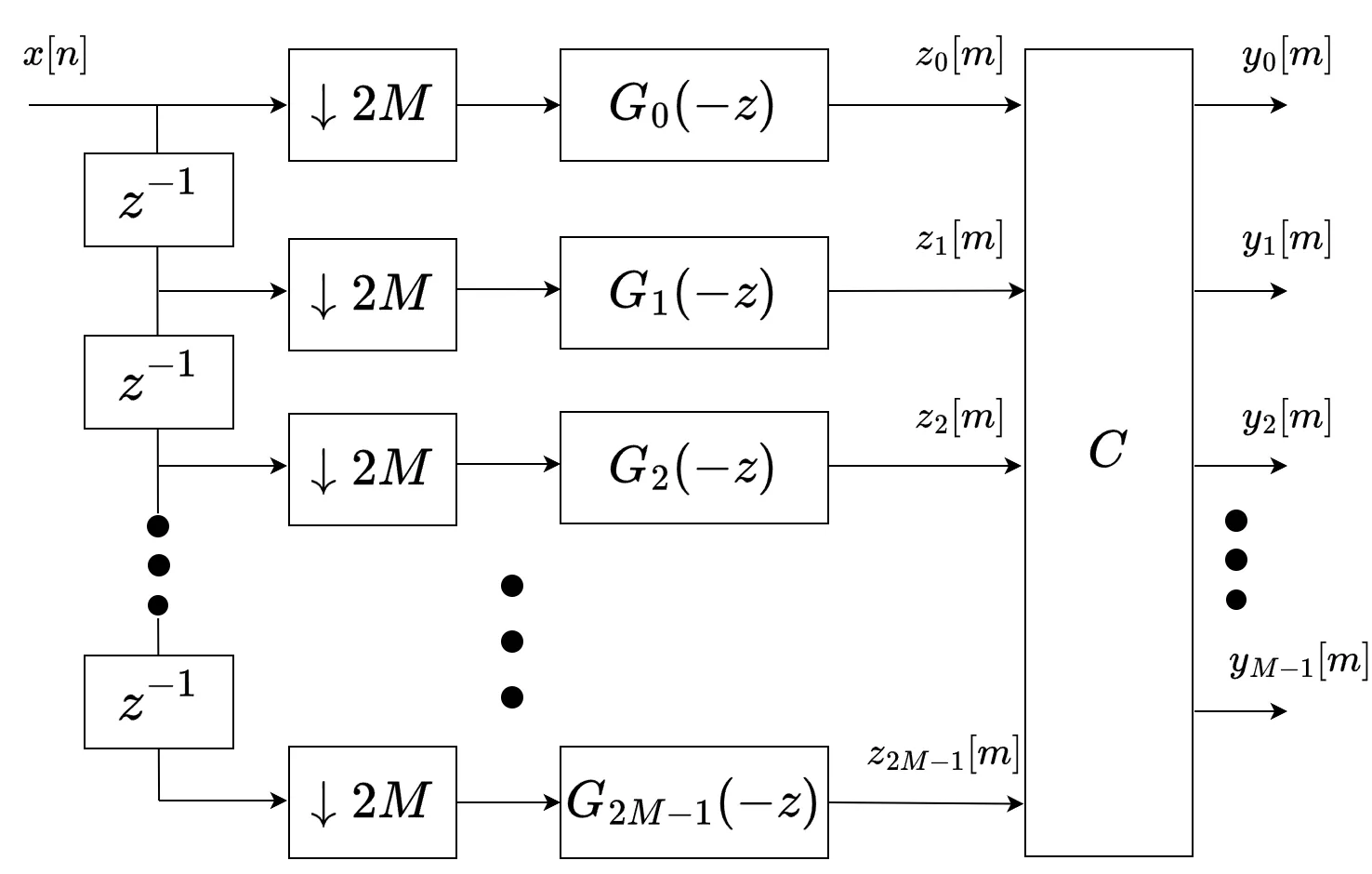
アナライザのフィルタ係数

フィルタ係数 $\ {\mathsf C}_{\mathsf i}\ $についてはプロトタイプフィルタ$\ p_{0}[n]\ $を2M 点周期で符号を反転したものとなります。

$$
{\mathsf C}_{\mathsf i} =
\left\{
\begin{array}{ll}
-p_{0}[i] & (\lfloor \frac{i}{64} \rfloor が奇数) \\[5pt] p_{0}[i] & ({\rm otherwise})
\end{array}
\right. \tag{14}
$$

(14)式であらかじめ符号反転しておくことで、(4)式の計算を簡略化しています。

MP3で使用しているプロトタイプフィルタ$\ p_{0}[n]\ $のグラフは以下となります。

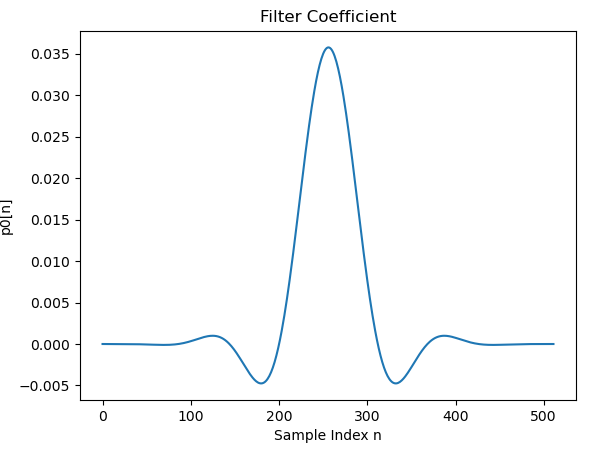
また、MP3のプロトタイプフィルタを使用した帯域分割フィルタの周波数特性は以下になります。

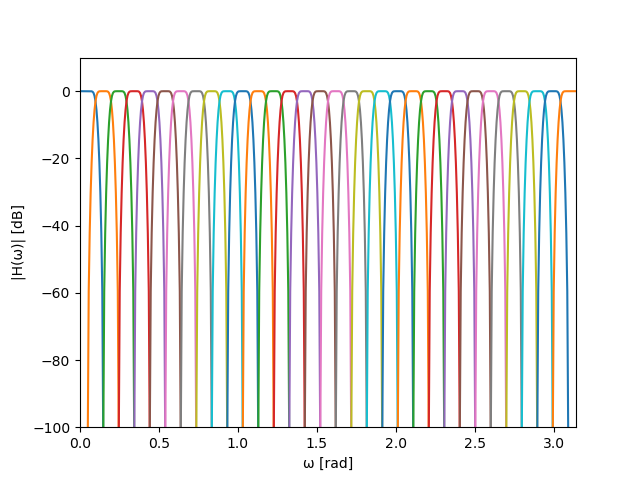
${\mathsf M}_{\mathsf i \mathsf k}\ $について

${\mathsf M}_{\mathsf i \mathsf k}\ $については前回の記事の$\ c_{ki}\ $に相当するものですが、$c_{ki}\ $の計算式は以下のように$\ {\mathsf M}_{\mathsf i \mathsf k}\ $と異なっています。

$$
c_{ki} = 2\cos{\left(\frac{\pi}{M}\left(k+\frac{1}{2}\right)\left(i-\frac{N}{2}\right)+(-1)^{k}\frac{\pi}{4}\right)} \tag{15}
$$

定数に数字を入れて表現の仕方を合わせても以下のように差異があります。

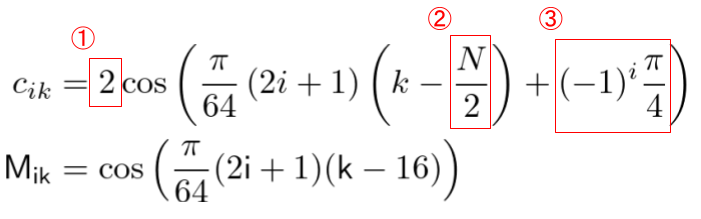
赤い枠で囲んだところが数式の差異です。この差異の箇所について順番に説明していきます。

1. 係数2について

係数２がなくなっていますが、これについてはフィルタ係数$\ {\mathsf C}_{\mathsf i}\ $に含まれています。

要は厳密にいうと、(14)式は以下のようになるということです。

$$
{\mathsf C}_{\mathsf i} =
\left\{
\begin{array}{ll}
-2p_{0}[i] & (\lfloor \frac{i}{64} \rfloor が奇数) \\[5pt] 2p_{0}[i] & ({\rm otherwise})
\end{array}
\right. \tag{14’}
$$

2. N/2の削除

N/2 についてですが、ここの値は使用するプロトタイプフィルタによって値が変わり、プロトタイプフィルタの対称軸の位置となります。

つまり、下図の位置ということです。

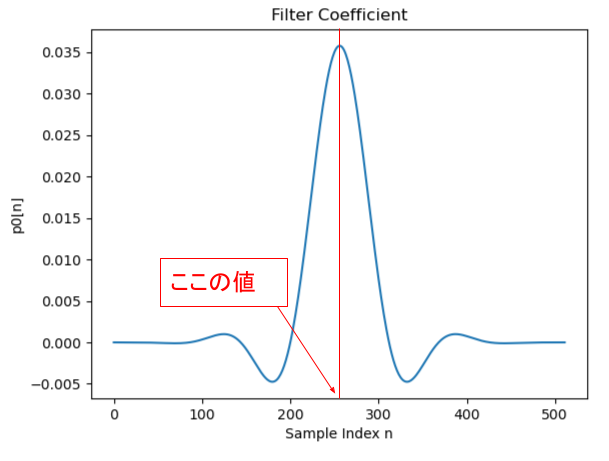
MP3で使用するプロトタイプフィルタの場合、$\ p_{0}[n+1]=p_{0}[N-n]\ $であり、対称軸の位置は $\ (N+1)/2\ $となります。

したがって、以下のように式変形されます。

$$
\begin{align}
&\cos{\left(\frac{\pi}{64}\left(2i+1\right)\left(k-\frac{N+1}{2}\right)+(-1)^{i}\frac{\pi}{4}\right)} \\[5pt] =& \cos{\left(\frac{\pi}{64}\left(2i+1\right)\left(k-256\right)+(-1)^{i}\frac{\pi}{4}\right)} \\[5pt] =& \cos{\left(\frac{\pi}{64}\left(2i+1\right)k-8\pi i -4\pi+(-1)^{i}\frac{\pi}{4}\right)} \\[5pt] =& \cos{\left(\frac{\pi}{64}\left(2i+1\right)k+(-1)^{i}\frac{\pi}{4}\right)} \tag{16}
\end{align}
$$

3. $(-1)^{i}\pi/4\ $の変更

$(-1)^{i}\pi/4\ $については$-(-1)^{i}\pi/4\ $でも良いです（参照：MP3のフィルタバンクについて $\ a_{k}\ $の決め方の補足）。

また、$-(-1)^{i}\pi/4\ $については$\ -\pi/2(i+0.5) $とも表せます。

そのため、式は以下のように変形でき、最終的に$\ {\mathsf M}_{\mathsf i \mathsf k}\ $と同じになります。

$$
\begin{align}
& \cos{\left(\frac{\pi}{64}\left(2i+1\right)k-\frac{\pi}{2}(i+\frac{1}{2})\right)} \\[5pt] =& \cos{\left(\frac{\pi}{64}\left(2i+1\right)(k-16)\right)} \tag{17}
\end{align}
$$

シンセサイザの計算

前回の記事の復元信号 $\ \hat{x}[n]\ $の求め方を以下に再掲します。

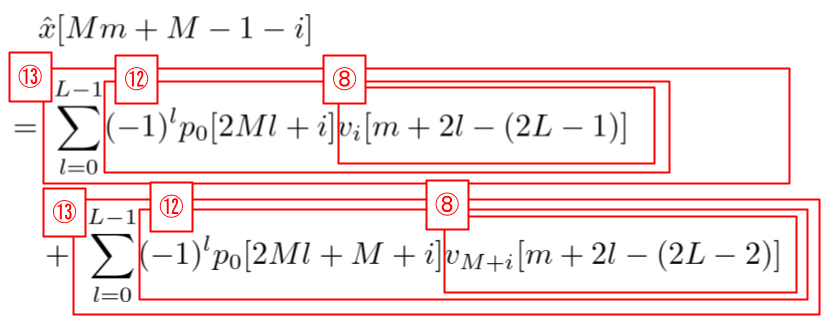
(8)式、(12)式、(13)式に相当する部分が上記の赤い枠で囲んだものとなっています。

シンセサイザのブロック図も再掲します。

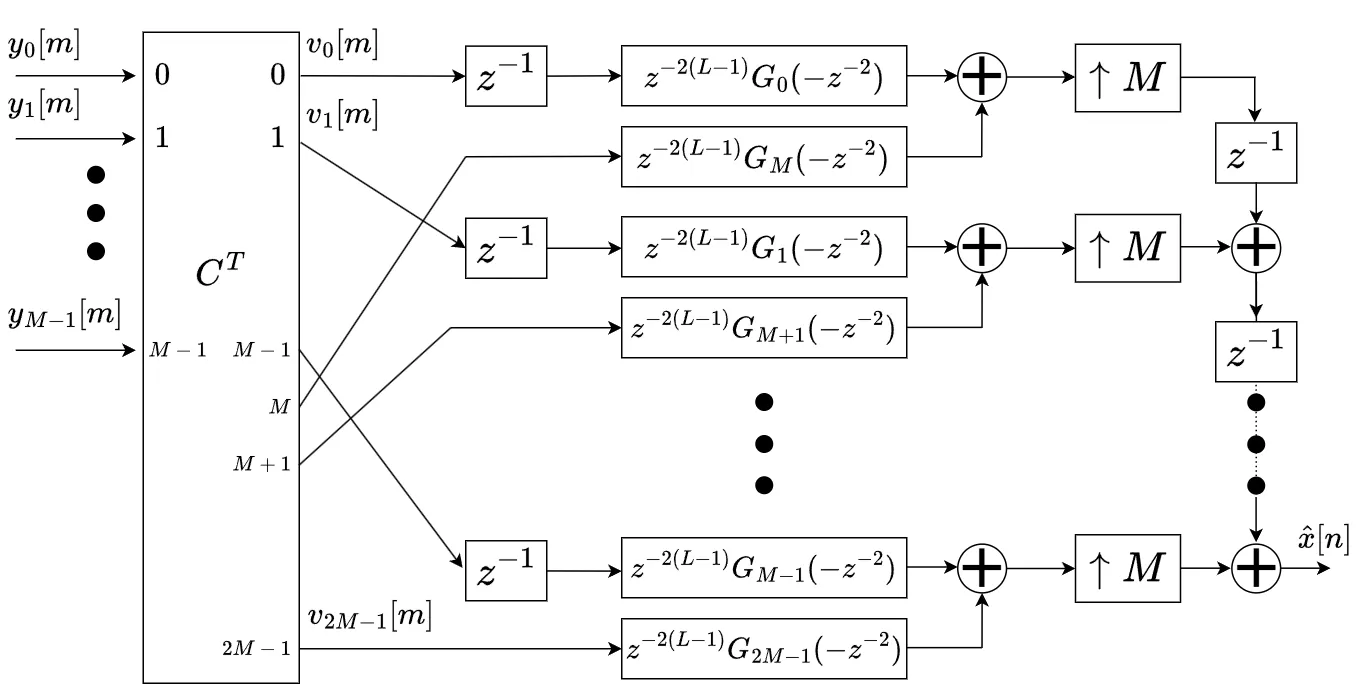
${\mathsf N}_{\mathsf i \mathsf k}\ $について

(8)式で使用する$\ {\mathsf N}_{\mathsf i \mathsf k}\ $も$\ c_{ki}\ $に相当するものであるため、${\mathsf N}_{\mathsf i \mathsf k}\ $と$\ {\mathsf M}_{\mathsf i \mathsf k}\ $は同じ計算式になるはずですが、以下のように微妙に異なっています(iとkの違いは無視してください)。

$$
\begin{align}
{\mathsf M}_{\mathsf i \mathsf k} &= \cos{\left(\frac{\mathsf \pi}{64}(2 \mathsf i+1)(\mathsf k-16)\right)} \\[5pt] {\mathsf N}_{\mathsf i \mathsf k} &= \cos{\left(\frac{\mathsf \pi}{64}(2 \mathsf k+1)(\mathsf i+16)\right)}
\end{align}
$$

${\mathsf N}_{\mathsf i \mathsf k}\ $を式変形すると$\ {\mathsf M}_{\mathsf i \mathsf k}\ $との関係性がわかります。

$\cos(\theta)=\cos(-\theta)\ $より、

$$
\begin{align}
{\mathsf N}_{\mathsf i \mathsf k} &= \cos{\left(\frac{\mathsf \pi}{64}(2 \mathsf k+1)(\mathsf i+16)\right)} \\[5pt] &= \cos{\left(\frac{\mathsf \pi}{64}(2 \mathsf k+1)(-\mathsf i-16)\right)} \tag{18}\\[5pt] \end{align}
$$

それから、$-\cos(\theta+(2k+1)\pi)=\cos(\theta)\ $より、

$$
\begin{align}
{\mathsf N}_{\mathsf i \mathsf k} &= \cos{\left(\frac{\mathsf \pi}{64}(2 \mathsf k+1)(-\mathsf i-16)\right)} \\[5pt] &= -\cos{\left(\frac{\mathsf \pi}{64}(2 \mathsf k+1)(64-\mathsf i-16)\right)} \\[5pt] &= -{\mathsf M}_{\mathsf k,64-\mathsf i} \tag{19}
\end{align}
$$

i が逆順であり、符号が逆になることがわかると思います。

また、${\mathsf i}=0\ $では以下の式のようになります。

$$
{\mathsf N}_{\mathsf 0, \mathsf k} = -{\mathsf M}_{\mathsf k,64} = {\mathsf M}_{\mathsf k,0} \tag{20}
$$

シンセサイザのフィルタ係数

${\mathsf N}_{\mathsf i \mathsf k} $が上記のようになるため、${\mathsf V}_{\mathsf i}\ $と$\ v_{i}\ $の対応は以下のようになります。

$$
\begin{align}
{\mathsf V}_{\mathsf i} &\leftrightarrow -v_{64-i} \hspace{1em} (i=1,\cdots,63) \tag{21}\\[5pt] {\mathsf V}_{0} &\leftrightarrow v_{0} \hspace{1em} (i=0) \tag{22}
\end{align}
$$

シンセサイザではアナライザで使用したフィルタと逆順のフィルタを畳み込む必要がありますが、なぜかMP3では$\ {\mathsf C}_{\mathsf i}\ $と$\ {\mathsf D}_{\mathsf i}$で同じ形のフィルタとなります（大きさが違うだけ）。

これは、(21)式と(22)式からMP3では以下の模式図のようにシンセサイザのフィルタ係数を逆順にさせているからです(m=0は除く)。

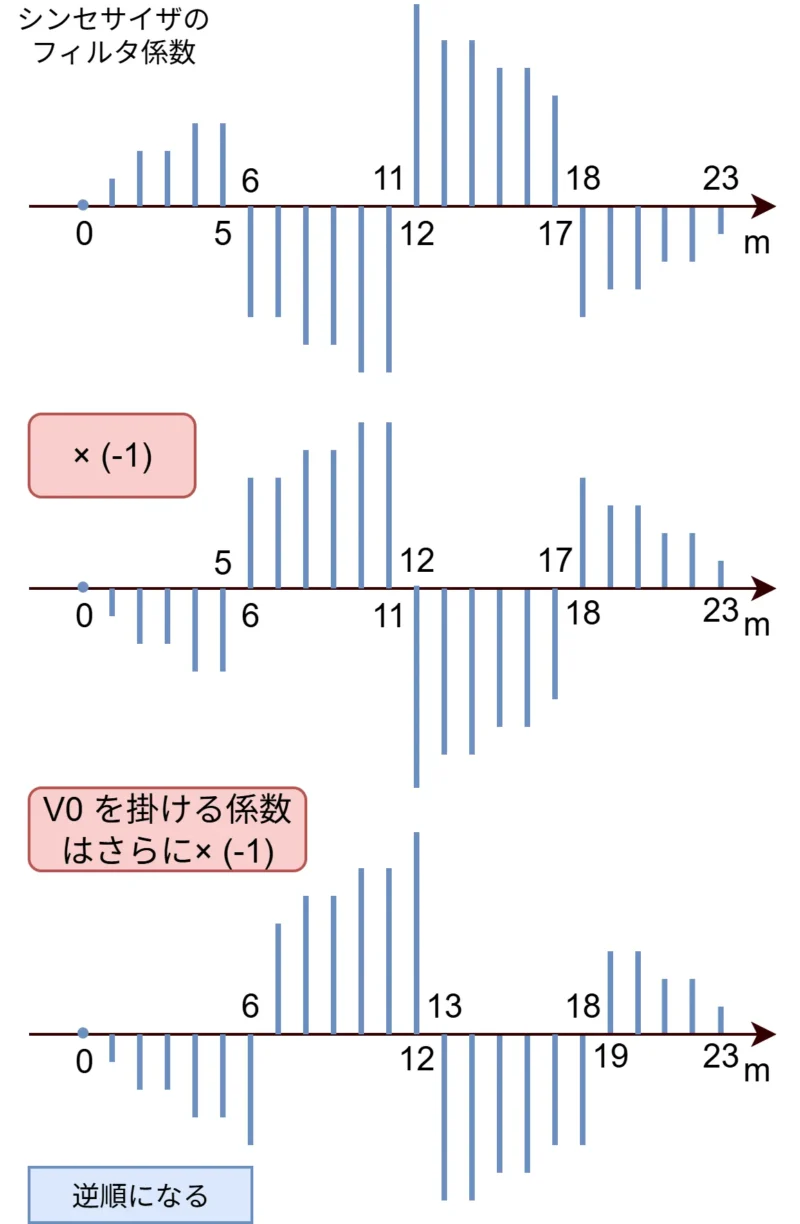
正直いって、${\mathsf N}_{\mathsf i, \mathsf k}\ $を使う理由を理解するのにかなり時間がかかったため、$\ {\mathsf D}_{\mathsf i}\ $は最初からアナライザフィルタの逆順にしておいて欲しかったです。

シンセサイザのフィルタ係数の大きさ

シンセサイザのフィルタ係数$\ {\mathsf D}_{\mathsf i}\ $についてはアナライザのフィルタ係数$\ {\mathsf C}_{\mathsf i}\ $の大きさの約 M=32倍となっています。

これは、MP3のフィルタバンクについての(14)式(以下の式)から、シンセサイザのフィルタ係数はアナライザのフィルタ係数のM倍でなければ、復元信号が元信号と同じ大きさにならないからです。

$$
\hat{X}(z) = \frac{1}{M} X(z) \sum_{k=0}^{M-1} H_{k}(z)F_{k}(z)
$$

プログラム

ソースコード

MP3のフィルタバンクで帯域分割信号を作成後、復元信号を合成するソースコードを作成しました。アナライザに問題ないか確認するために途中で各バンドのRMSを計算しています。

import numpy as np
import soundfile as sf
import matplotlib.pyplot as plt

def mp3_analysis_filter_bank( data, N, M ):
    """
    MP3のフィルタバンクを出力

    Parameters
    ----------
    data (np.array) : 入力信号
    N (int) : フィルタの次数
    M (int) : フィルタバンクの数

    Returns
    -------
    s (np.array) : フィルタバンクの出力信号

    """

    # 変数用意
    L = (N+1)//(2*M)
    x = np.zeros( N+1, dtype=np.float64 )  # バッファ
    z = np.zeros( N+1, dtype=np.float64 )  # バッファ
    y = np.zeros( 2*M, dtype=np.float64 )  # バッファ
    data_len = data.shape[0]   # データ長取得
    iter_num = data_len // M   # ループ回数
    s = np.zeros((iter_num, M), dtype=np.float64 )  # 出力信号

    # M_ik をあらかじめ計算
    M_ik = np.zeros((M,2*M), dtype=np.float64)
    for i in range( M ):
        for k in range( 2*M ):
            M_ik[i,k] = (2*i+1)*(k-M/2)*(np.pi/(2*M))
    M_ik = np.cos( M_ik )

    # フィルタ係数 C_i をあらかじめ取得
    C = np.genfromtxt("filtercoef_analysis.txt")   # フィルタ係数取得
    C = C[:,1]

    for iter in range( iter_num ):

        # データ取得
        x[M:N+1] = x[0:N+1-M]
        x[M-1::-1] = data[iter*M:(iter+1)*M]

        # フィルタ係数を乗算
        z = x * C

        # フィルタバンクの出力計算
        for i in range( 2*M ):
            y[i] = np.sum(z[i:N+1:(2*M)]) 

        for i in range( M ):
            s[iter,i] = np.sum( M_ik[i,:] * y )

    return s

def mp3_synthesis_filter_bank( data, N, M ):
    """
    MP3のフィルタバンクを出力

    Parameters
    ----------
    data (np.array) : フィルタバンク信号
    N (int) : フィルタの次数
    M (int) : フィルタバンクの数

    Returns
    -------
    s (np.array) : 復元信号

    """

    # 変数用意
    L = (N+1)//(2*M)
    v = np.zeros( 2*(N+1), dtype=np.float64 )
    u = np.zeros(   (N+1), dtype=np.float64 )
    iter_num = data.shape[0] # ループ回数
    s = np.zeros( iter_num*M, dtype=np.float64 )

    # N_ik をあらかじめ計算
    N_ik = np.zeros((2*M,M), dtype=np.float64)
    for i in range( 2*M ):
        for k in range( M ):
            N_ik[i,k] = (2*k+1)*(i+M/2)*(np.pi/(2*M))
    N_ik = np.cos( N_ik )

    # フィルタ係数 D_i をあらかじめ取得
    D = np.genfromtxt("filtercoef_synthesis.txt")   # フィルタ係数取得
    D = D[:,1]

    for iter in range( iter_num ):

        # v を計算
        v[2*M:2*(N+1)] = v[0:2*(N+1)-2*M]
        for i in range( 2*M ):
            v[i] = np.sum( N_ik[i,:] * y[iter,:] )

        # u に格納
        for i in range( L ):
            u[i*(2*M):i*(2*M)+M] = v[i*(4*M):i*(4*M)+M]
            u[i*(2*M)+M:(i+1)*(2*M)] = v[i*(4*M)+(3*M):i*(4*M)+(4*M)]

        # フィルタ係数を乗算
        w = u * D

        # 復元信号を計算
        for i in range( M ): 
            s[iter*M+i] = np.sum( w[i:(N+1):M] )

    return s 

# パラメータ
N = 511   # フィルタ次数
M = 32    # フィルタバンクの数

# WAV を読み込む
s, fs = sf.read('input.wav')
s_len = s.shape[0]

# フィルタバンク出力
y = mp3_analysis_filter_bank( s[:s_len//10], N, M )

# 各バンドのRMSを計算
rms_dB = np.zeros(M, dtype=np.float64)
for k in range(M):
    rms = np.sqrt(np.mean(np.square(y[:,k])))
    rms_dB[k] = 20 * np.log10(rms)

# グラフをプロット
fig, ax = plt.subplots()
ax.plot( rms_dB, 'o-')
ax.set_xlabel('band')
ax.set_ylabel('RMS [dB]')
plt.savefig("band_RMS.png")

# 復元信号を出力
s_hat = mp3_synthesis_filter_bank( y, N, M )
sf.write("synthesis.wav", s_hat, fs, subtype="PCM_24") # 書き込み

5～57行目：アナライザで帯域分割する関数です。

59～112行目：シンセサイザで復元信号を合成する関数です。

125～129行目：各バンドのRMSを計算しています。

実行方法

(1) プログラムを実行するディレクトリにソースコード(polyphase_filterbank.py)とWAVファイルを格納する。

(2) ソースコード114～116行目のパラメータを修正する。

# パラメータ
N = 511   # フィルタ次数
M = 32    # フィルタバンクの数

(3) 以下のコマンドで python を実行すると、各バンドのRMSのグラフ（band_RMS.png）と復元信号(synthesis.wav)が出力される。

$ python polyphase_filterbank.py

動作確認

上記のソースコードを使用して、5kHzのサイン波を入力して、RMSのグラフを出力した結果は以下のようになりました。

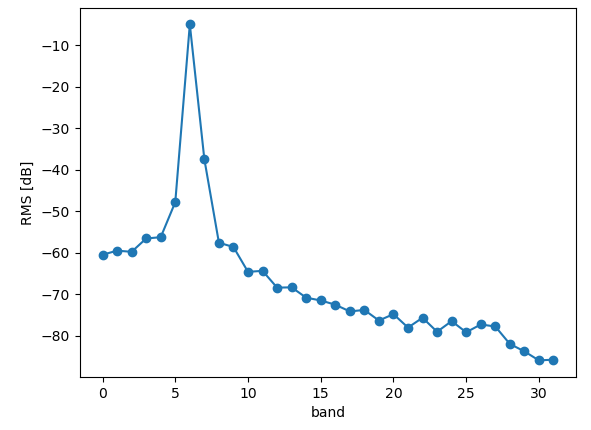
5kHz(Fs=48kHz)の場合、6番か7番のバンドに入力されるため、アナライザの実装は問題なさそうです。

440Hzのサイン波を入力して復元した信号のスペクトルと波形は以下のようになりました。

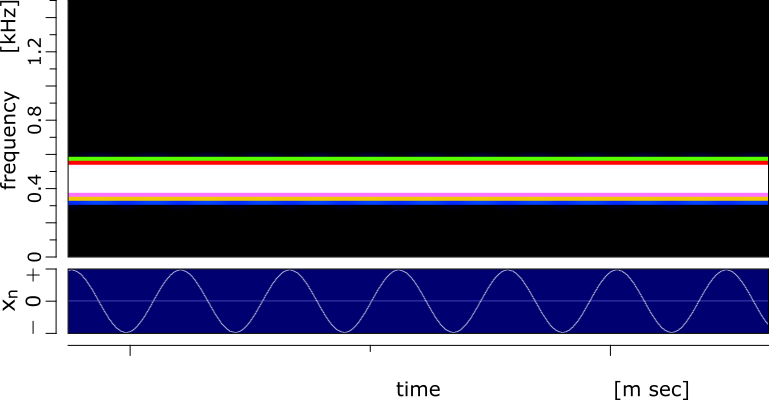
440Hzのサイン波のスペクトルと波形が綺麗に出力されているため、シンセサイザも問題なさそうです。

おわりに

本記事では、MP3のフィルタバンクを実装しました。実装は簡単にできましたが、各操作の意味を理解するのにかなりの時間を費やしました。

次はMP3のもう一つの周波数解析である MDCT について調べようかなと思います。ただ、フィルタバンクを調べるだけでも半年以上かかったため、こちらも結構な時間を必要としそうで不安です。

■参考文献
[1] ISO/IEC JTC1/SC29/WG11 MPEG, IS11172-3 "Information Technology - Coding of Moving Pictures and Associated Audio for Digital Storage Media at up to About 1.5 Mbit/s Part 3: Audio," 1992, ("MPEG1").

MP3のフィルタバンクを実装

MP3における実装手順

アナライザ

データ取得

フィルタ係数を乗算

帯域分割信号を生成

シンセサイザ

\({\mathsf V}_{\mathsf i}\ \)を計算

\({\mathsf V}_{\mathsf i}\ \)を\(\ {\mathsf U}_{\mathsf i}\ \)に詰める

フィルタ係数を乗算

復元信号を合成

実装の解説

アナライザの計算

アナライザのフィルタ係数

\({\mathsf M}_{\mathsf i \mathsf k}\ \)について

1. 係数2について

2. N/2の削除

3. \((-1)^{i}\pi/4\ \)の変更

シンセサイザの計算

\({\mathsf N}_{\mathsf i \mathsf k}\ \)について

シンセサイザのフィルタ係数

シンセサイザのフィルタ係数の大きさ

プログラム

ソースコード

実行方法

動作確認

おわりに