本記事ではMP3で使われているフィルタバンクであるコサイン変調フィルタバンクを説明します。
コサイン変調フィルタバンク(Cosine Modulation Filter Bank)については疑似QMFバンク(Pseudo quadrature mirror filter Bank)とも呼ばれます。
MP3のフィルタバンク
MP3ではコサイン変調フィルタバンクが周波数解析で使用されます。
コサイン変調フィルタバンクのブロック図は以下です。\(M\ \)はフィルタバンクの数です。
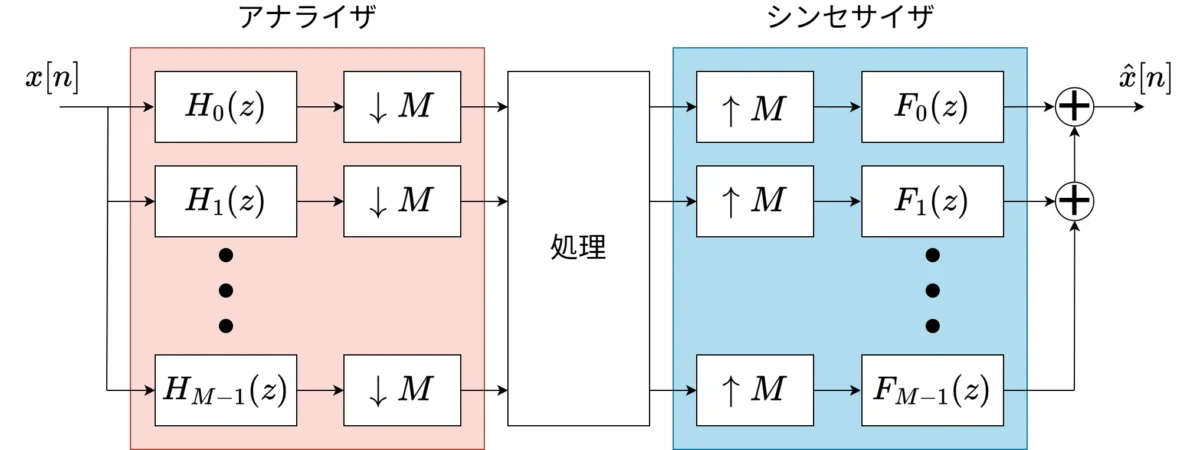
↓M はデシメータ、↑M はインタポレータです。
\(H_{k}(z)\), \(F_{k}(z)\ \)のフィルタ係数\(\ h_{k}\), \(f_{k}\ \)は以下のように表されます。
\begin{align}
h_{k}[n] &= 2\ p_{0}[n]\cos{\left(\frac{\pi}{M}\left(k+\frac{1}{2}\right)\left(n-\frac{N}{2}\right)+\theta_{k}\right)} \tag{1}\\[5pt] f_{k}[n] &= 2\ p_{0}[n]\cos{\left(\frac{\pi}{M}\left(k+\frac{1}{2}\right)\left(n-\frac{N}{2}\right)-\theta_{k}\right)} \tag{2}
\end{align}
$$
ここで、\(N\ \)はフィルタの次数、\(\theta_{k}=(-1)^{k}(1/4)\ \)、\(p_{0}[n]\ \)はプロトタイプフィルタ\(\ P_{0}(z)\ \)のフィルタ係数です。
\(H_{k}(z)\), \(F_{k}(z)\ \)については\(\ P_{0}(z)\ \)をコサイン変調でシフトさせたものとなっており、プロトタイプフィルタ\(\ P_{0}(z)\ \)を決めれば残りのフィルタは設計する必要がないのがコサイン変調フィルタバンクの特徴となります。
フィルタの導出
(1)式と(2)式の導出方法について説明します[1]。導出過程はかなり長いです。
周波数シフト
フーリエ変換には以下のように時間領域の信号に複素指数関数を掛けると周波数領域で周波数シフトする性質があります。
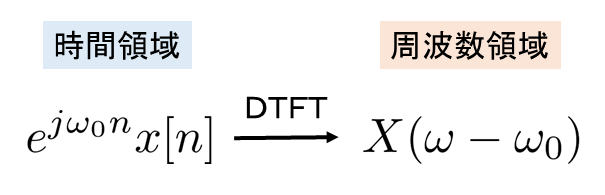
この性質から\(\ p_{0}[n]\ \)に以下のように\(\ 2\cos\ \)を掛けると、
\begin{align}
&\ 2p_{0}[n]\cos{\left(\frac{\pi}{M}\left(k+\frac{1}{2}\right)n\right)} \\[5pt] &= 2p_{0}[n]\frac{\exp{\left(j\frac{\pi}{M}\left(k+\frac{1}{2}\right)n\right)}+\exp{\left(-j\frac{\pi}{M}\left(k+\frac{1}{2}\right)n\right)}}{2}\\[5pt] &= \exp{\left(j\frac{\pi}{M}\left(k+\frac{1}{2}\right)n\right)}p_{0}[n]+\exp{\left(-j\frac{\pi}{M}\left(k+\frac{1}{2}\right)n\right)}p_{0}[n]\\[5pt] &\xrightarrow{\rm DTFT} P_{0}\left(\omega-\frac{\pi}{M}\left(k+\frac{1}{2}\right)\right) + P_{0}\left(\omega+\frac{\pi}{M}\left(k+\frac{1}{2}\right)\right) \\[5pt] &= P_{0}\left(z \cdot \exp{\left(-j\frac{\pi}{M}\left(k+\frac{1}{2}\right)\right)}\right) + P_{0}\left(z \cdot \exp{\left(j\frac{\pi}{M}\left(k+\frac{1}{2}\right)\right)}\right) \\[5pt] &= Q_{k}(z) + Q_{2M-1-k}(z)\tag{3}
\end{align}
$$
となり、周波数領域で\(\ P_{0}(z)\ \)が周波数シフトされ、下図のように帯域を等分割するフィルタ\(\ Q_{k}(z)\ \)を作成できます。
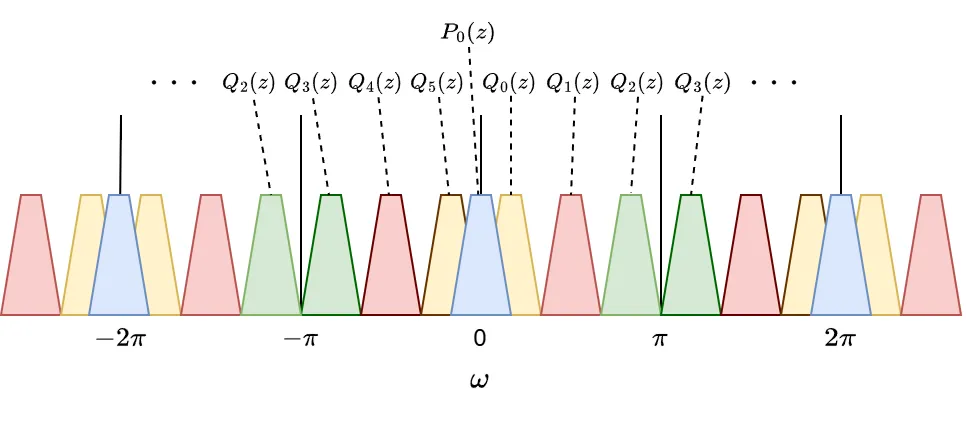
\(Q_{k}(z), Q_{2M-1-k}(z)\ \)の振幅応答は\(\ \omega=0\ \)で互いに鏡像（\(|Q_{k}(\omega)|=|Q_{2M-1-k}(-\omega)|\)）となります。
\begin{align}
&\ P_{0}\left(z \cdot \exp{\left(j\frac{\pi}{M}\left(k+\frac{1}{2}\right)\right)}\right)\\[5pt] &= P_{0}\left(z \cdot \exp{\left(-j\left(2\pi-\frac{\pi}{M}\left(k+\frac{1}{2}\right)\right)\right)}\right)\\[5pt] &= P_{0}\left(z \cdot \exp{\left(-j\frac{\pi}{M}\left(2M-k-1+\frac{1}{2}\right)\right)}\right)\\[5pt] &= Q_{2M-1-k}(z)
\end{align}
$$
エイリアシング除去条件
上記の周波数シフトで帯域分割はできましたが、復元した信号\(\ \hat{x}[n]\ \)が処理ブロックで何もしないときに元の信号に戻りません。
コサイン変調フィルタバンクでは復元信号が完全に元の信号には戻りませんが、元の信号に近似するようにはします。
まず、\(F_{k}(z)\ \)の出力において隣り合うエイリアシングを除去するようにします。
\(F_{k}(z)\ \)の出力までの数式を以下に示します。
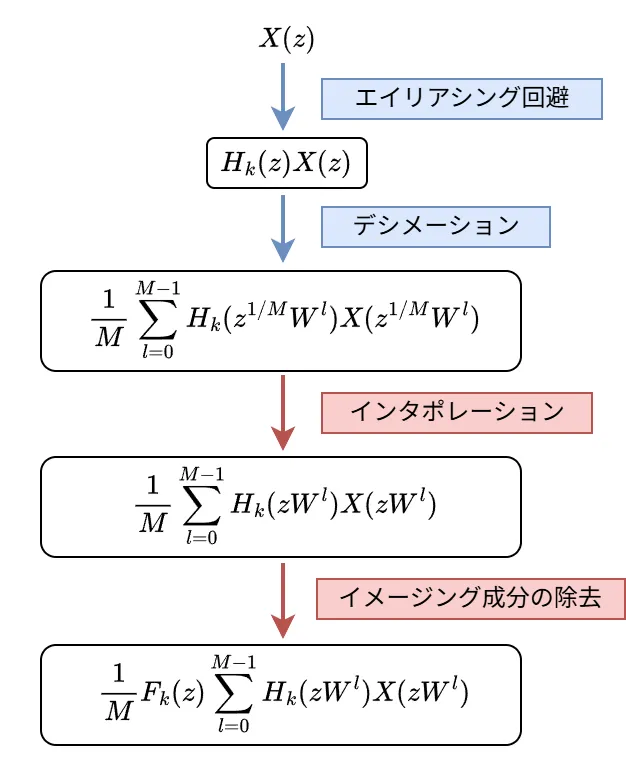
\(W=e^{-j 2\pi/M}\ \)となります。
各数式のグラフは下図のようになります。
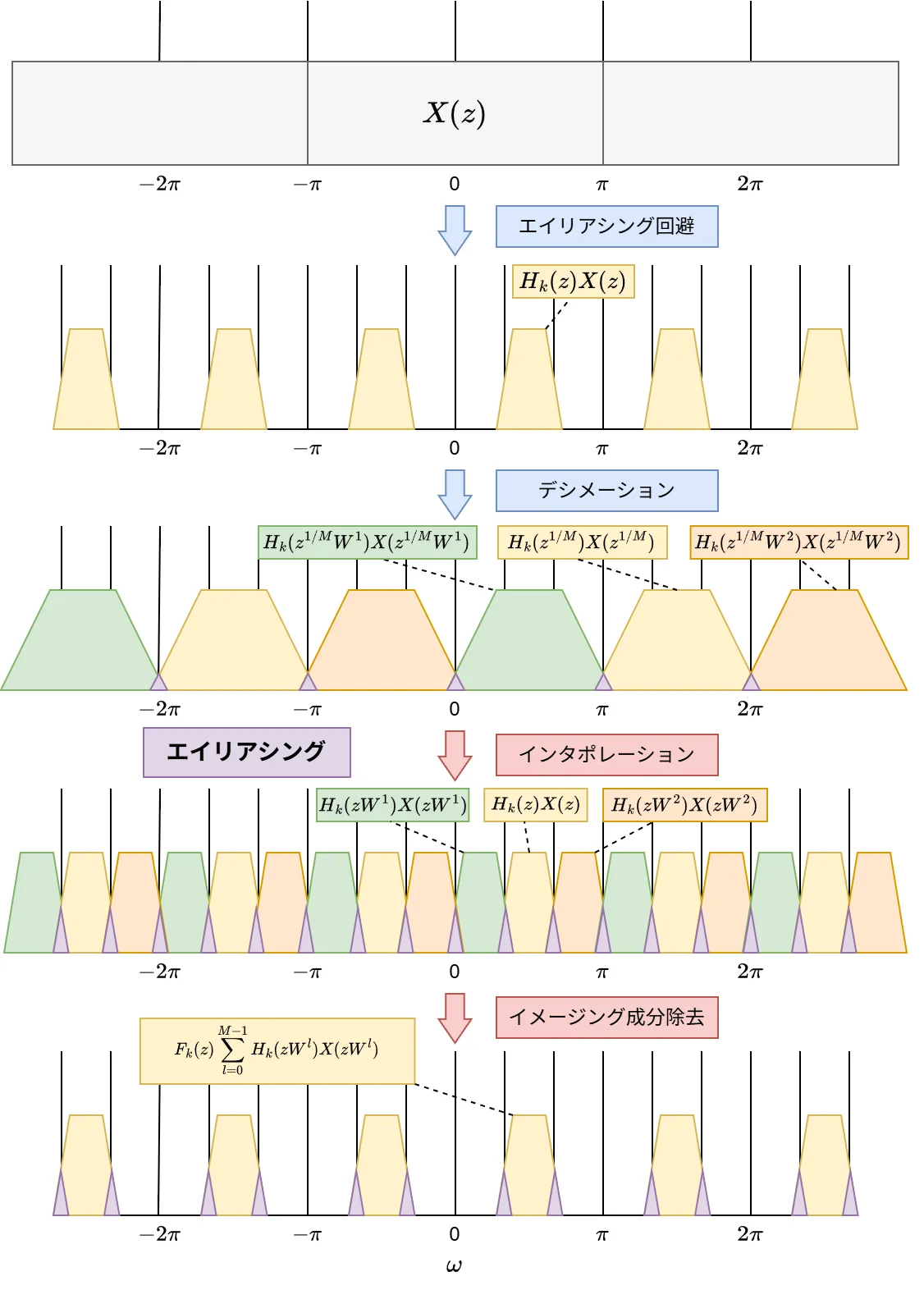
上図のように\(\ F_{k}(z)\ \)の出力にはエイリアシング（紫の部分）が含まれています。このエイリアシングを打ち消すような\(\ H_{k}(z), F_{k}(z)\ \)を求めます。
・\(H_{k}(z^{1/M}W^{l})X(z^{1/M}W^{l})\ \)：\(H_{k}(z)X(z)\ \)を原点中心にX軸方向にM倍拡大して、\(2\pi l\ \)だけX軸方向に平行移動したグラフ。
・\(H_{k}(zW^{l})X(zW^{l}) \)：\(H_{k}(z)X(z)\ \)を\(\ 2\pi l/M\ \)だけX軸方向に平行移動したグラフ。
はじめに、\(\ H_{k}(z), F_{k}(z)\ \)を以下のように表現します。
\begin{align}
H_{k}(z) &= a_{k}U_{k}(z) + a_{k}^{*}V_{k}(z) \tag{4}\\[5pt] F_{k}(z) &= b_{k}U_{k}(z) + b_{k}^{*}V_{k}(z) \tag{5}
\end{align}
$$
ここで、\(a_{k}, b_{k}\ \)は絶対値が1である定数（複素数）であり、\(\ U_{k}(z), V_{k}(z)\ \)は以下とします。
\begin{align}
U_{k}(z) &= c_{k}Q_{k}(z) \tag{6} \\[5pt] V_{k}(z) &= c_{k}^{*}Q_{2M-1-k}(z) \tag{7}
\end{align}
$$
\(c_{k} \)も絶対値が1である定数（複素数）です。
\(M=3,\ k=1\ \)の場合、\(F_{k}(z)\)の負の周波数部分\(\ b_{k}^{*}V_{k}(z)\ \)のエイリアシング（Aの部分）は下図のようになります。
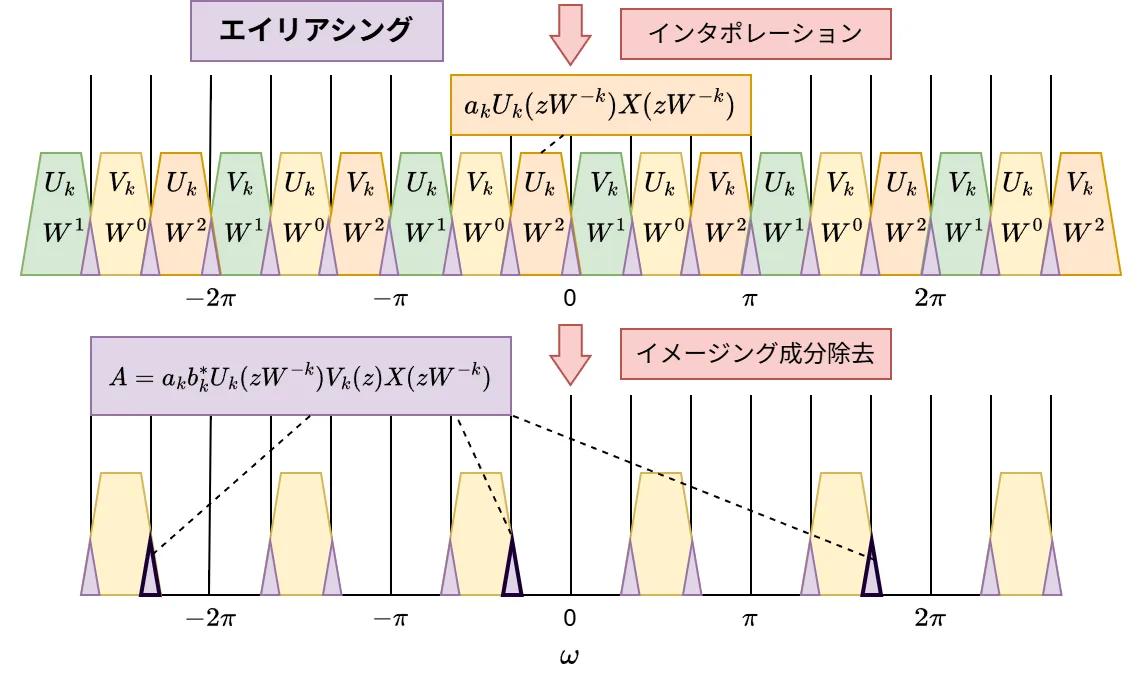
一般的にA部分の式は以下です。
A=a_{k}b_{k}^{*}U_{k}(zW^{-k})V_{k}(z)X(zW^{-k}) \tag{8}
$$
\(W^{(M-k)}=W^{-k}\) であることに注意です。
次に、\(F_{k-1}(z)\)の負の周波数部分のエイリアシング（Bの部分）は下図のようになります。
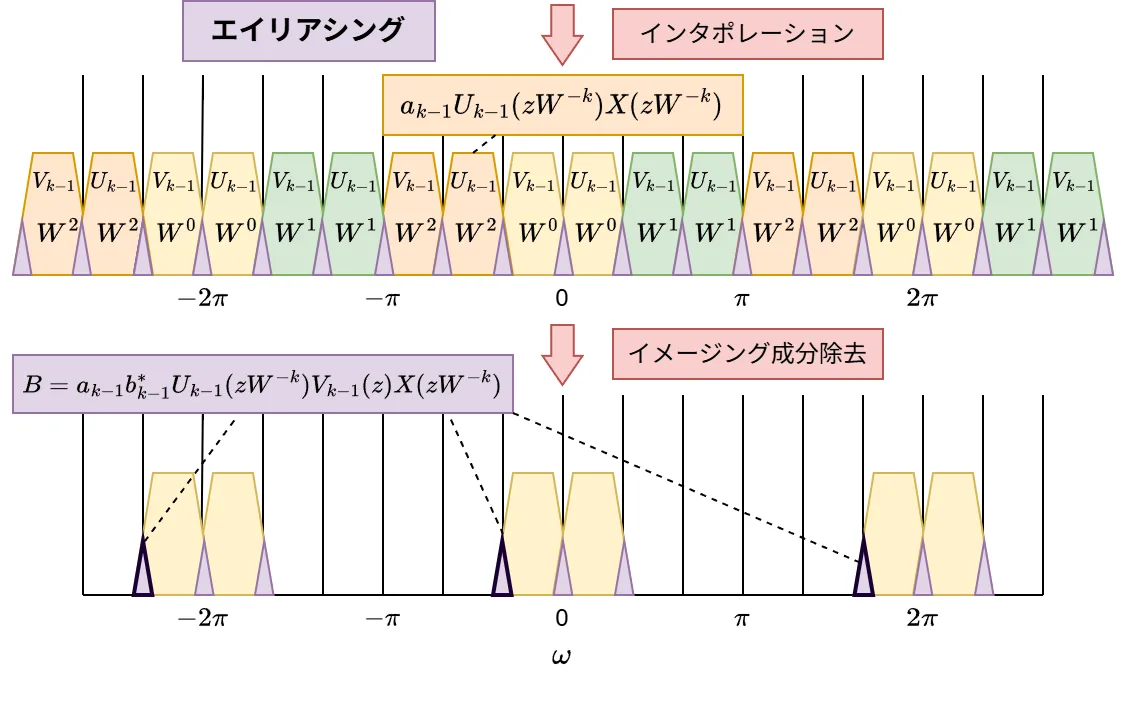
一般的にB部分の式は以下です。
B=a_{k-1}b_{k-1}^{*}U_{k-1}(zW^{-k})V_{k-1}(z)X(zW^{-k}) \tag{9}
$$
この A と B の部分を足し合わせたとき、つまり、
\begin{align}
&A+B = 0 \\[5pt] &a_{k}b_{k}^{*}U_{k}(zW^{-k})V_{k}(z)X(zW^{-k}) \\[5pt] &\hspace{1em} + a_{k-1}b_{k-1}^{*}U_{k-1}(zW^{-k})V_{k-1}(z)X(zW^{-k}) = 0 \tag{10}
\end{align}
$$
が成り立てばエイリアシングが打ち消される。
\(U_{k}(z)\) と\(V_{k}(z)\)の定義と\(|c_{k}|=|c_{k-1}|=1\)より、
(a_{k}b_{k}^{*}+a_{k-1}b_{k-1}^{*})V_{k-1}(z)V_{k}(z)=0 \tag{11}
$$
と書き直されるため、\(1\leq k \leq M-1\)において、
a_{k}b_{k}^{*}＝-a_{k-1}b_{k-1}^{*} \tag{12}
$$
となるように定数を設定すれば、エイリアシングを打ち消すことができる。
今回は、\(F_{k}(z)\)の負の周波数部分からエイリアシングの除去条件を導いたが、正の周波数部分\(b_{k}U_{k}(z)\)のエイリアシングから考えることでも同様の条件を導くことができる。
(11)式の導出：(10)式から(11)式の計算過程は以下です。
まず、
\begin{align}
V_{k}(z) &= c_{k}^{*}Q_{2M-1-k}(z) \\[5pt] &= c_{k}^{*}P_{0}(z W^{(2M-k-1+0.5)/2}) \\[5pt] &= c_{k}^{*} P_{0}(zW^{-k} W^{(k-0.5)/2})
\end{align}
$$
より
\begin{align}
U_{k-1}(zW^{-k}) &= c_{k-1}Q_{k-1}(zW^{-k}) \\[5pt] &= c_{k-1} P_{0}(zW^{-k} W^{(k-0.5)/2}) \\[5pt] &= c_{k-1} \frac{V_{k}(z)}{c_{k}^{*}} \\[5pt] &= c_{k}c_{k-1} V_{k}(z) \\[5pt] \end{align}
$$
また、
V_{k-1}(z) = c_{k-1}^{*} P_{0}(zW^{-k} W^{(k+0.5)/2})
$$
より
\begin{align}
U_{k}(zW^{-k}) &= c_{k}Q_{k}(zW^{-k}) \\[5pt] &= c_{k} P_{0}(zW^{-k} W^{(k+0.5)/2}) \\[5pt] &= c_{k} \frac{V_{k-1}(z)}{c_{k-1}^{*}} \\[5pt] &= c_{k} c_{k-1} V_{k-1}(z)
\end{align}
$$
したがって、(10)式は以下のように変更される。
(a_{k}b_{k}^{*}+a_{k-1}b_{k-1}^{*}) c_{k}c_{k-1} V_{k-1}(z)V_{k}(z)X(zW^{-k}) = 0
$$
\(X(zW^{-k})\neq 0,\ c_{k}\neq 0,\ c_{k-1}\neq 0\ \)より(11)式が導かれる。
(a_{k}b_{k}^{*}+a_{k-1}b_{k-1}^{*}) V_{k-1}(z)V_{k}(z) = 0 \tag{11}
$$
位相歪みの除去
復元信号\(\ \hat{x}[n]\ \)のz変換である\(\ \hat{X}(z)\ \)は以下のように表せます。
\begin{align}
\hat{X}(z) &= \frac{1}{M}\sum_{k=0}^{M-1} F_{k}(z) \sum_{l=0}^{M-1}H_{k}(zW^{l})X(zW^{l}) \\[5pt] &= \frac{1}{M}\sum_{l=0}^{M-1}X(zW^{l})\sum_{k=0}^{M-1}H_{k}(zW^{l})F_{k}(z) \tag{13}
\end{align}
$$
隣り合うエイリアシングは打ち消され、隣り合わないエイリアシングは無視できるものとすると、\(1\leq l \leq M-1\ \)で\(\ X(zW^{l})\ \)が削除され、\(\ \hat{X}(z)\ \)は以下の式で表される。
$$
\hat{X}(z) = \frac{1}{M} X(z) \sum_{k=0}^{M-1} H_{k}(z)F_{k}(z) \tag{14}
$$
ここで、(14)式に含まれている以下の関数\(\ T(z)\ \)は歪み関数と呼ばれます。
$$
T(z) = \frac{1}{M} \sum_{k=0}^{M-1} H_{k}(z)F_{k}(z) \tag{15}
$$
次は、位相歪みをなくすため、この歪み関数\(\ T(z)\ \)が線形位相となるように\(\ a_{k}, b_{k}, c_{k}\ \)を決めていきます。
線形位相条件の書き換え
\(T(z)\ \)が線形位相となることと、以下の式が成り立つことは等価となります。
$$
f_{k}[n] = h_{k}[N-n] \tag{16}
$$
z変換した場合、以下となります。
$$
F_{k}(z) = z^{-N}H_{k}(z^{-1}) \tag{17}
$$
そのため、\(\ a_{k}, b_{k}, c_{k}\ \)を(17)式が成立するように決めていきます。
\(c_{k}\ \)の決め方
まず、\(U_{k}(z), V_{k}(z)\ \)が線形位相となるように\(\ c_{k}\ \)を決めていきます。
\(P_{0}(z)\ \)を線形位相フィルタとすると、フィルタ係数は左右対称な形になり、\(p_{0}[n]=p_{0}[N-n]\ \)となります。
このとき、\(N\ \)を奇数とすると、\(\ P_{0}(z)\ \)は以下のように表せます。
\begin{align}
&P_{0}(\omega) \\[5pt] &=\sum_{n=0}^{N} p_{0}[n] e^{-jn\omega} \\[5pt] &= e^{-jN\omega/2} \sum_{n=0}^{N} p_{0}[n] e^{-j(n-N/2)\omega} \\[5pt] &= e^{-jN\omega/2} \left(2\sum_{m=0}^{(N-1)/2} p_{0}[m] \frac{e^{j(m-N/2)\omega}+e^{-j(m-N/2)\omega}}{2} \right) \\[5pt] &= e^{-jN\omega/2} \left(2\sum_{m=0}^{(N-1)/2} p_{0}[m] \cos{((m-N/2)\omega)} \right) \\[5pt] &= e^{-jN\omega/2} P_{R}(\omega) \tag{18}\\[5pt] \end{align}
$$
ここで、\(P_{R}(\omega)\ \)は実数をとる関数である。
(6)式より、
\begin{align}
&U_{k}(\omega) \\[5pt] &= c_{k}Q_{k}(\omega) \\[5pt] &= c_{k} P_{0}\left(\omega-\frac{\pi}{M}\left(k+\frac{1}{2}\right)\right) \\[5pt] &= c_{k} e^{-jN\left(\omega-\frac{\pi}{M}\left(k+\frac{1}{2}\right)\right)/2}P_{R}\left(\omega-\frac{\pi}{M}\left(k+\frac{1}{2}\right)\right) \tag{19}
\end{align}
$$
が得られる。ここで、
$$
c_{k} = e^{-jN\frac{\pi}{M}\left(k+\frac{1}{2}\right)/2} \tag{20}
$$
とすることで、
U_{k}(\omega) = e^{-jN\omega/2} P_{R}\left(\omega-\frac{\pi}{M}(k+\frac{1}{2})\right) \tag{21}
$$
となる。\(P_{R}(\omega)\ \)は実数であるため、\(U_{k}(z)\ \)の位相特性は\(\ \phi(\omega)=-N\omega/2\ \)となり、\(P_{0}(z)\ \)と同じ線形位相特性となります。
このとき、\(V_{k}(z)\ \)についても同様の線形位相特性となります。
\(b_{k}\ \)の決め方
\(c_{k}\ \)を決めたことにより\(\ U_{k}(z)\ \)と\(\ V_{k}(z)\ \)が線形位相となったので以下のように表せます。
$$
\begin{align}
U_{k}^{*}(z) = z^{N}U_{k}(z) \tag{22}\\[5pt]
V_{k}^{*}(z) = z^{N}V_{k}(z) \tag{23}
\end{align}
$$
したがって、
\begin{align}
z^{-N}H_{k}(z^{-1}) &= z^{-N}H_{k}^{*}(z) \\[5pt] &= z^{-N}(a_{k}U_{k}(z)+a_{k}^{*}V_{k}(z))^{*} \\[5pt] &= z^{-N}(a_{k}^{*}U_{k}^{*}(z)+a_{k}V_{k}^{*}(z)) \\[5pt] &= a_{k}^{*}z^{-N}U_{k}^{*}(z)+a_{k}z^{-N}V_{k}^{*}(z) \\[5pt] &= a_{k}^{*}U_{k}(z)+a_{k}V_{k}(z) \tag{24}
\end{align}
$$
となるため、
$$
b_{k} = a_{k}^{*} \tag{25}
$$
であれば、(17)式が成立して、\(T(z)\ \)が線形位相特性となります。
複素係数フィルタの線形位相特性：(22)式と(24)式について説明します。
線形位相特性であることから、フィルタ係数は\(\ u[n]=u^{*}[N-n]\ \)となり、
$$
\begin{align}
z^{N}U_{k}(z) &= z^{N}\sum_{n=0}^{N} u[n]z^{-n} \\[5pt]
&= \sum_{n=0}^{N} u^{*}[N-n]z^{N-n} \\[5pt]
&= \sum_{m=0}^{N} u^{*}[m]z^{m} \\[5pt]
&= U_{k}^{*}(z)
\end{align}
$$
また、\(\ H_{k}(z^{-1})=H_{k}^{*}(z)\ \)については、\(h[n]\ \)が実数より、
$$
\begin{align}
H_{k}(z^{-1}) &= \sum_{n=0}^{N} h[n]z^{n} \\[5pt]
&= \sum_{n=0}^{N} h^{*}[n]z^{n} \hspace{1em}(h[n]=h^{*}[n])\\[5pt]
&= H_{k}^{*}(z)
\end{align}
$$
\(a_{k}\ \)の決め方
\(c_{k}, b_{k}\ \)を決定したことにより、\(T(z)\ \)は線形位相特性となりますが、\(T(z)\ \)の振幅歪みがあるので、それを低減するように\(\ a_{k}\ \)を決めていきます。
(25)式より
\begin{align}
&MT(z) \\[5pt] &= \sum_{k=0}^{M-1} H_{k}(z)F_{k}(z) \\[5pt] &= \sum_{k=0}^{M-1} (a_{k}U_{k}(z)+a_{k}^{*}V_{k}(z))(b_{k}U_{k}(z)+b_{k}^{*}V_{k}(z)) \\[5pt] &= \sum_{k=0}^{M-1} U_{k}^{2}(z)+V_{k}^{2}(z)+(a_{k}^2+a_{k}^{*2})U_{k}(z)V_{k}(z) \tag{26}
\end{align}
$$
となります。
また、\(U_{k}(z)V_{k}(z)\ \)については\(\ k=0,\ k=M-1\ \)だけ下図のようにオーバーラップし、その他はオーバーラップしません。
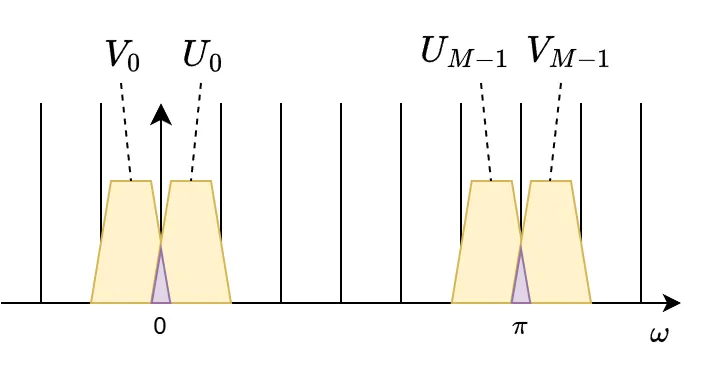
そのため、\(k=0,\ k=M-1\ \)を除いて、\(\ U_{k}(z)V_{k}(z)\simeq 0\ \)とすれば、
\begin{align}
MT(z)\simeq& \ (a_{0}^{2}+a_{0}^{*2})U_{0}(z)V_{0}(z) \\[5pt] &+(a_{M-1}^{2}+a_{M-1}^{*2})U_{M-1}(z)V_{M-1}(z) \\[5pt] &+\sum_{k=0}^{M-1} (U_{k}^{2}(z)+V_{k}^{2}(z)) \tag{27}
\end{align}
$$
と簡略化されます。
(27)式では\(\ U_{0}(z)V_{0}(z), U_{M-1}(z)V_{M-1}(z)\ \)が残り、\(\omega=0, \pi\ \)の周りで歪みが生じるので、これらを消去するように\(\ a_{0}, a_{M-1}\ \)を決めます。
\(a_{0}\ \)について考えると
$$
\begin{align}
a_{0}^{2}+a_{0}^{*2}&=0 \\[5pt]
a_{0}^{2} &= -a_{0}^{*2} \\[5pt]
a_{0}^{4} &= -1 \tag{28}
\end{align}
$$
とすることで\(\ U_{0}(z)V_{0}(z) \) が消去されます。(12)式と(25)式より
$$
\begin{align}
a_{k}b_{k}^{*}&＝-a_{k-1}b_{k-1}^{*} \\[5pt]
a_{k}^{2} &= -a_{k-1}^{2} \\[5pt]
a_{k}^{4} &= a_{k-1}^{4} \tag{29}
\end{align}
$$
なので、
$$
a_{M-1}^{4} = a_{M-2}^{4} \cdots a_{1}^{4}=a_{0}^{4}=-1 \tag{30}
$$
となり、\(\ U_{M-1}(z)V_{M-1}(z) \) も消去されます。
最終的に歪み関数は以下になります。
$$
\begin{align}
T(z) \simeq \frac{1}{M}\sum_{k=0}^{M-1}U_{k}^{2}(z)+V_{k}^{2}(z) \tag{31}
\end{align}
$$
\(a_{k}^{4}=-1\ \)と\(\ a_{k}^{2} = -a_{k-1}^{2}\ \)より、\(a_{k}\ \)は以下のように決定されます。
$$
a_{k} = e^{j\theta_{k}},\hspace{1em} \theta_{k} = (-1)^{k}\frac{\pi}{4} \tag{32}
$$
フィルタ係数の決定
\(a_{k}, b_{k}, c_{k}\ \)の決定より、
\begin{align}
&\ H_{k}(z) \\[5pt] &=\ a_{k}U_{k}(z)+a_{k}^{*}V_{k}(z) \\[5pt] &=\ e^{j\theta_{k}} e^{-jN\frac{\pi}{M}(k+1/2)/2} P_{0}(z\cdot e^{-j\frac{\pi}{M}(k+1/2)}) \\[2pt] &\hspace{1em} + e^{-j\theta_{k}} e^{jN\frac{\pi}{M}(k+1/2)/2} P_{0}(z\cdot e^{j\frac{\pi}{M}(k+1/2)}) \tag{33} \\[5pt] &=\ e^{j\theta_{k}} e^{-jN\frac{\pi}{M}(k+1/2)/2} \sum_{n=0}^{N} p_{0}[n]e^{j\frac{\pi}{M}(k+1/2)n}z^{-n} \\
&\hspace{1em} + e^{-j\theta_{k}} e^{jN\frac{\pi}{M}(k+1/2)/2} \sum_{n=0}^{N} p_{0}[n]e^{-j\frac{\pi}{M}(k+1/2)n}z^{-n} \\[5pt] &=\ \sum_{n=0}^{N} 2p_{0}[n] \cos{\left(\frac{\pi}{M}(k+\frac{1}{2})(n-\frac{N}{2})+\theta_{k}\right)} z^{-n} \tag{34}
\end{align}
$$
したがって、
h_{k}[n] = 2\ p_{0}[n]\cos{\left(\frac{\pi}{M}\left(k+\frac{1}{2}\right)\left(n-\frac{N}{2}\right)+\theta_{k}\right)} \tag{1}
$$
が求められます。
また、\(f_{k}[n]=h_{k}[N-n]\ \) より、
f_{k}[n] = 2\ p_{0}[n]\cos{\left(\frac{\pi}{M}\left(k+\frac{1}{2}\right)\left(n-\frac{N}{2}\right)-\theta_{k}\right)} \tag{2}
$$
が求められます。
おわりに
本記事では、MP3のフィルタバンクであるコサイン変調フィルタバンクの導出について説明いたしました。導出が長かったと思いますが、参考になれば幸いです。
次回についてはMP3のフィルタバンクを実装したいと思います。
■参考文献
[1] P.Vaidyanathan, "マルチレート信号処理とフィルタバンク," 科学技術出版, 2002.