独立成分分析(ICA)による音源分離を試してみました。独立成分分析はマルチチャネルの音源分離では代表的な方法ではないかと思います。その理由としては音源に関する情報をほとんど持っていなくても音源分離(ブラインド信号源分離)できる点にあります。
本記事では、独立成分分析の中でも単純な方法で音源分離をしてみました。
独立成分分析
独立成分分析では、音源信号が統計的に独立であると仮定して、各分離信号の独立性が最大となるように音源を分離します。
\(x\) と \(y\) が独立とは、\(y\) の値が得られたとしても \(x\) に関する情報が何も得られないときのことをいいます。
一応、参考文献[1] の独立についての数学的な説明は以下です(私は上手く飲み込めていないですが...)。
確率密度 \(x\) と \(y\) とが独立であるとは、
$$
p_{x,y}(x,y) = p_x(x) p_y(y)
$$が成立することである。すなわち、\(x\) と \(y\) との密度関数 \(p_{x,y}(x,y)\) がそれぞれの周辺分布 \(p_x(x)\) と \(p_y(y)\) の積に因数分解できるということである。
独立性が高いかどうかは、その信号の分布がガウス分布より離れている(非ガウス性が高い)かどうかでわかります。
これは中心極限定理によって独立な確率変数の和の分布はガウス分布に近づくので、逆にガウス分布から離れていれば独立性が高いからです。
混合した音声が本当にガウス分布に近づくかどうか自分でも確かめてみましたが、本当に以下のようにガウス分布に近づきます(赤線はガウス分布、N は音源数)。
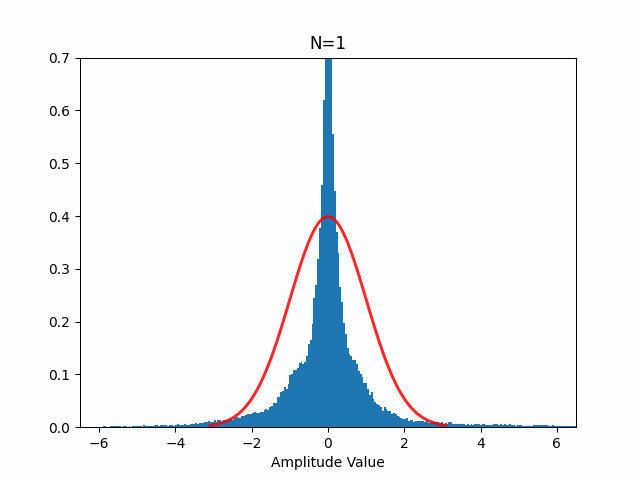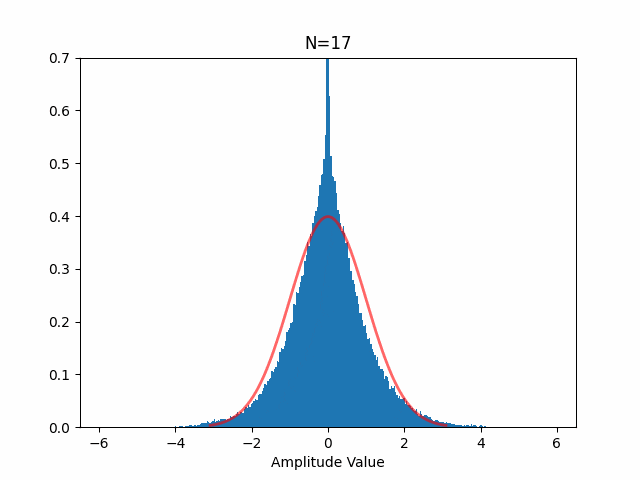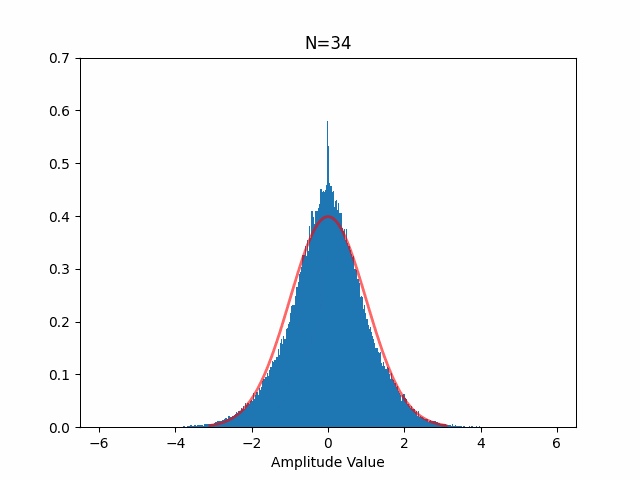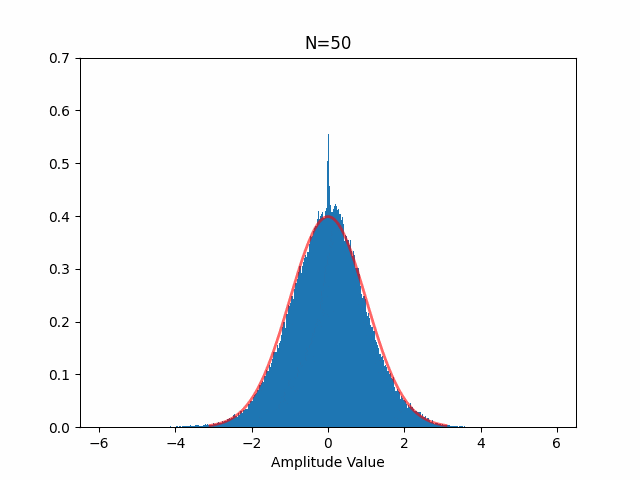
独立成分分析のやり方
独立成分分析では、以下のように混合されたとき
$$
\begin{equation}
\begin{bmatrix}
x_{1}[n] \\
x_{2}[n] \\
\vdots \\
x_{M}[n]
\end{bmatrix}
= {\mathbf A}
\begin{bmatrix}
s_{1}[n] \\
s_{2}[n] \\
\vdots \\
s_{M}[n]
\end{bmatrix}
\end{equation}
$$
\(x_{1}[n]\cdots x_{M}[n]\) を観測して、行列 A と\(s_{1}[n]\cdots s_{M}[n]\) を求めていきます。
この問題を解くことはできないですが、独立成分分析で推定することは可能です。
大まかな独立成分分析のやり方としては以下の分離信号 \(y_{1}[n]\cdots y_{M}[n]\) の独立性が最大となるように分離行列 \({\mathbf W}\) (行列Aの逆行列)を推定します。
$$
\begin{equation}
\begin{bmatrix}
y_{1}[n] \\
y_{2}[n] \\
\vdots \\
y_{M}[n]
\end{bmatrix}
= {\mathbf W}
\begin{bmatrix}
x_{1}[n] \\
x_{2}[n] \\
\vdots \\
x_{M}[n]
\end{bmatrix}
\end{equation}
$$
独立成分分析の手順は以下です[1]。
- 観測信号の平均を0にする
- 観測信号を白色化する
- 尖度を使用した勾配法で分離行列を求める
平均を 0 にする
この後の計算式を単純にするため、以下の式で観測信号の平均を 0 にします。
$$
x = x' - {\rm E}[x']
$$
独立成分推定後は、\(A^{-1}{\rm E[x']}\) を独立成分に加えることで差し引かれた平均を復元します。
ただ、音信号の場合は 0Hz の信号は聴こえないため、個人的には復元する必要はないかなとも思います。
白色化
ICAで推定するパラメータを減らすために白色化による前処理を行います。
白色化とは、それぞれの信号を無相関にして、分散を1にすることをいいます。数式で表現すると白色化した信号 \({\mathbf z}\) の共分散行列は以下のように単位行列になります。
$$
{\rm E}[{\mathbf z}{\mathbf z}^T] = {\mathbf I}
$$
白色化の手順としては、まず共分散行列を固有値分解します。
$$
{\rm E}[{\mathbf x}{\mathbf x}^T] = {\mathbf E}{\mathbf D}{\mathbf E}^T
$$
ここで、E が固有ベクトルからなら行列、D は固有値を対角化した行列です。
次に D と E を使って
$$
\begin{align}
{\mathbf V} &= {\mathbf E}{\mathbf D}^{-1/2}{\mathbf E}^T \\[5pt]
{\mathbf z} &= {\mathbf V}{\mathbf x}
\end{align}
$$
のようにすることで白色化できます。
以上の操作で白色化できることは z の共分散行列が単位行列になることから確認できます。
$$
\begin{align}
{\rm E}[{\mathbf z}{\mathbf z^T}] &= {\mathbf V}{\rm E}[{\mathbf x}{\mathbf x}^T]{\mathbf V}^T \\[5pt]
&= {\mathbf E}{\mathbf D}^{-1/2}{\mathbf E}^T{\mathbf E}{\mathbf D}{\mathbf E}^T{\mathbf E}{\mathbf D}^{-1/2}{\mathbf E}^T \\[5pt]
&= {\mathbf I} \hspace{1em} ({\mathbf E}{\mathbf E}^T={\mathbf I})
\end{align}
$$
\({\mathbf E}\) は固有ベクトルを並べたものであるため直交行列であり、\({\mathbf E}{\mathbf E}^T={\mathbf I}\) となります。
白色化のメリットとしては推定するパラメータを減らせるというのがあります。
これは行列 \(\tilde{\mathbf A}={\mathbf V}{\mathbf A}\) が直交行列となり、要素数 N^2 を求めるところが直交行列の自由度 N(N-1)/2 だけ求めればよいためです。つまり、白色化によって独立成分分析の問題は半分解けたようなものです。
尖度を使用した勾配法
独立性の尺度はいくつかありますが、本記事では尖度の絶対値を使用します。
尖度
確率変数の平均が0の場合、尖度 kurt(y) は以下のように定義されます。
$$
{\rm kurt}(y) = {\rm E}[y^4] - 3({\rm E}[y^2])^2
$$
平均0ではない場合はもう少し複雑になります。
尖度はガウス確率変数のとき0になり、尖った分布には正の値になり、平坦な分布には負の値になります。
勾配法
まず、乱数から分離行列の初期値を作成します。
それから、分離信号 \(y_{m}\) の尖度の絶対値の勾配を求めて、その方向に分離行列の行ベクトル \({\mathbf w}_m\) を動かして行きます。
分離信号 \(y_{m}\) の尖度の絶対値の勾配は以下のように計算できます。
$$
\frac{\partial |{\rm kurt}(y_{m})|}{\partial \mathbf{w}_{m}} = 4\ {\rm sign}({\rm kurt}({\mathbf w}_{m}{\mathbf z}))\left[ {\rm E}[{\mathbf z}({\mathbf w}_{m}{\mathbf z})^3]-3{\mathbf w}_{m}||{\mathbf w}_{m}||^2\right]
$$
ここで、\({\rm sign}\) は符号関数であり、正のとき 1、負のとき -1 となります。
また、白色化したデータでは \({\rm E}[({\mathbf w}_{m}{\mathbf z})^2]=||{\mathbf w}_{m}||^2\) であり、音源信号\(s_{m}\) の分散を1 と仮定すると\(||{\mathbf w}_{m}||^2=1\) に制限されます。そのため、勾配の方向に \({\mathbf w}_{m}\) を進めた後は\(||{\mathbf w}_{m}||^2=1\)に射影する必要があります。
くわえて、勾配の式のカッコ内の最後の項 \(-3{\mathbf w}_{m}||{\mathbf w}_{m}||^2\) については \({\mathbf w}_{m}\) のノルムを変えるだけのため省略できることに注意すれば、勾配法は最終的に次のようになります。
$$
\begin{align}
\Delta {\mathbf w}_m &= \alpha \cdot \ {\rm sign}({\rm kurt}({\mathbf w}_{m}{\mathbf z}))\ {\rm E}[{\mathbf z}({\mathbf w}_{m}{\mathbf z})^3] \tag{A}\\[5pt]
{\mathbf w}_m &\leftarrow {\mathbf w}_m + \Delta {\mathbf w}_m^T \tag{B} \\[5pt]
{\mathbf w}_m &\leftarrow {\mathbf w}_m/||{\mathbf w}_m|| \tag{C}
\end{align}
$$
ここで、\(\alpha\) は 学習係数 です。
直交化
1つの独立成分だけ推定する場合は上記のやり方でよいですが、複数の独立成分を推定する場合は他の行ベクトルが同じベクトルに収束しないように毎反復後に\({\mathbf w}_1,\cdots,{\mathbf w}_M\) を直交化する必要があります。
本記事では、グラムシュミットの方法を用いた逐次的直交化を使用します。
逐次的直交化では p 個のベクトル \({\mathbf w}_{1},\cdots,{\mathbf w}_{p-1}\) が求まっているとき、\({\mathbf w}_{p}\) を更新後、すでに求まった p-1 個のベクトルへの射影を引き、\({\mathbf w}_{p}\) を正規化します。
具体的には以下の手順となります。
- (A)式と(B)式で \({\mathbf w}_{p}\) を更新
- 以下の式で直交化を行う
$$
{\mathbf w}_{p} \leftarrow {\mathbf w}_{p}-\sum_{j=1}^{p-1} ({\mathbf w}_p {\mathbf w}_j^T) {\mathbf w}_j
$$ - \({\mathbf w}_{p}\) を(C)式で正規化する
- \({\mathbf w}_{p}\) が収束していなければ 1 に戻り、収束していれば \({\mathbf w}_{p+1}\) を求める。
プログラム
ソースコード
独立成分分析(尖度を用いた勾配法)で音源分離するソースコード ica.py は以下です。
import numpy as np
import numpy.linalg as LA
import soundfile as sf
# パラメータ
wav_in1_name = "input1.wav"
wav_in2_name = "input2.wav"
wav_out1_name = "output1.wav"
wav_out2_name = "output2.wav"
ch = 2 # チャンネル数
alpha = 1e-2 # 学習係数
eps = 1e-6 # 収束判定値
# WAV を読み込む
x1, fs = sf.read(wav_in1_name)
x2, fs = sf.read(wav_in2_name)
x = np.zeros((ch, len(x1)))
x[0,:] = x1
x[1,:] = x2
# 平均をゼロにする
x -= np.mean(x, keepdims=True, axis=1)
x_power = np.mean(x**2) # x の2乗平均
# 白色化
sigma = np.cov(x, bias=True)
d, E = LA.eigh(sigma)
D = np.diag(d**(-1.0/2.0)) # D**(-1/2)
V = E @ D @ E.T
z = V @ x
z_power = np.mean(z**2) # z の2乗平均
# 尖度を用いた勾配法
W = np.zeros((ch,ch))
for j in range(ch):
w_j = np.random.rand(1,ch) # 乱数で初期化
w_j = w_j / LA.norm(w_j) # 正規化
while True:
w_j_pre = w_j
# 勾配法による更新
delta_w = alpha * np.mean((z * (w_j @ z)**3), keepdims=True, axis=1)
w_j = w_j + delta_w.T # 更新
# 直交化
for i in range(j):
w_j -= (w_j @ W[i:i+1,:].T)*W[i:i+1,:]
# 正規化
w_j = w_j / LA.norm(w_j)
# 収束判定
print("w_j - w_j_pre = %f" % LA.norm(w_j - w_j_pre))
if LA.norm(w_j - w_j_pre) < eps:
W[j:j+1,:] = w_j
break
# 音源分離
y = W @ z
y = np.sqrt(x_power/z_power) * y
print(W)
# WAVファイルを書き込む
sf.write(wav_out1_name, y[0,:], fs, subtype='PCM_16')
sf.write(wav_out2_name, y[1,:], fs, subtype='PCM_16')
11~12行目:学習係数と収束判定値は何回か実行して上手くいったものを載せています。
22行目:観測信号の平均を 0 にしています。このソースコード内では差し引かれた平均の復元はしていないです。
42行目:(A)式の計算をしています。sign の計算をしていないのは音源として音声などの優ガウス分布のものを取り扱うため、その計算を省略しています。
60行目:分離信号の分散が 1 となっていて、音量がでかすぎるため、分離信号の平均パワーを観測信号の平均パワーとなるようにしています。
実行方法
(1) プログラムを実行するディレクトリにソースコード(ica.py)と2つの入力 WAV データを格納する。
(2) ソースコード5~12行目の入力データ名とパラメータを修正する。
# パラメータ
wav_in1_name = "input1.wav"
wav_in2_name = "input2.wav"
wav_out1_name = "output1.wav"
wav_out2_name = "output2.wav"
ch = 2 # チャンネル数
alpha = 1e-2 # 学習係数
eps = 1e-6 # 収束判定値
(3) 以下のコマンドで python を実行することで、 音源分離のデータが出力される。
$ python ica.py音源分離の結果
以下の混合行列で2つの音声を混合して、独立成分分析で分離できるか確かめてみました。
$$
\begin{equation}
{\mathbf A} =
\begin{bmatrix}
0.4 & 0.8 \\
0.8 & 0.24
\end{bmatrix}
\end{equation}
$$
混合前の音声は以下です。
女性音声 s1
男性音声 s2
混ぜた音は以下です。
観測信号 x1
観測信号 x2
独立成分分析で音源分離した音声は以下になります。
分離信号 y1
分離信号 y2
おわりに
本記事では、独立成分分析による音源分離を試してみました。想像以上に上手くいったので驚いています。
独立成分分析のやり方は今回紹介した方法以外にもありますので、他の方法も試してみたいなと思います。FAST ICA とか試してみたいですね。あとは残響がある場合、独立成分分析が有効かどうかも確かめてみたいと思います。
参考文献
[1] Aapo Hyvarinen・Juha Karhunen・Erkki Oja, ”独立成分分析”, 東京電機大学出版局, 2005.
■使用した音声について
この記事で使用した音声は Mozilla Foundation で提供されている音声を使用させていただきました。
【音声のページ】
・ "Common Voice: A Massively-Multilingual Speech Corpus" 2020 Mozilla Foundation (Licensed under CC-0) https://huggingface.co/datasets/mozilla-foundation/common_voice_14_0

