本記事では、ダウンサンプリングとアップサンプリングについて説明します。
ダウンサンプリングはサンプリングレートを低くする処理で、アップサンプリングはサンプリングレートを高くする処理となります。
ダウンサンプリング
ダウンサンプリングのブロック図は以下となります。
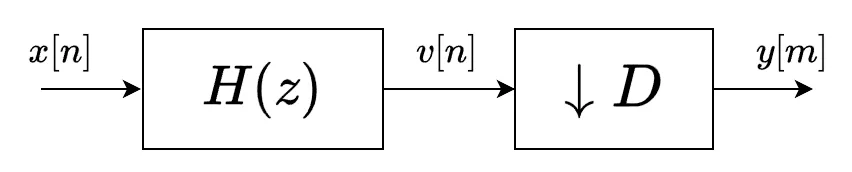
処理手順は以下です。
- デシメータのエイリアシングを回避するために入力信号を帯域制限する。
- 帯域制限された信号をD個間隔で取り出す（デシメーション）。
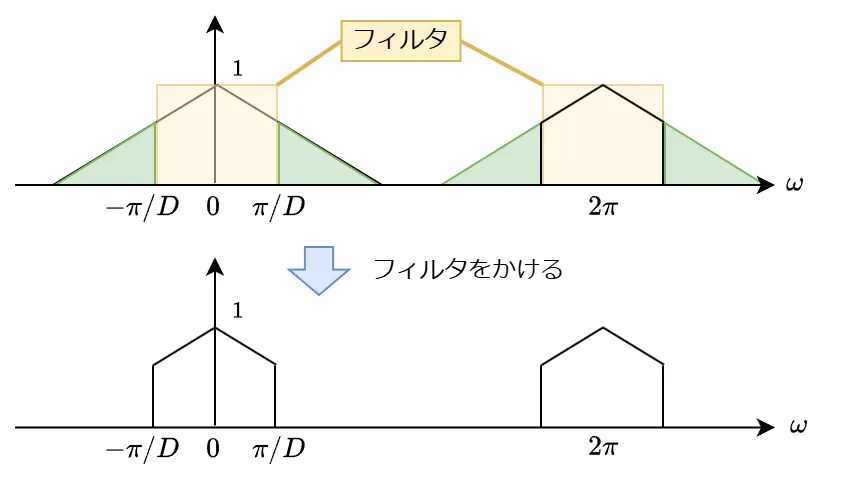
エイリアシングの回避
デシメータではサンプリングレートを下げるため、エイリアシングが生じてしまいます。エイリアシングを回避するため、あらかじめ折り返される帯域をカットしておきます。
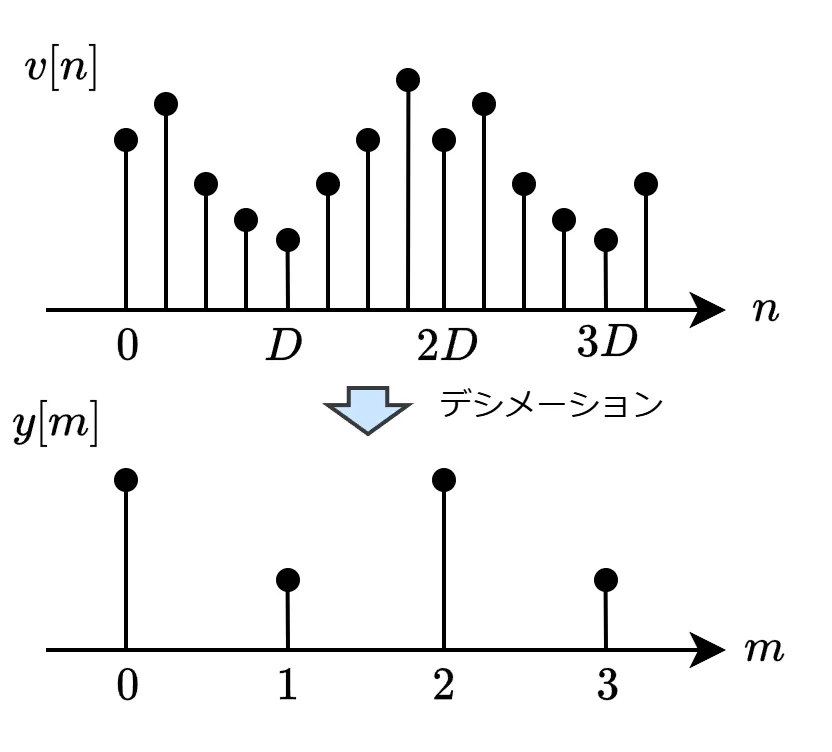
デシメーション
デシメータ（\(↓D\ \)）は信号をＤ個間隔で取り出す操作となります。
数式で表現すると以下です。
$$
y[m]=v[Dm]
$$
z変換すると以下になります。
$$
\begin{align}
Y(z)&=\sum_{m=-\infty} v[Dm]z^{-m} \\
&= \frac{1}{D}\sum_{k=0}^{D-1} V(W^{k}z^{1/D}) \tag{*}
\end{align}
$$
ここで、\(W=\exp(-j2\pi / D)\ \) です。
周波数領域では以下となります。
$$
Y(\omega)=\frac{1}{D}\sum_{k=0}^{D-1} V\left(\frac{\omega-2\pi k}{D} \right)
$$
振幅特性をグラフで表すとx軸方向にD倍拡大されて、y軸方向に1/D倍縮小され、そのグラフが\(\ 2\pi\ \)ずれて、D個並んでいるものとなります。
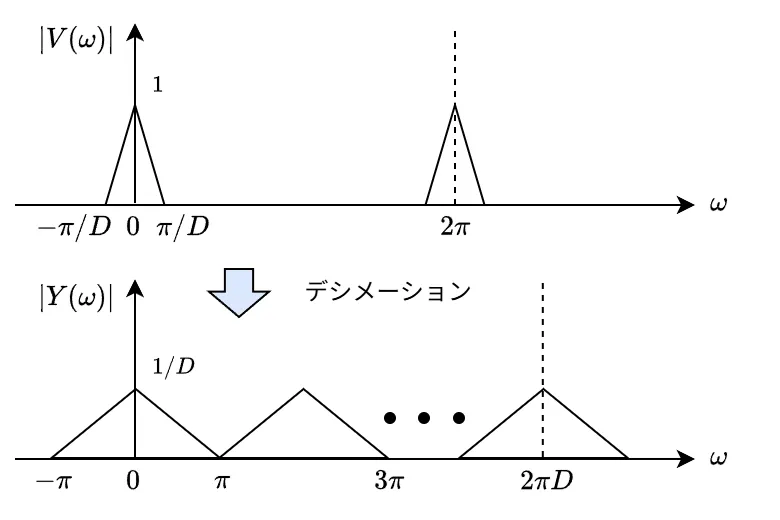
デシメーションのz変換：(*)式の求め方を補足します。
まず、インパルス列\(\ p[n]\ \) と入力信号\(\ v[n]\ \)の掛け算を計算します。
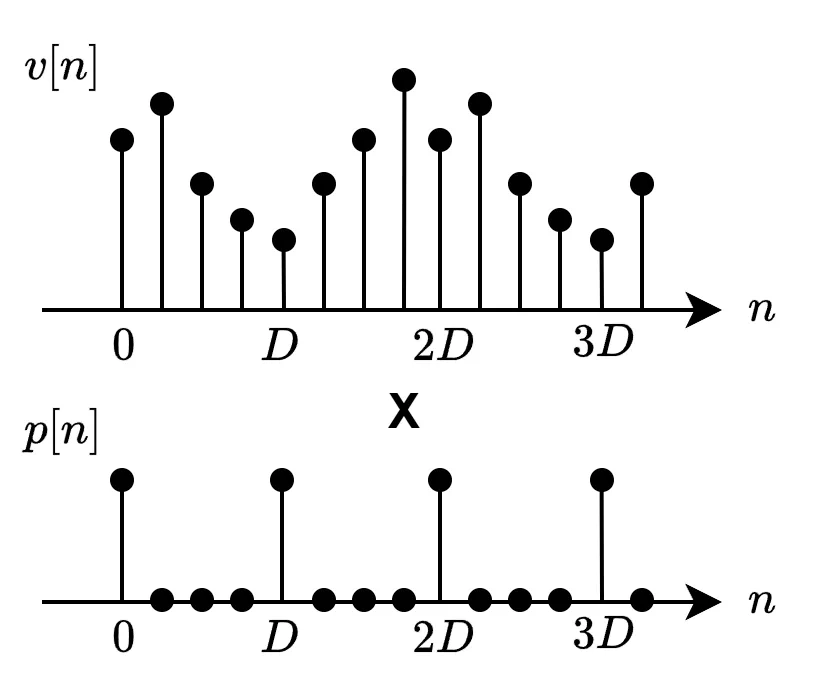
\(p[n]\ \)については離散フーリエ級数展開によって以下のように表せます。
$$
\begin{align}
p[n] &= \frac{1}{D}\sum_{k=0}^{D-1}P[k]e^{j2\pi kn/D} \\
&= \frac{1}{D}\sum_{k=0}^{D-1}1 \cdot e^{j2\pi kn/D} \\
&= \frac{1}{D}\sum_{k=0}^{D-1}e^{j2\pi kn/D}
\end{align}
$$
\(P[k]\) はフーリエ係数の求め方から以下のように計算しています。
$$
\begin{align}
P[k] &= \sum_{n=0}^{D-1} p[n]e^{-j2\pi kn/D} \\
&= p[0] \cdot e^{-j2\pi k 0/D} \\[5pt]
&= 1
\end{align}
$$
以上より、インパルス列の掛け算のz変換は以下となります。
$$
\begin{align}
& \sum_{n=-\infty}^{\infty} p[n]v[n] z^{-n} \\
=& \sum_{n=-\infty}^{\infty} \left(\frac{1}{D}\sum_{k=0}^{D-1} e^{j2\pi kn/D}\right) v[n] z^{-n} \\
=& \frac{1}{D} \sum_{k=0}^{D-1} \left(\sum_{n=-\infty}^{\infty} v[n] (e^{-j2\pi k/D} z)^{-n}\right) \\
=& \frac{1}{D} \sum_{k=0}^{D-1} V(e^{-j2\pi k/D}z)
\end{align}
$$
したがって、\(p[n]=0\ (n\neq Dm)\ \)より
$$
\begin{align}
Y(z) =& \sum_{m=-\infty}^{\infty} p[Dm]v[Dm] z^{-m} \\
=& \sum_{n=-\infty}^{\infty} p[n]v[n] z^{-n/D} \\
=& \frac{1}{D} \sum_{k=0}^{D-1} V(e^{-j2\pi k/D}z^{1/D})
\end{align}
$$
効果的構成
上記の計算でダウンサンプリングが可能ですが、この方法を実直に行った場合、計算に無駄があります。
以下の青い値はデシメーションによって間引かれるため、フィルタの出力を計算する必要がありません。
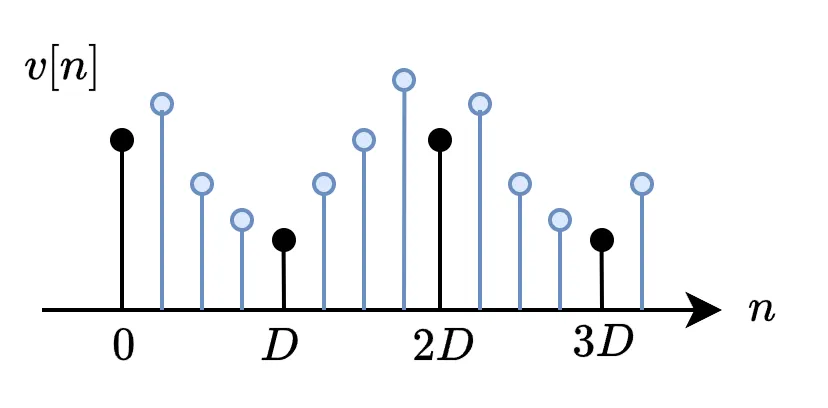
そこで、以下のようにデシメーション後にフィルタの畳み込みを計算します。
\begin{align}
y[m] &= \sum_{l=0}^{\infty} h[l]x[Dm-l] \\
&= \sum_{i=0}^{D-1} \left(\sum_{l=0}^{\infty} h[Dl+i]x[Dm-(Dl+i)] \right)
\end{align}
$$
ブロック図で表すと以下です。
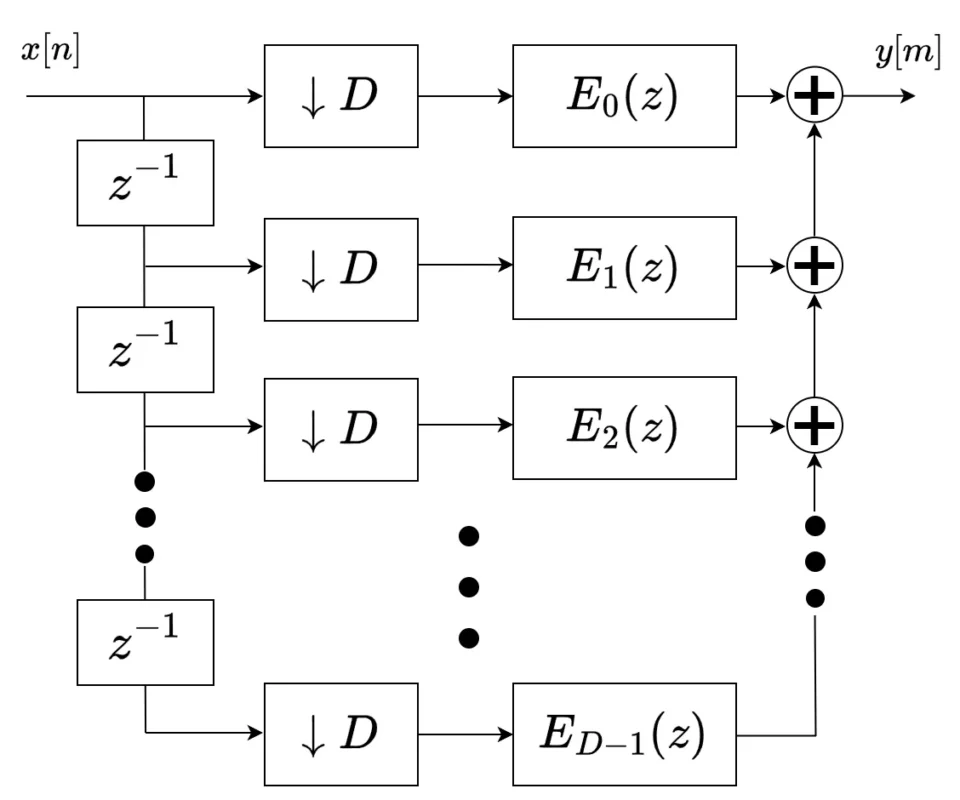
ここで、\(E_{i}(z)\ \)は伝達関数\(\ H(z)\ \)を以下のように分解したフィルタです。
\begin{align}
H(z) &= \sum_{n=-\infty}^{\infty} h[n]z^{-n} \\
&= \sum_{i=0}^{D-1} \left(\sum_{l=-\infty}^{\infty}h[Dl+i]z^{-Dl}\right) z^{-i} \\
&= \sum_{i=0}^{D-1} E_{i}(z^{D})z^{-i} \\
\Bigl(E_{i}(z) &= \sum_{l=-\infty}^{\infty}h[Dl+i]z^{-l}\Bigr)
\end{align}
$$
この伝達関数の表現をタイプⅠのポリフェーズ表現といい、\(E_{i}(z)\ \)は\(\ H(z)\ \)のポリフェーズフィルタといいます。
アップサンプリング
アップサンプリングのブロック図は以下となります。
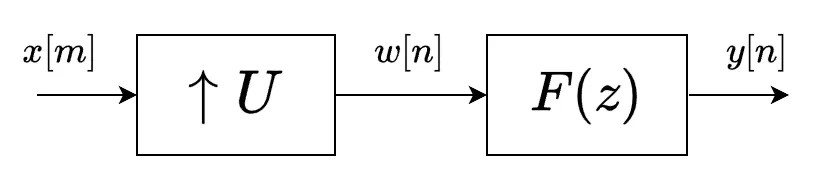
処理手順は以下です。
- 各信号間にU-1個のゼロ値を挿入する（インタポレーション）。
- インタポレーションによるイメージング成分をフィルタで除去する。
インタポレーション
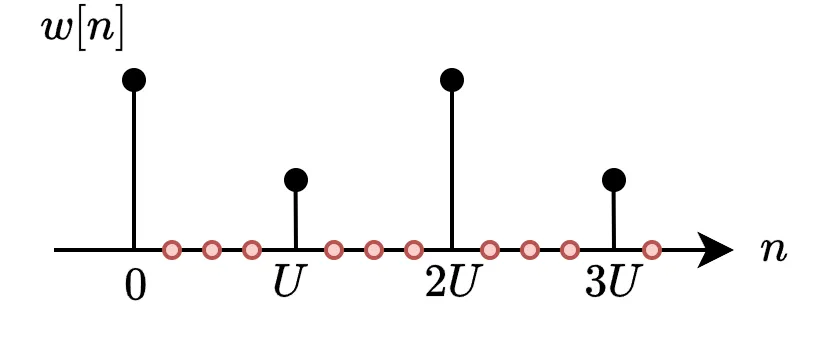
時間領域において、インタポレータ（\(↑U\ \)）は各信号間にU-1個のゼロ値を挿入する操作となります。
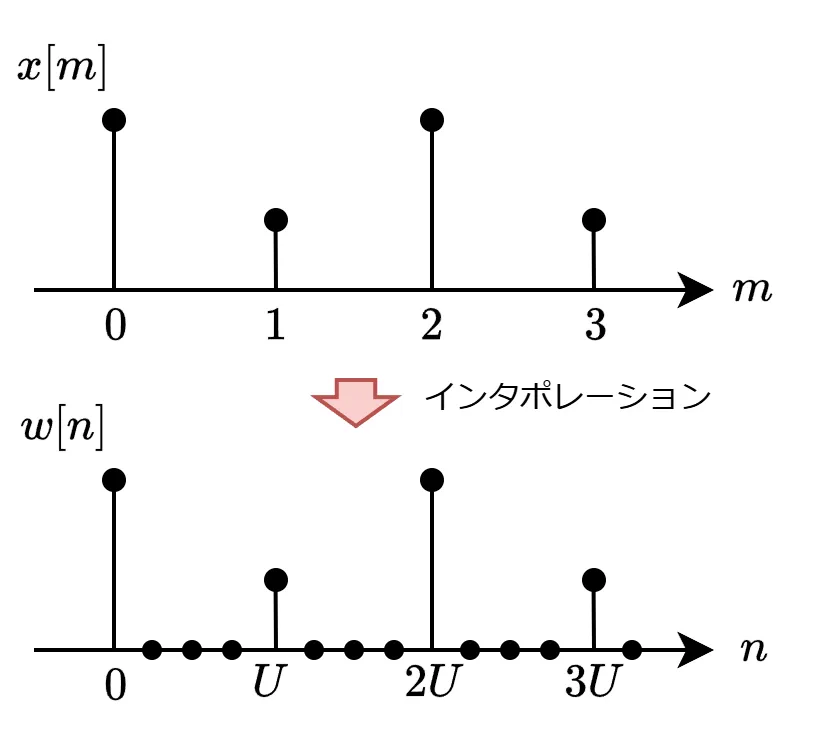
これを数式で表すと以下になります。
w[n] =
\begin{cases}
x[n/U], & n=0, \pm U, \pm 2U, \cdots \\[5pt] 0, & {\rm otherwise}
\end{cases}
$$
z変換すると以下になります。
\begin{align}
W(z) &= \sum_{n=-\infty}^{\infty} w[n]z^{-n} \\
&= \sum_{m=-\infty}^{\infty} w[mU]z^{-mU} \\
&= \sum_{m=-\infty}^{\infty} x[m]z^{-mU} \\[5pt] &= X(z^{U})
\end{align}
$$
周波数領域では以下となります。
$$
W(\omega) = X(U\omega)
$$
振幅特性をグラフで表すとx軸方向に1/U倍縮小されたグラフになります。
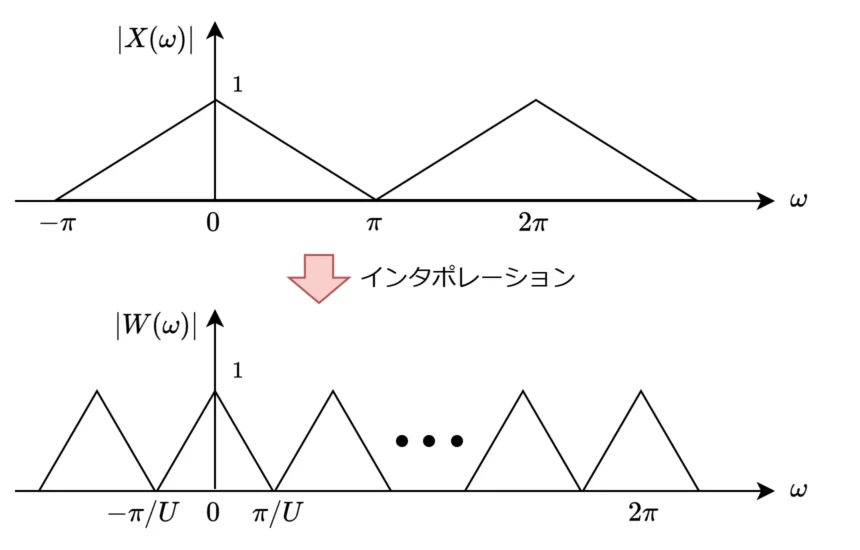
イメージング成分の除去
インタポレーションによってイメージング成分が生じているため、これを下図のようにフィルタによって除去します。
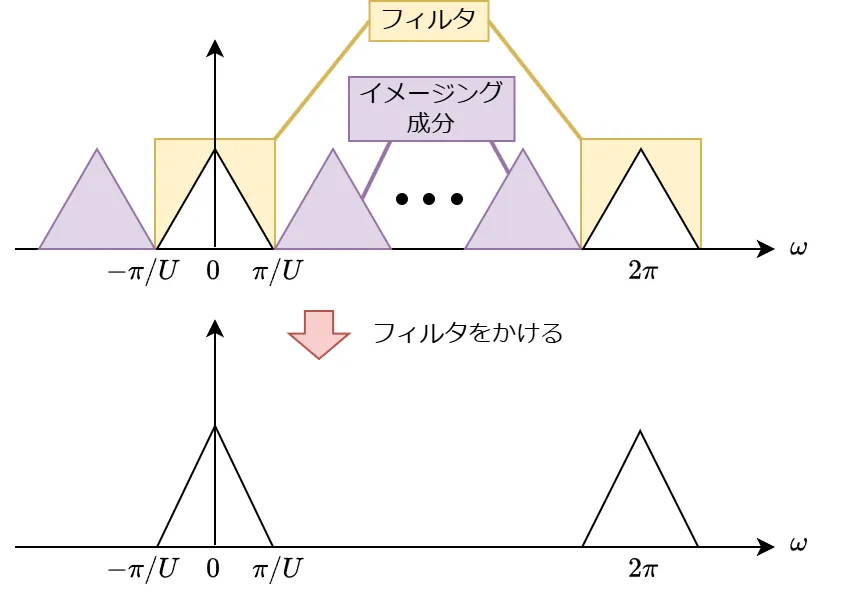
以上がアップサンプリングの処理となります。
効果的構成
アップサンプリングについても計算を効率化する方法があります。
以下の赤い値はゼロであるため、フィルタを畳み込むとき計算する必要がありません。
そこで、以下のようにアップサンプリング前に畳み込みを計算します。
y[Um+(U-1-i)] = \sum_{l=0}^{\infty} f[Ul+(U-1-i)]x[m-l] $$
ここで、\(i=0,1,\cdots,U-1\) です。
ブロック図で表すと以下です。
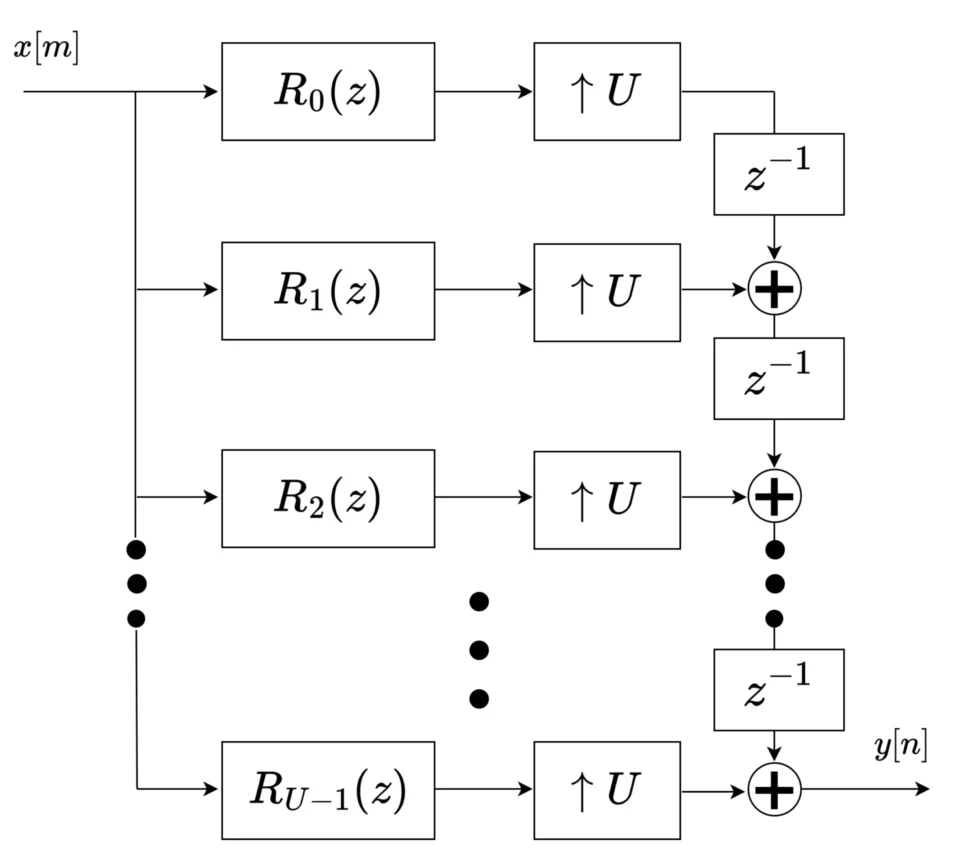
ここで、\(R_{i}(z)\) は伝達関数\(\ F(z)\ \)を以下のように分解したフィルタです。
\begin{align}
F(z) &= \sum_{n=-\infty}^{\infty} f[n]z^{-n} \\
&= \sum_{i=0}^{U-1} \left(\sum_{l=-\infty}^{\infty}f[Ul+(U-1-i)]z^{-Ul}\right) z^{-(U-1-i)} \\
&= \sum_{i=0}^{U-1} R_{i}(z^{U})z^{-(U-1-i)} \\
\Bigl(R_{i}(z) &= \sum_{l=-\infty}^{\infty}f[Ul+(U-1-i)]z^{-l}\Bigr)
\end{align}
$$
この伝達関数の表現をタイプⅡのポリフェーズ表現といい、\(R_{i}(z)\ \)は\(\ F(z)\ \)のポリフェーズフィルタといいます。
タイプⅠとタイプⅡの分解についての違いはほとんどなく、単純に以下の関係があるだけです。
$$
R_{i}(z) = E_{U-1-i}(z)
$$
おわりに
本記事では、ダウンサンプリングとアップサンプリングについて解説しました。デシメーションの z 変換の導出は少しわかりにくいため、この記事が理解のお役に立てれば幸いです。